Устойчивость круговой арки

Рассмотрим арку кругового очертания, находящуюся под действием гидростатической нагрузки (рис.44).

При нагрузке, равной критической, может произойти потеря устойчивости I рода.

При этом форма потери устойчивости может оказаться симметричной (рис. 44 а) или кососимметричной (рис. 44 б).

Рис.44

Опыты показывают, что наиболее опасной является кососимметричная форма потери устойчивости.

Круговая арка радиусом R, с центральным углом 2 и с постоянной жесткостью ЕJ упруго защемлена на опорах r₁₁ – реактивный момент, возникающий в упругой заделке от единичного поворота (=1). Пусть при критической радиальной нагрузке q_kp ось арки приняла новую изогнутую равновесную форму (кососимметричную). Дифференциальное уравнение изгиба бруса кругового очертания имеет вид:

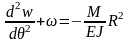(72)

w - прогиб в произвольном сечении;

 - угловая координата, отсчитываемая от оси симметрии;

М – изгибающий момент в сечении в деформации состоянии

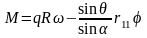
Подставив это выражение М в (72), получим

Вводим обозначения

(73)

и дифференциальное уравнение примет вид:

и решение

(74)

Для определения неизвестных параметров А, В, с

Надо составить граничные условия

1) при =0 w=0  А=0

2) при = w=0 

3) при = , или используя (73):

Дифференцируя выражения (74) имеем

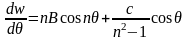
и следовательно

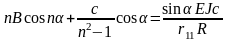
Одно из возможных решений системы этих трех уравнений это А=В=с=0.

Тогда w=0, т.е. потеря устойчивости не происходит. Ненулевое решение для А₁Вс будет:

откуда после небольших преобразований получаем уравнение устойчивости:

(75)

Определив значение n, критическую силу находим из (73)

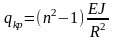(76)

Пример: Определить критическую нагрузку для арки с защемленными опорами (коэффициент жесткости r₁₁=) с радиусам R и центральны углом 2 (рис.45)

Рис.45

Из формулы (75):

или

Это уравнение решается в каждом частном случае путем подбора.

Возьмем =30⁰ ctg=1,73 n=1,73tgn

Придавая n=7 A=1,73tg(730)=1,73tg210⁰=1,730,578=1

n=8 A=1,73tg240⁰=1,751,73=3; n=9 А=

n

=8,625 A=1,73tg258⁰45=8,7 8,6258,7

Устойчивость круглых колец и труб под действием равномерной радиальной нагрузки

Если круглое кольцо находится под воздействием радиальной равномерно распределенной нагрузки, то оно (при q<q_kp) испытывает только напряжения сжатия и продольная сила равна N=qR (рис.46а). При достижения q=q_kp может произойти потеря устойчивости и кольцо примет слегка изогнутую, форму равновесия (рис.46 б)

Дифференциальное уравнение изгиба бруса кругового очертания, как было уже показано выше, имеет вид:

(77)

Изгибающий момент в произвольной точке А от действия равномерно распределенной радиальной нагрузки

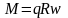(78)

а в точке А

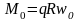
Рис.46

Подставив выражение (78) в (77) после небольшого преобразования получаем

(79)

Обозначим через , получаем общее решение однородного дифференциального уравнения

(80)

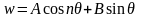(81)

Постоянные А и В находим из граничных условий:

1) при =0

откуда В=0

2) при

n0, А0, т.к. w не обращается в нуль, следовательно , что дает минимальное значение n_min=2.

Таким образом, минимальная критическая нагрузка, соответствующая данной форме потери устойчивости, определится из условия

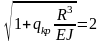или (82)

Результаты, полученные для круглого кольца, могут быть применены также при расчете на устойчивость длинных труб круглого поперечного сечения.

При этом для определения q_kp подставить вместо Е величину , где  - коэффициент Пуассона и вместо J величину , где h - толщина стенки.

Таким образом, для труб получаем:

(83)