
- •2.На какие основные виды можно подразделить управление движением, рассматривая управление манипулятором как задачу формирования траектории движения?
- •3.Как осуществляется управление манипулятором Пума?
- •4. Как осуществляется методика вычисления управляющих моментов?
- •5. Приведите эквивалентную схему двигателя постоянного тока с управлением в цепи якоря, который может быть использован в сочленениям манипулятора?
- •6.Запишите выражения для момента развиваемого на выходном валу двигателя?
- •7.Изложите метод получения передаточной функция одного сочленения робота.
- •13. Как осуществляется независимое программное управление движением?
- •14. Как осуществляется независимое программное управление движением по скорости?
- •15. Как осуществляется независимое программное управление движением по ускорению?
- •16. Как осуществляется независимое программное управление движением по силе?
- •17. Как осуществляется адаптивное управление по заданной модели
- •18. Как осуществляется независимое адаптивное управление движением?
- •19. Какие методы измерения в дальней зоне Вы знаете? Кратко опишите принцип их работы?
- •20. Как осуществляется очувствление в ближней зоне?
- •Индуктивные датчики
- •21. Какие тактильные датчики Вы знаете? Кратко опишите принцип их работы
- •Дискретные пороговые датчики
- •Аналоговые датчики
- •22. Как осуществляется силомоментное очувствление?
- •23/24. Как производиться планирование траекторий манипулятора?
- •25. Как производиться сглаживание траектории в пространстве присоединенных переменных?
- •27. Как определяется скорость точки звена манипулятора?
- •28. Как записывается кинетическая и потенциальная энергия манипулятора?
- •29. Запишите уравнения манипулятора в форме Лагранжа-Эйлера?
- •30. Какие типы управления манипуляторам Вы знаете?
- •31/32.Опишите блок-схему планировщика траекторий?
- •33.Дайте общую постановку задачи планирования траекторий?
- •34.Как производиться расчет 4-3-4 траектории?
- •35.Как производиться сглаживание траектории в пространстве присоединенных переменных?
- •36. Как производиться планирование траекторий манипулятора в декартовой системе координат?
- •41.Как осуществляется управление универсальным роботом?
- •42.Перечислите состав и конструкция унифицированных мехатронных модулей ?
- •43.Перечислите состав модулей системы управления cу уртк .
- •44.Перечислите назначение и основные характеристики системы управления уртк .
- •50.Как осуществляется тестирования системы управления?
33.Дайте общую постановку задачи планирования траекторий?
Глобальное планирование траектории робота в среде с препятствием основано, как правило, на оптимизационных методах. Полученная на основе моделирования в пространстве состояний карта столкновений позволяет решить задачу глобального планирования траектории, используя стратегию уклонения. При этом необходимо найти путь, свободный от зон столкновения, из начальной точки в пространстве состояний в конечную точку.
При постановке оптимизационной задачи необходимо найти кратчайший путь. Решение задачи уклонения в реальном масштабе времени усложняется двумя причинами: во-первых, постановка задачи, как правило, становится динамической, так как приходится рассматривать движение в окрестности препятствия с учетом неточностей, неопределенных воздействий, разброса во времени срабатывания промышленных роботов; во-вторых, из-за ограничений времени на анализ движения трудно разделить этапы обнаружения препятствий и планирования траектории по аналогии с решением задачи в режиме.
Поэтому характерным для управления в реальном масштабе времени является совмещение процедур обнаружения препятствий с локальным планированием траекторий движения. На практике это означает, что коррекция траектории движения должна осуществляться в момент первого обнаружения ближайшего препятствия до распознавания всей карты столкновений.
34.Как производиться расчет 4-3-4 траектории?
Для
определения N
траекторий присоединенных переменных
для каждого участка траектории,
воспользуемся нормированием времени
![]() .
Нормированное время изменяется от t=0
(начальный момент каждого участка) до
t=1
(конечный момент каждого участка).
.
Нормированное время изменяется от t=0
(начальный момент каждого участка) до
t=1
(конечный момент каждого участка).
Обозначения:
t– нормированное время, ;
- реальное время (сек);
![]() -
момент окончания i–го
участка траектории;
-
момент окончания i–го
участка траектории;
![]() -интервал
реального времени, затраченного на
-интервал
реального времени, затраченного на
прохождение i–го участка траектории;
![]()
![]()
![]() .
.
Траектория
движения j–й
присоединенной переменной задается в
виде последовательности полиномов
![]() :
:
![]() (1-й
участок), (14-2)
(1-й
участок), (14-2)
![]() (2-й
участок) (14-3)
(2-й
участок) (14-3)
![]() (последний
участок), (14-4)
(последний
участок), (14-4)
где i–й коэффициент j–го участка траектории рассматриваемой присоединенной переменной.
Граничные условия выбранной системы полиномов:
Начальное положение =
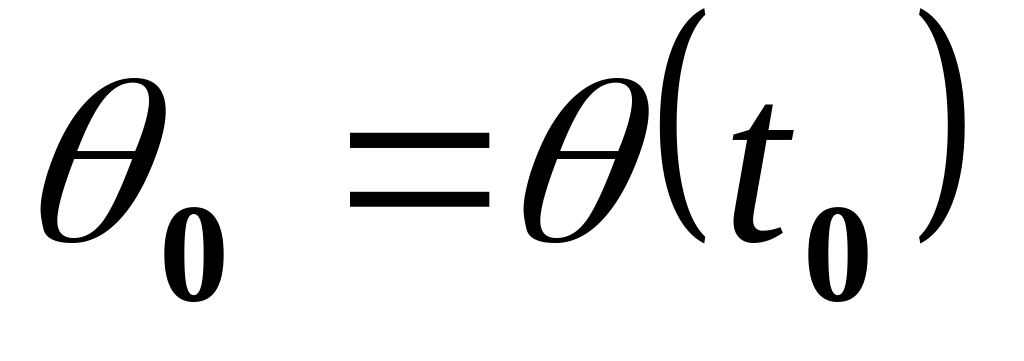 .
.Значение начальной скорости =
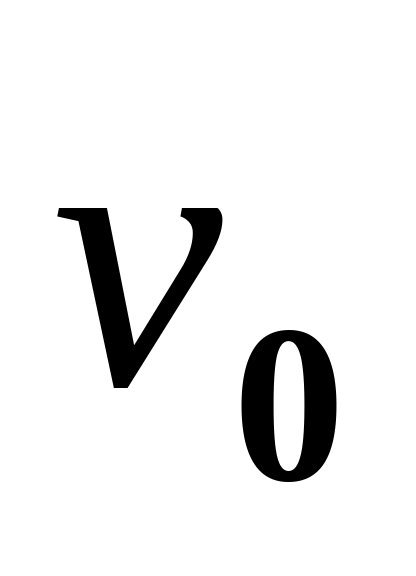 (обычно нулевое).
(обычно нулевое).Значение реального ускорения =
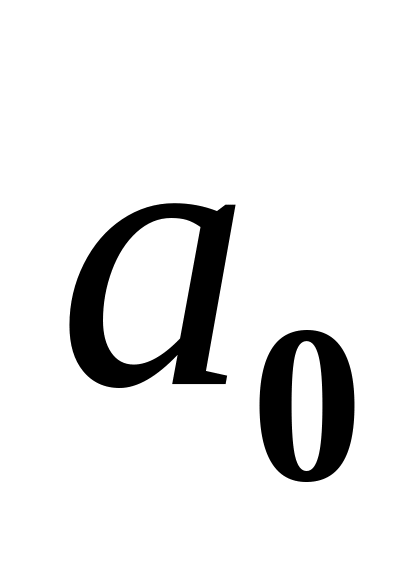 (обычно нулевое)
(обычно нулевое)Положение в точке ухода =
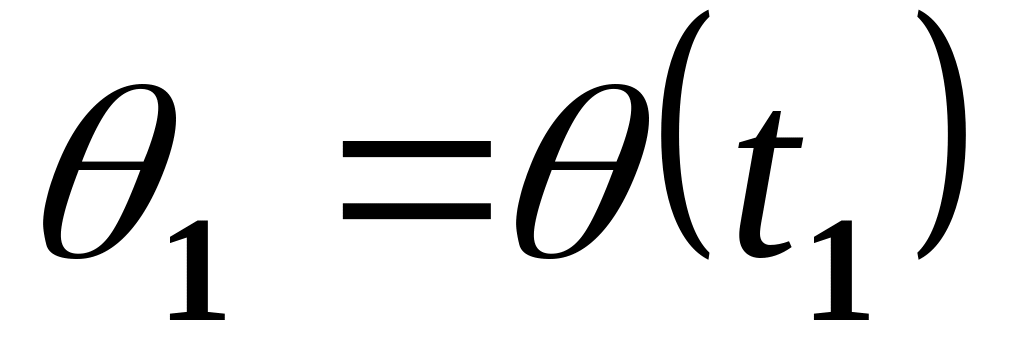 .
.Непрерывность по положению в момент
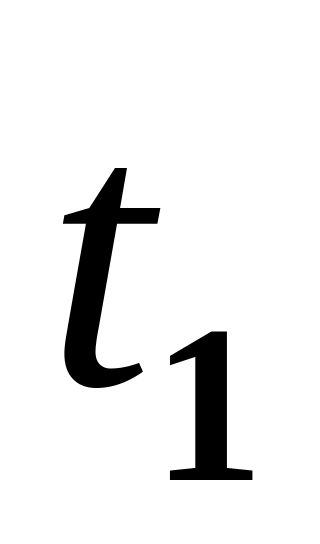 ,
т.е.
,
т.е.
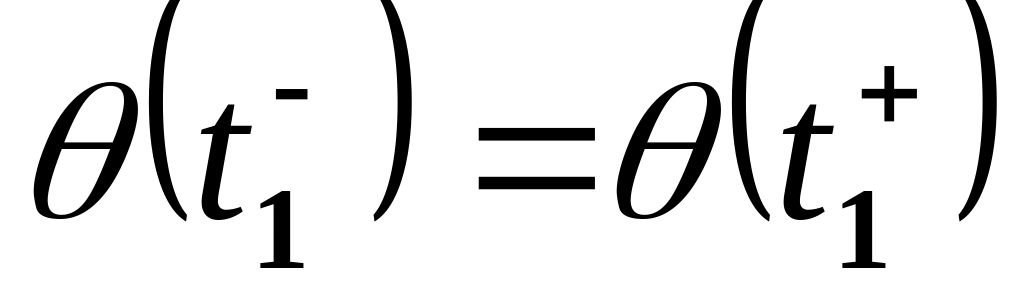 .
.Непрерывность по скорости в момент , т.е.
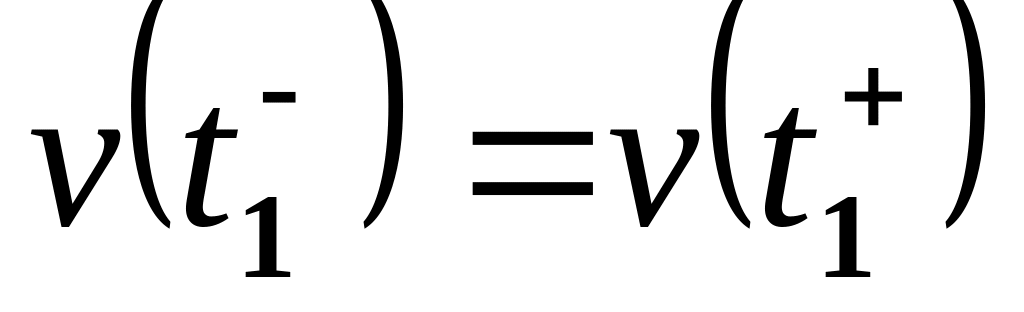 .
.Непрерывность по ускорению в момент , т.е.
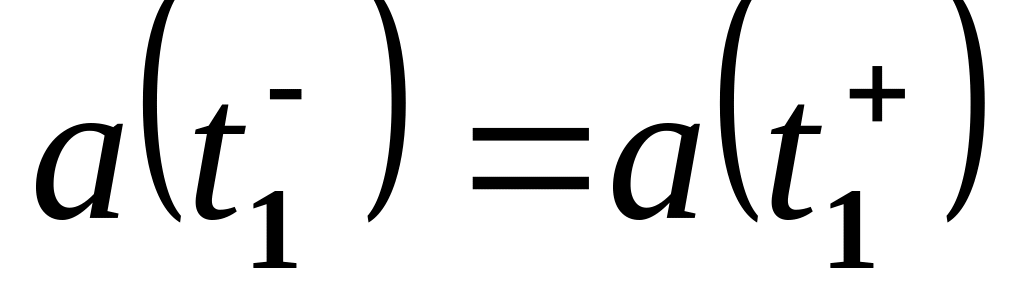 .
.Положение в точке =
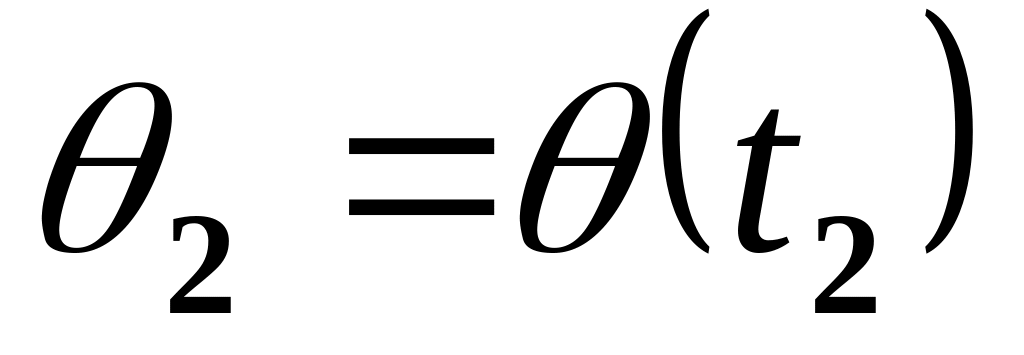 .
.Непрерывность по положению в момент
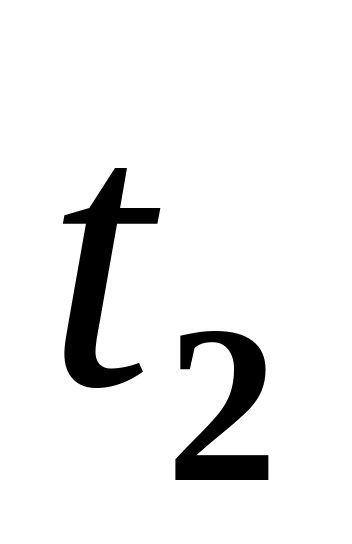 ,
т.е.
,
т.е.
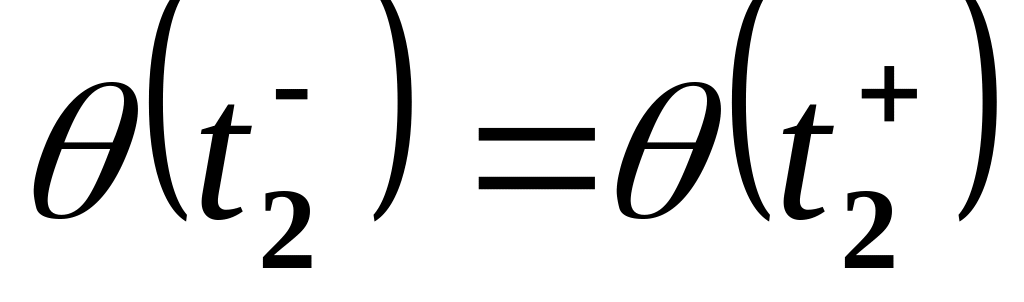 .
.Непрерывность по скорости в момент , т.е.
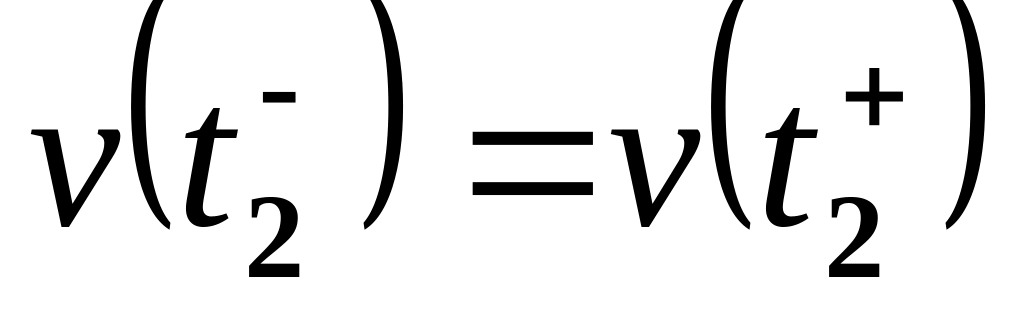 .
.Непрерывность по ускорению в момент , т.е.
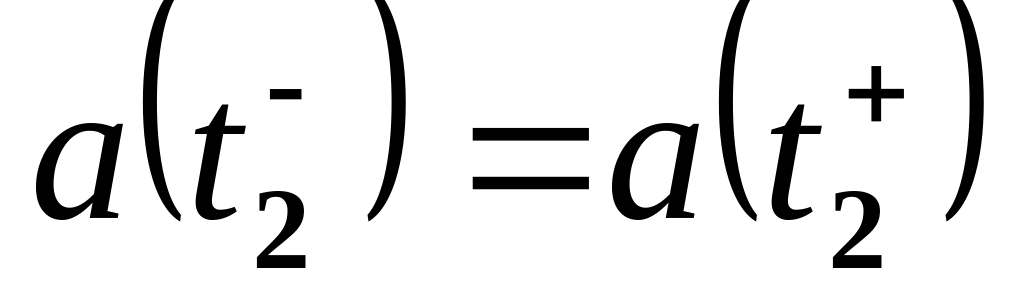 .
.Конечное положение =
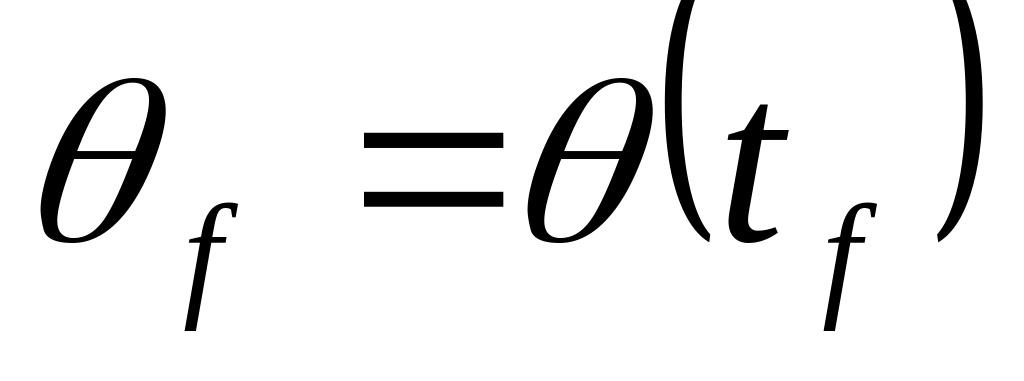
Значение конечной скорости =
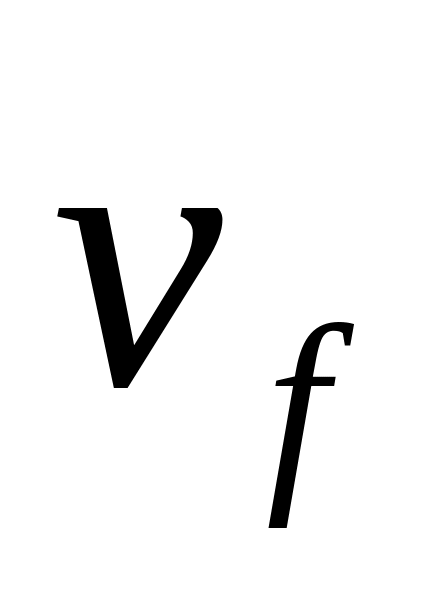 (обычно нулевое).
(обычно нулевое).Значение конечного ускорения =
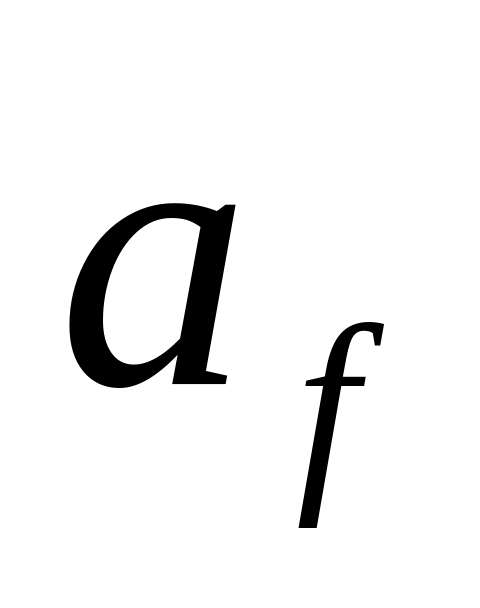 (обычно нулевое).
(обычно нулевое).
