
- •Теоретическая механика
- •Часть I
- •Содержание
- •Введение
- •1 Нормативные ссылки
- •2 Инструкция по работе с методическим указанием
- •1 Рабочая программа раздела курса «Статика»
- •2 Задание для самостоятельного решения
- •2.5 Произвольная пространственная система сил (задача с2)
- •Тема практического занятия
- •Содержание и оформление контрольной работы
- •1.14 Вопросы для подготовки к зачетам и экзаменам
- •Теоретическая механика
- •Часть 1 Статика, Кинематика
- •350072, Г. Краснодар, ул. Московская, 2, кор. А
1 Рабочая программа раздела курса «Статика»
Введение. Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. Объективный характер законов механики. Основные исторические этапы развития механики.
Литература: [1, 7-16; 5, 4-7].
Вопросы для самопроверки:
1.Какое значение имеет теоретическая механика при изучении технических наук?
2.Дайте определение курса теоретической механики.
Статика твердого тела. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные системы сил, равнодействующая, уравновешенная система сил, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей: гладкая плоскость, поверхность и опора, гибкая нить, цилиндрический шарнир (подшипник), сферический шарнир (подпятник), невесомый стержень.
Литература: [1, 16-29; 5, 7-14].
Вопросы для самопроверки:
Что изучает статика?
Чем характеризуется вектор силы?
Что называется системой сил?
Какая сила называется уравновешивающей?
Какие системы сил называются уравновешенными?
Что такое равнодействующая?
Как произвести разложение силы на составляющие?
Что называется реакцией связи?
Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое условие равновесия системы сходящихся сил. Аналитические условия равновесия пространственной и плоской систем сходящихся сил. Теорема о равновесии трех непараллельных сил.
Литература: [1, 31-43; 5, 14-35].
Вопросы для самопроверки:
Дайте определение системы сходящихся сил.
Запишите условия равновесия системы сходящихся сил в векторной, геометрической и аналитической формах.
Теория пар сил. Момент силы относительно точки (центра) как вектор. Пара сил. Момент пары сил как вектор. Теорема о сумме моментов сил, образующих пару, относительно любого центра. Теоремы об эквивалентности пар. Сложение пар, произвольно расположенных в пространстве. Условия равновесия системы пар.
Литература: [1, 43-56; 5, 36-46].
2 Задание для самостоятельного решения
Задачи на равновесие несвободного твердого тела под действием некоторой системы сил рекомендуется решать в следующем порядке:
1) выбрать твердое тело, равновесие которого требуется изучить для определения искомых величин (чаще всего определяют реакции внешних, а ряде случаев и внутренних связей наложенных на тело);
2) изобразить задаваемые силы, приложенные к твердому телу;
3) применив принцип освобождаемости от связей, мысленно отбросить связи, наложенные на твердое тело, заменив их соответствующими силами реакций связей;
4) убедиться в том, что данная задача является статически определимой, то есть количество алгебраических неизвестных не более количества составляемых уравнений равновесия;
5) на данное тело наложить оси декартовой системы координат и составить уравнения равновесия действующей на тело системы сил;
6) решив систему уравнений, составленных в предыдущем пункте, найти неизвестные величины.
7) провести проверку правильности решения задачи.
2.3 Решение типовой задачи (задача С1)
2.3.1 Условие задачи С1
Жесткая
рама (рис. 3) закреплена в точках А и В
при помощи неподвижного шарнира и
шарнирной опоры на катках или невесомого
стержня с шарнирами на концах, или жестко
(консольно) закреплена в точке А. На раму
действует пара сил с моментом М,
распределенная нагрузка интенсивностью
![]() и две силы
и две силы
![]() и
и
![]() ,
направления и точки приложения которых
указаны на рисунках. Исходные данные к
расчету приведены в таблице 2.
,
направления и точки приложения которых
указаны на рисунках. Исходные данные к
расчету приведены в таблице 2.
Необходимо определить реакции связей в точках А и В, вызываемые действующими нагрузками и выполнить проверку правильности решения задачи.
Указания.
При решении задачи необходимо учесть,
что уравнение моментов будет более
простым (содержать меньше неизвестных),
если определять моменты сил, приложенных
к телу, относительно точки, где пересекаются
линии действия двух неизвестных по
модулю сил (вычисляемых реакций связей).
При вычислении момента силы
![]() рекомендуется разложить ее на
составляющие
рекомендуется разложить ее на
составляющие![]() и
и
![]() таким
образом, чтобы плечи их моментов можно
было определить непосредственно из
рисунка, и затем воспользоваться теоремой
Вариньона:
таким
образом, чтобы плечи их моментов можно
было определить непосредственно из
рисунка, и затем воспользоваться теоремой
Вариньона:
![]() (
(![]() )
=
(
)
=
(![]() )
+
(
)
+
(![]() ).
).
2.3.2 Пример решения задачи С3
Условие задачи
Жесткая рама АВ (рис. 1,а) имеет в точке А подвижную шарнирную опору на катках, а в точке В – неподвижную шарнирную опору.
Все действующие нагрузки и размеры (в метрах) показаны на рисунке. Исходные данные:
F1 = 25 кН; F2 = 18 кН; М = 50 кНм; q = 20 кН/м.
![]() ;
;
![]() ;
;
![]() .
.
Размеры рамы указаны на рисунке (рис. 1,а).
Определить:
– реакции в точках А и В, вызываемые действующими нагрузками;
– выполнить проверку правильности решения задачи.
Решение
1. Рассмотрим равновесие рамы. Проведем координатные оси X и Y и изобразим приложенные к раме силы. Связи, наложенные на пластину,
заменяем
их реакциями
![]() ,
,
![]() ,
,
![]() (реакцию неподвижной шарнирной опоры
В изображаем двумя ее составляющими,
направленными вдоль координатных осей,
реакция шарнирной опоры А на катках
направлена перп
(реакцию неподвижной шарнирной опоры
В изображаем двумя ее составляющими,
направленными вдоль координатных осей,
реакция шарнирной опоры А на катках
направлена перп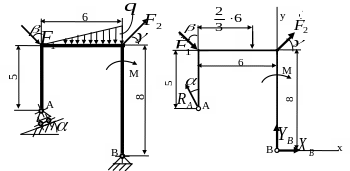 ендикулярно
опорной плоскости) (рис. 1,б).
ендикулярно
опорной плоскости) (рис. 1,б).
а) б)
Рисунок 1 – Схема к решению задачи С1
а) исходнаясхема; б) расчетная схема
2. Распределенную нагрузку интенсивностью
заменяем сосредоточенной силой
![]() ,
модуль которой равен площади эпюры
распределения, а точка приложения
расположена в ее центре тяжести. Тогда
получим :
,
модуль которой равен площади эпюры
распределения, а точка приложения
расположена в ее центре тяжести. Тогда
получим :
![]() =
=
![]() кН.
кН.

Рисунок 2 – Схема 2 к решению задачи С1
3. Силы
![]() ,
,![]() и реакцию связи
и реакцию связи
![]() разложим на составляющие, направленные
вдоль осей координат (рис. 2):
разложим на составляющие, направленные
вдоль осей координат (рис. 2):
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() .
.
4. Для полученной плоской системы сил
запишем три уравнения равновесия. При
составлении уравнения моментов в
качестве моментной точки примем точку
В, так как через эту точку проходят линии
действия двух неизвестных сил. Для
вычисление моментов сил
![]() ,
и
относительно точки В воспользуемся
теоремой Вариньона (см. выше):
,
и
относительно точки В воспользуемся
теоремой Вариньона (см. выше):
![]() = 0;
= 0;
![]() ;
(2.4)
;
(2.4)
![]() = 0;
= 0;
![]() ;
(2.5)
;
(2.5)
![]() ;
;
![]()
![]() .
(2.6)
.
(2.6)

из уравнения (2.4)
![]() из уравнения (2.5)
из уравнения (2.5)
![]()
Тогда модуль реакции в точке В найдем из соотношения:
![]()
Направление реакции в точке В найдем при помощи направляющего косинуса:
![]() =>
=>
![]() 128,450
.
128,450
.
Знаки минус указывают, что реакция
![]() и составляющая реакции
и составляющая реакции
![]() направлены противоположно показанным
на рисунках 29 и 30.
направлены противоположно показанным
на рисунках 29 и 30.
Для проверки правильности решения задачи составим уравнение суммы моментов сил, приложенных к раме. В качестве моментной рекомендуется выбрать такую точку на плоскости, через которую не проходят линии действия сил, определяемых в ходе решения данной задачи.
![]() ;
;
![]() .
(2.7)
.
(2.7)
В уравнение (2.7) подставим численные значения исходных величин и вычисленные значения реакций связей (с их знаками):
![]() .
.
После вычисления получим: 0,01![]() 0.
0.
Следовательно, задача решена правильно.
1
|
2 |
3
|
|
|
|
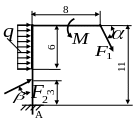
Рисунок 3- Расчетные схемы к задаче С1
7
|
8 |
9
|
10 |
|
12 |
Рисунок 3- Продолжение
|
14 |
15
|
16 |
|
|
Рисунок 3- Продолжение
19
|
|
21
|
|
23
|
|
Рисунок 3- Продолжение
25
|
|
|
|
|
30 |
Рисунок 3- Продолжение
Таблица 1 – Исходные данные к задаче С1
Номер варианта |
F1, Н |
F2, Н |
град. |
град. |
М, Нм |
q, Н/м |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
20 |
30 |
45 |
60 |
15 |
4 |
2 |
40 |
20 |
30 |
45 |
5 |
4 |
3 |
5 |
15 |
60 |
30 |
10 |
4 |
4 |
10 |
20 |
30 |
45 |
25 |
4 |
5 |
10 |
40 |
45 |
60 |
24 |
2 |
6 |
36 |
20 |
45 |
30 |
10 |
5 |
7 |
15 |
30 |
30 |
45 |
24 |
2 |
8 |
16 |
24 |
30 |
60 |
30 |
4 |
9 |
14 |
26 |
45 |
60 |
35 |
2 |
10 |
15 |
25 |
30 |
45 |
30 |
5 |
11 |
24 |
40 |
60 |
30 |
36 |
4 |
12 |
16 |
24 |
60 |
30 |
20 |
5 |
13 |
20 |
16 |
45 |
30 |
30 |
3 |
14 |
25 |
20 |
45 |
60 |
32 |
5 |
15 |
40 |
15 |
45 |
60 |
32 |
4 |
16 |
35 |
20 |
45 |
30 |
10 |
2 |
17 |
32 |
16 |
45 |
60 |
12 |
5 |
18 |
10 |
40 |
30 |
60 |
16 |
3 |
19 |
24 |
20 |
45 |
60 |
12 |
4 |
20 |
15 |
35 |
45 |
60 |
12 |
5 |
21 |
16 |
32 |
45 |
60 |
12 |
4 |
22 |
10 |
40 |
30 |
45 |
18 |
5 |
23 |
5 |
25 |
45 |
30 |
24 |
6 |
24 |
16 |
30 |
30 |
45 |
25 |
6 |
25 |
12 |
20 |
60 |
45 |
30 |
6 |
26 |
20 |
35 |
45 |
60 |
28 |
6 |
27 |
10 |
25 |
45 |
30 |
25 |
2 |
28 |
14 |
30 |
30 |
45 |
24 |
4 |
29 |
10 |
24 |
45 |
30 |
20 |
3 |
30 |
15 |
25 |
60 |
45 |
15 |
5 |




 4
4  5
5 6
6



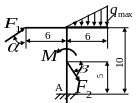 11
11
 13
13


 17
17 18
18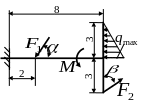
 20
20
 22
22
 24
24
 26
26 27
27 28
28 29
29