14. Мутанты в популяции

Рассмотрим некоторый ограниченный ареал, в котором обитают два вида. Пусть и N₂(t)—их численности.

Так как запасы пищи не безграничны, то выедание ее приведет к голоданию и, это ес­тественно предположить, к уменьшению скоростей роста популя­ций. Пусть F( , N₂)—количество пищи, съедаемой представите­лями обоих видов за единицу времени. Характер этой функции ясен. Она должна стремиться к плюс бесконечности при неогра­ниченном росте хотя бы одного аргумента и стремиться к нулю, когда оба аргумента стремятся к нулю.

Математическая модель этой биологической системы была записана Вольтерром:

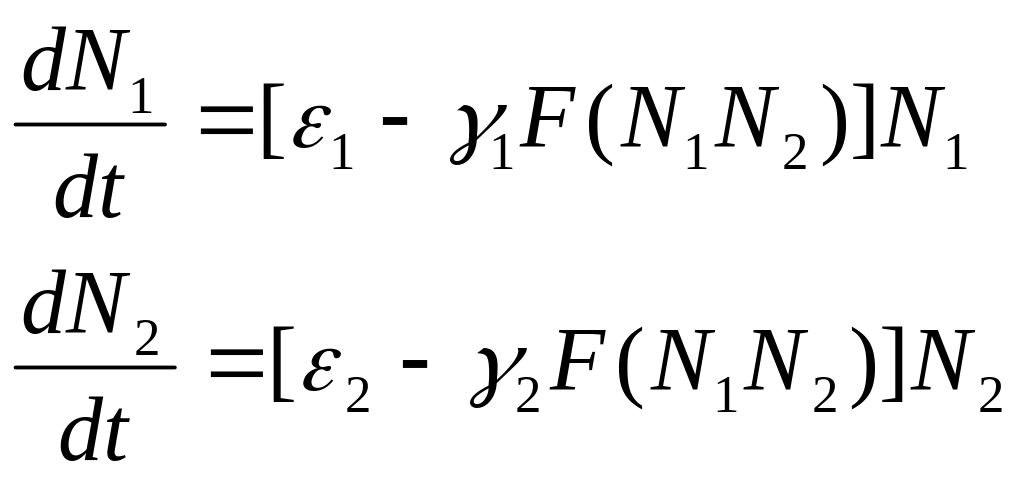
Коэффициенты называются коэффициентами чувствитель­ности к недостатку корма.

Функция F обладает следующими свойствами:

1)

2)

Из этого следует, что если и будут достаточно большими, то . А это значит, что остается ограниченным, точно также и .

При , функция стабилизируется, стремясь к .

Итак, при любых начальных данных вид, у которого отношение больше, выживет и стабилизируется, вид с меньшим отношением вымирает.

Представим себе, что у нас имеется только один вид с некоторым отношением . В какой-то момент случайно появится мутант с новым отношением , большим прежнего. Тогда сколь бы мало не было мутантов в начальный момент, со временем они вытеснят домутантную форму, а сами стабилизируются.

15. Метод Кюрасао борьбы с нежелательным видом

Сущность этого метода заключается в том, что в популяцию, которую хотят подавить (например, в популяцию сельскохозяй­ственных вредителей), регулярно вводят стерильных особей. Не участвуя в процессе естественного воспроизводства, эти особи наряду с нормальными, участвуют во внутривидовой борьбе, снижая тем самым скорость естественного увеличения популяции.

Если N (t) обозначить плотность нормальных особей, п*(t) — скорость, с которой стерильные особи вводятся в популяцию (т. е. число стерильных особей, вводимых в единицу времени на едини­цу площади), a N*(t) —плотность стерильных особей, то вопрос, на который мы хотим ответить, состоит в том, чтобы определить по возможности минимальную скорость n*(t), при которой плот­ность N (t) стремится к нулю при t->+бесконечности. (Понятно, что попу­ляция, у которой N(t) —> 0, обречена на вымирание.)