10. Рост численности популяции, подверженной отлову

Если бы не производился отлов, то скорость роста популяции была бы равна .

Но учитывая, что скорость отлова равна , то в нашем случае ( - число).

Чтобы облегчить себе задачу возьмем и конкурентные,

Тогда наша ситуация подчиняется уравнению

1. 25<v>0

X1

X1

1)

2)

3)

2. v=25

5

2. v>25

Договоримся теперь производить отлов не с постоянной скоростью, а со скоростью пропорциональной количеству, т.е. .

10-k

Отлов =

11. Логическая модель и понятие о «катастрофах»

12. Модель «хищник-жертва»

Рассмотрим некоторый ограниченный ареал, в котором обитают два вида. Пусть и N₂(t)—их численности.

Рассмотрим задачу, когда один вид является хищником по отношению к другому. Пусть ресурсы питания вида, который является жертвой, не ограничены. Обозначим чис­ленность этого вида и предположим, что в отсутствие хищника он развивался бы по экспоненте: .

Наличие хищника, разумеется, меняет вид уравнения. Пусть N₂(t) —численность хищника в момент времени t. Составляя прирост в момент t, мы должны, кроме естествен­ного прироста , учесть убыль, в силу истребления жертвы хищником. Эту убыль можно считать пропорциональной количе­ству встреч между особями обоих видов, а количество встреч пропорционально произведению . Т. О., убыль жертвы от истребления выразится величиной (где — некоторый коэффициент пропорционально­сти), а прирост за время — равенством: .

Разделив это равенство на и переходя к пределу при , получим дифференциальное уравнение . (1)

Составим теперь уравнение для численности хищника. При­рост за время будет складываться из прибыли, обуслов­ленной рождаемостью, и убыли из-за естественной смертности. Убыль можно охарактеризовать величиной . Что же касается прибыли, то для многих популяций хищников ее можно считать пропорциональной питанию, т. е. пропорциональ­ной количеству истребленной жертвы. Т. о., прибыль выразится величиной .

Разделив это равенство на и переходя к пределу при , получим второе уравнение, которое вместе с (1) образует систему 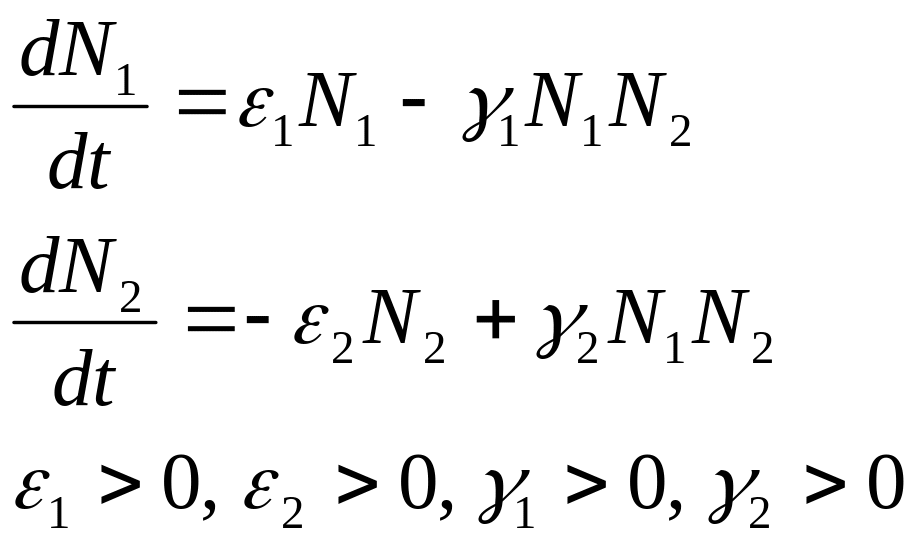(2)

Система (2) и описывает существование хищника и жертвы.

13. Модель Вольтерра для двух видов, конкурирующих за пищу

Рассмотрим некоторый ограниченный ареал, в котором обитают два вида. Пусть и N₂(t)—их численности.

Так как запасы пищи не безграничны, то выедание ее приведет к голоданию и, это ес­тественно предположить, к уменьшению скоростей роста популя­ций. Пусть F( , N₂)—количество пищи, съедаемой представите­лями обоих видов за единицу времени. Характер этой функции ясен. Она должна стремиться к плюс бесконечности при неогра­ниченном росте хотя бы одного аргумента и стремиться к нулю, когда оба аргумента стремятся к нулю.

Математическая модель этой биологической системы была записана Вольтерром:

Коэффициенты называются коэффициентами чувствитель­ности к недостатку корма.

Функция F обладает следующими свойствами:

1)

2)

Из этого следует, что если и будут достаточно большими, то . А это значит, что остается ограниченным, точно также и .

При , функция стабилизируется, стремясь к .

Итак, при любых начальных данных вид, у которого отношение больше, выживет и стабилизируется, вид с меньшим отношением вымирает.