
- •Глава 1. Определение эконометрики
- •Взаимосвязь эконометрики с другими науками
- •Понятие эконометрики
- •Типы данных и виды переменных в эконометрическом моделировании
- •Этапы эконометрического моделирования
- •1. Какое определение соответствует понятию эконометрики?
- •10. Найдите правильную последовательность этапов эконометрического моделирования:
- •Глава 2. Парная регрессия и корреляция
- •Понятие функциональной и статистической зависимостей
- •Понятие корреляционного анализа
- •Понятие корреляции
- •Различают следующие варианты корреляций:
- •Формула определения ковариации
- •Формула определения линейного коэффициента корреляции
- •Формула расчета t-критерия Стьюдента
- •Понятие регрессионного анализа
- •Уравнение линейной парной регрессии
- •Формула определения коэффициента эластичности
- •Формула определения бета-коэффициента
- •Формулы для определения t-критерия Стьюдента
- •Формула определения f-критерия Фишера
- •Формула расчета индекса корреляции
- •Понятие нелинейных моделей и их линеаризация
- •Регрессии по переменным, но линейные по оцениваемым параметрам
- •Линеаризация регрессий нелинейных по оцениваемым параметрам
- •Расчет параметров уравнения парной линейной регрессии
- •Проверка адекватности и точности модели парной линейной регрессии
- •1. Связь называется корреляционной:
- •2. По аналитическому выражению различают связи:
- •3. Регрессионный анализ заключается в определении:
- •Глава 5. Моделирование временных рядов
- •Понятие ряда динамики
- •Понятие временнóго ряда
- •Виды временны́х рядов
- •Основные требования к построению временнóго ряда
- •Понятие тренда
- •Основные виды тренда
- •Общие составляющие тренда
- •Графическое изображение составляющих тренда
- •Модели составляющих компонент
- •Характеристика параметров тренда
- •Свойства линейного тренда
- •Динамика обеспеченности жильём населения в Российской Федерации на конец года, м2
- •Показатели динамики обеспеченности жильём в Российской Федерации на конец года, м2
- •Расчётная таблица
- •Понятие о сезонных колебаниях и сезонной составляющей
- •Методы выявления сезонной компоненты
- •Динамика курса евро на ммвб в Российской Федерации, руб.
- •Расчет индекса сезонности курса евро на ммвб
- •Понятие сезонной волны
- •Динамика экспорта Российской Федерацией нефтепродуктов (по данным фтс России), млн. Тонн
- •Расчетная таблица
- •Динамика экспорта Российской Федерацией нефтепродуктов (по данным фтс России), млн. Тонн
- •Расчётные данные
- •Понятие временного лага
- •Распределение Стьюдента(t-распределение)
- •Распределение Фишера - Снедекора (f-распределение)
- •Критические точки для статистики Колмогорова Dn
Формула определения коэффициента эластичности

|
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака x на один процент |
Формула определения бета-коэффициента

|
Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину своего среднеквадратического отклонения |
После
того как уравнение регрессии построено,
выполняется проверка
его адекватности и точности.
Эти свойства модели исследуются на
основе анализа ряда остатков
![]() (отклонений расчетных значений от
фактических).
(отклонений расчетных значений от
фактических).

Корреляционный и регрессионный анализ (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии, корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенной модели.

Значения
,
соответствующие данным
![]() при теоретических значениях
и
,
являются случайными. Случайными являются
и рассчитанные по ним значения
коэффициентов
и
.
при теоретических значениях
и
,
являются случайными. Случайными являются
и рассчитанные по ним значения
коэффициентов
и
.
Проверка значимости отдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы о равенстве нулю каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных величин.
Для соответствующих коэффициентов регрессии применяют формулы.
Формулы для определения t-критерия Стьюдента

Расчетные
значения t-критерия
сравниваются с табличным значением
критерия
![]() ,
которое определяется при
,
которое определяется при
![]() степенях свободы и соответствующем
уровне значимости
.
степенях свободы и соответствующем
уровне значимости
.
|
Если расчетное значение t-критерия превосходит его табличное значение , то параметр признается значимым. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями |
Для проверки значимости уравнения регрессии в целом используется F-критерий Фишера. В случае парной линейной регрессии значимость модели регрессии определяется по формуле:
Формула определения f-критерия Фишера
|
Если
при заданном уровне значимости
расчетное значение F-критерия
с
|
Проверка наличия или отсутствия систематической ошибки (выполнения предпосылок МНК) осуществляется на основе анализа ряда остатков.

Требование |
Методы проверки требований |
Первое |
Для проверки свойства случайности ряда остатков можно использовать критерий поворотных точек (пиков). Точка считается поворотной, если выполняются следующие условия:
Далее подсчитывается число поворотных точек р. Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства:
Квадратные скобки означают, что берется целая часть числа, заключенного в скобки. Если неравенство выполняется, то модель считается адекватной
|
Второе |
Для
проверки
равенства математического ожидания
остаточной последовательности нулю
вычисляется среднее значение ряда
остатков
Если
Если
где
Значение t-критерий сравнивают с табличным . В случае, если выполняется неравенство , то модель неадекватна по данному критерию
|
Третье |
Дисперсия уровней ряда остатков должна быть одинаковой для всех значений (свойство гомоскедастичности). Если это условие не соблюдается, то имеет место гетероскедастичность. Для оценки гетероскедастичности, при малом объеме выборки, можно использовать метод Гольдфельда-Квандта, суть которого заключается в следующем: - необходимо расположить значения переменной в порядке возрастания; - разделить совокупность упорядоченных наблюдений на две группы; - по каждой группе наблюдений построить уравнения регрессии; - определить остаточные суммы квадратов для первой и второй групп по формулам:
-
рассчитать критерий
При
выполнении нулевой гипотезы о
гомоскедастичности критерий
Чем больше величина превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин
|
Четвертое |
Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью d-критерия Дарбина-Уотсона. Он определяется по формуле:
Расчетное
значение критерия сравнивается с
нижним
Возможны следующие случаи: а) если d < , то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
б)
если
Если
расчетное значение коэффициента по
модулю меньше табличного значения
в)
если
г)
если d>2,
то это свидетельствует от отрицательной
автокорреляции остатков. В этом случае
расчетное значение критерия необходимо
преобразовать по формуле:
|
Пятое |
Проверку соответствия распределения остаточной последовательности нормальному закону распределения можно осуществить с помощью R/S-критерия, который определяется по формуле:
где
Расчетное значение R/S-критерия сравнивается с табличными значениями (нижней и верхней границами данного отношения) и если значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается; в противном случае гипотеза принимается |
Для оценки качества регрессионных моделей целесообразно также использовать индекс корреляции (коэффициент множественной корреляции).




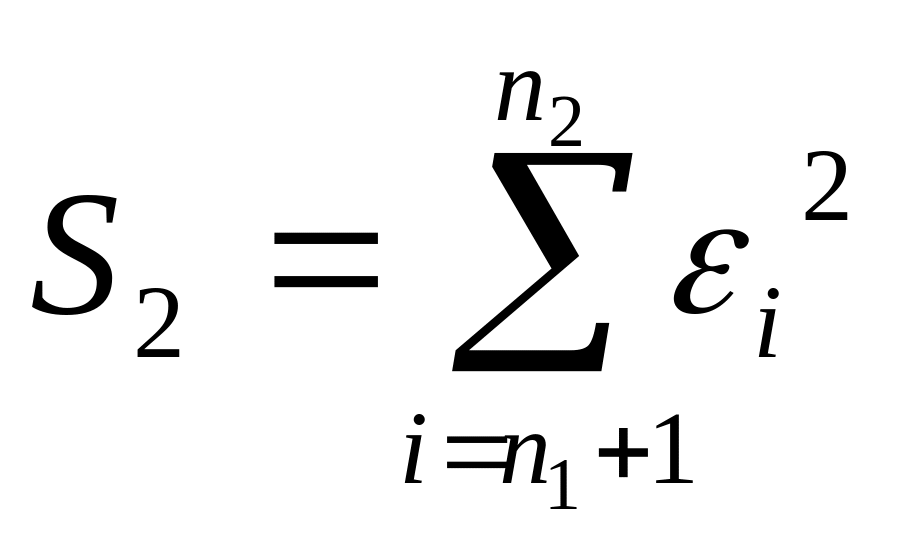
 .
.