Проверка адекватности и точности модели парной линейной регрессии
п/п |
|
|
|
|
Точки поворота |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2425 |
2027 |
398 |
158404 |
- |
- |
- |
16,41 |
2 |
2050 |
1886 |
164 |
26896 |
0 |
-234 |
54756 |
8,0 |
3 |
1683 |
1700 |
-17 |
289 |
0 |
-181 |
32761 |
1,01 |
4 |
2375 |
2431 |
-56 |
3136 |
0 |
-39 |
1521 |
2,36 |
5 |
1167 |
1350 |
-183 |
33489 |
1 |
-127 |
16129 |
15,68 |
6 |
1925 |
2017 |
-93 |
8649 |
1 |
90 |
8100 |
4,83 |
7 |
1042 |
1857 |
-815 |
664225 |
1 |
-723 |
522729 |
78,21 |
8 |
2925 |
2673 |
252 |
63504 |
1 |
1067 |
1138489 |
8,62 |
9 |
2200 |
2158 |
42 |
1764 |
0 |
-210 |
44100 |
1,91 |
10 |
1892 |
1940 |
-48 |
2304 |
1 |
-90 |
8100 |
2,54 |
11 |
2008 |
1996 |
12 |
144 |
1 |
60 |
3600 |
0,60 |
12 |
2225 |
2261 |
-36 |
1296 |
0 |
-48 |
2304 |
1,62 |
13 |
1983 |
2065 |
-82 |
6724 |
1 |
-46 |
2116 |
4,14 |
14 |
2342 |
1814 |
528 |
278784 |
1 |
610 |
372100 |
22,54 |
15 |
2458 |
2044 |
414 |
171396 |
0 |
-114 |
12996 |
16,84 |
16 |
2125 |
2606 |
-481 |
231361 |
|
-895 |
801025 |
22,64 |
Сумма |
32825 |
|
-1 |
1652180 |
8 |
|
3021007 |
191,49 |
Значимость параметров модели оценим с помощью t-критерия Стьюдента по формулам:
и
,
где
-
стандартные отклонения свободного
члена и коэффициента регрессии.
Определяются по формулам:
;
,
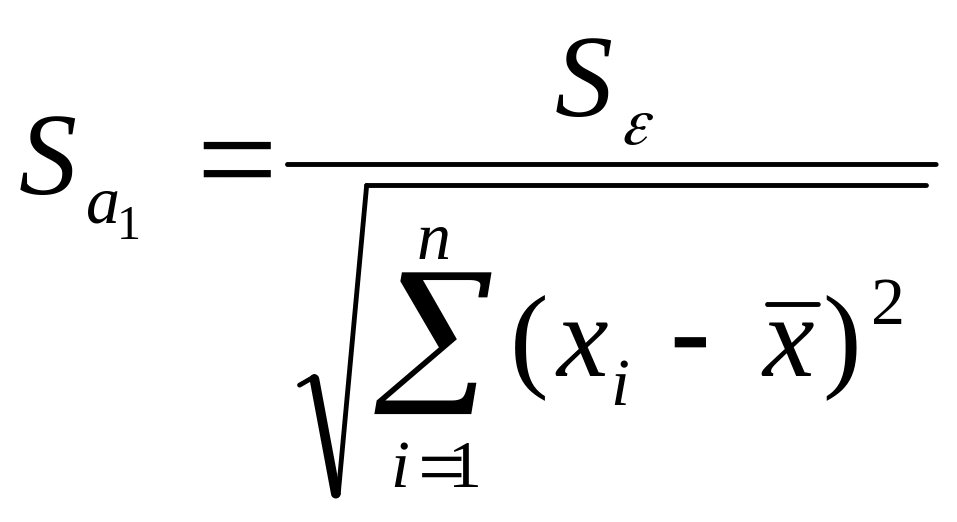Стандартное отклонение остатков модели (стандартная ошибка) определяется по формуле:
.
Значения стандартных отклонений следующие:
,
.
Расчетные значения t-критерия равны:
,
.
Табличное
значение t-критерия
с
степенями свободы и при доверительной
вероятности 0,95
равно 2,14.
Следовательно, имеем следующие результаты:
параметр
незначим;
параметр
значим.
Для проверки значимости уравнения регрессии в целом воспользуемся F-критерием Фишера.
.
Табличное
значение F-критерия
с
и
степенями
свободы и при доверительной вероятности
0,95
равно 4,60.
Так
как
,
то уравнение парной линейной регрессии
с вероятностью 0,95 в целом статистически
значимое.
4) Проверка выполнения предпосылок МНК (на основе результатов таблицы 2).
а) Проверка свойства случайности ряда остатков.
Число поворотных точек (p) равно 8.
Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства:
.
,
Неравенство
выполняется (
)
и, следовательно, модель признается
адекватной по критерию случайности.
б) Проверка равенства математического ожидания остаточной последовательности нулю.
Вычислим среднее значение ряда остатков.
.
Так как , то модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.
в) Проверка свойства гомоскедастичности.
Расположим значения факторного признака в порядке возрастания.
2293 |
2842 |
3022 |
3089 |
3135 |
3219 |
3308 |
3340 |
3357 |
3383 |
3416 |
3563 |
3724 |
3991 |
4267 |
4372 |
Разделим совокупность наблюдений на две группы и для каждой группы с помощью программы Анализ данных в EXCEL, инструмент Регрессия определим параметры уравнений регрессий и остаточные суммы квадратов.
Таблица 3
|
Уравнение регрессии |
Остаток |
1 группа |
|
|
2 группа |
|
|
Расчетный
критерий равен:
.
Табличное
значение F-критерия
с
и
степенями
свободы и при доверительной вероятности
0,95
равно 4,28.
Величина превышает табличное значение F-критерия, следовательно, свойство гомоскедастичности выполняется.
г) Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществим с помощью d-критерия Дарбина-Уотсона.
.
Расчетное
значение критерия сравнивается с нижним
и
верхним
критическими
значениями статистики Дарбина-Уотсона.
При n=16
и уровне значимости 5%,
,
.
Поскольку , то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.
д) Проверку соответствия распределения остаточной последовательности нормальному закону распределения осуществим с помощью R/S-критерия. формуле:
.
Расчетное значение R/S-критерия сравнивается с табличными значениями (нижней и верхней границами данного отношения).
Нижняя
и верхняя границы отношения при уровне
значимости
равны соответственно 3,01 и 4,09.
Расчетное значение отношения попадает в интервал между критическими границами, следовательно, с заданным уровнем значимости гипотеза о нормальности распределения принимается.
5) Оценка точности модели (таблица 2.3).
В качестве показателя точности модели используем среднюю относительную ошибку аппроксимации.
.
Уровень точности модели можно признать приемлемым.
Тесты