4. Задания для контрольных работ

1–10. На телефонной станции проводились наблюдения над числом X неправильных соединений в сутки. Результаты наблюдений представлены в виде табл. 1. Наблюдения проводились в течение 20 рабочих дней. Провести статистическую обработку результатов наблюдения, а именно:

1. составить вариационный ряд;

2. составить таблицу распределения частот и относительных частот ;

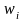3. построить полигон частот и гистограмму частостей;

4. определить выборочные характеристики средней величины: моду , медиану 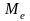, среднее значение ;

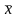5. определить выборочные характеристики неравномерности ежедневного числа неправильных телефонных соединений: размах R, дисперсию , среднее квадратическое отклонение , коэффициент вариации V;

6. записать точечные оценки генеральной средней и генеральной дисперсии.

7. составить эмпирическую функцию распределения 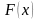ежедневного числа неправильных телефонных соединений и построить ее график.

Таблица 1

День	Число неправильных телефонных соединений за сутки
	№ варианта
	1	2	3	4	5	6	7	8	9	10
1	4	6	10	2	9	9	7	6	1	7
2	7	5	15	7	11	11	13	12	3	12
3	3	7	16	2	9	10	13	11	5	10
4	6	5	15	2	10	9	7	12	4	8
5	2	7	14	5	5	5	13	10	6	14
6	5	4	14	2	5	10	13	8	5	13
7	5	9	13	6	8	9	12	11	5	7
8	6	8	12	3	11	3	8	9	6	12
9	8	4	10	2	10	11	12	7	4	13
10	8	5	16	3	11	8	14	7	5	6
11	7	5	13	4	6	9	8	9	4	12
12	4	7	15	5	10	5	11	10	5	10
13	2	5	11	6	9	9	13	8	2	8
14	5	5	10	3	10	3	13	12	6	11
15	5	5	10	5	11	4	14	6	7	14
16	5	4	14	5	10	11	8	11	7	10
17	5	6	15	7	6	7	9	7	6	12
18	4	9	15	6	9	9	8	6	4	6
19	5	6	11	1	10	8	15	10	6	8
20	3	9	13	6	11	7	11	6	8	11

11–20. По данному (табл. 2) интервальному распределению значений признака 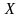некоторой выборочной совокупности необходимо:

1. построить гистограмму относительных частот;

2. найти выборочные характеристики распределения (среднее значение, моду, медиану, размах, дисперсию, среднее квадратическое отклонение, коэффициент вариации).

Таблица 2

Вариант	1		2
Номер интервала	Границы интервалов	Интервальные частоты	Границы интервалов	Интервальные частоты
1	147–155	25	50 – 62	57
2	155 – 163	39	62 – 74	73
3	163 – 171	57	74 – 86	95
4	171 – 179	68	86 – 98	88
5	179 – 187	40	98 – 110	70
6	187 – 195	21	110 – 122	67
Вариант	3		4
Номер интервала	Границы интервалов	Интервальные частоты	Границы интервалов	Интервальные частоты
1	15,6 – 17	8	35,2 – 39,2	10
2	17 – 18,4	16	39,2 – 43,2	16
3	18,4 – 19,8	33	43,2 – 47,2	46
4	19,8 – 21,2	29	47,2 – 51,2	69
5	21,2 – 22,6	22	51,2 –55,2	35
6	22,6 – 24	12	55,2 –59,2	24
Вариант	5		6
Номер интервала	Границы интервалов	Интервальные частоты	Границы интервалов	Интервальные частоты
1	51–65	37	88,4–90,0	32
2	65–79	40	90–91,6	55
3	79–93	51	91,6–93,2	65
4	93–107	58	93,2–94,8	71
5	107–121	48	94,8–96,4	48
6	121–135	36	96,4–98,0	39

Вариант	7		8
Номер интервала	Границы интервалов	Интервальные частоты	Границы интервалов	Интервальные частоты
1	0,56–0,58	67	24–28	41
2	0,58–0,60	82	28–32	59
3	0,60–0,62	106	32–36	70
4	0,62–0,64	98	36–40	63
5	0,64–0,66	77	40–44	58
6	0,66–0,68	50	44–48	39
Вариант	9		10
Номер интервала	Границы интервалов	Интервальные частоты	Границы интервалов	Интервальные частоты
1	430–490	11	7,45–8,25	33
2	490–550	16	8,25–9,05	52
3	550–610	23	9,05–9,85	76
4	610–670	27	9,85–10,65	61
5	670–730	18	10,65–11,45	49
6	730–790	15	11,45–12,25	29

21–30. По данным таблицы 2 требуется:

1. используя критерий 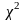-Пирсона, при уровне значимости 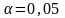проверить гипотезу о том, что случайная величина X – время, проводимое студентами в Интернете в неделю – распределена по нормальному закону, записать функцию соответствующего нормального распределения;

2. определить границы, в которых с вероятностью 0,95 заключено среднее время, проводимое студентами в Интернете в неделю;

3. определить объем выборки (число студентов, которых нужно опросить), при котором те же границы для среднего времени, проводимого студентами в Интернете в неделю, можно гарантировать с вероятностью 0,99.

31–40. Проведены исследования 200 семей некоторого района по двум показателям (признакам): Х – расходы на питание (% от общего дохода семьи); У – доходы семьи (тыс. руб.). По данным двумерной таблицы распределения (табл. 3) требуется:

1. вычислить условные средние 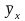, построить эмпирическую линию регрессии;

2. предполагая, что между переменными X и Y существует линейная корреляционная зависимость:

а) вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y;

б) найти уравнение прямой регрессии , построить график этой прямой на одном чертеже с эмпирической линией регрессии.

Таблица 3

1	уj	15	22	29	36	2	уj	19	23	27	31
	12	30	80				8			30	80
	20		45	20			14		55	20
	28			10	15		20	15
3	уj	21	27	33	39	4	уj	17	25	33	41
	10				25		18			15	10
	14		35	40	10		22		30	20
	18	30	60				26	45	80
5	уj	11	16	21	26	6	уj	15	20	25	30
	15	20	10				17	30	15
	20		80	45			23		85	25
	25			15	30		28			15	30
7	уj	16	20	24	28	8	уj	20	26	32	38
	20	15					24			35	30
	25	10	80	30			30			80	20
	30			45	20		36	15	20
9	уj	18	22	26	30	10	уj	23	27	31	35
	19			45	30		14	45
	24	80	10	20			21	20	10	80	30
	31	15					28			10	15