1.2.3.Графический анализ точности моделирования

Тесты проверки точности моделирования БСВ допускают графическую интерпретацию, удобную для быстрого визуального анализа качества смоделированной выборки реализаций БСВ.

В пакете СТАТМОД реализованы следующие графики:

• диаграмма рассеяния (иллюстрирует зависимость между a_i и a_t-1 ; для проверки факта наличия зависимости используется тест «ковариация»);

• гистограмма и плотность распределения (позволяет осуществить сравнительный анализ теоретического и эмпирического распределения выборки А; для проверки согласия распределения А с равномерным законом используются критерии согласия);

• график корреляционной функции с указанием доверительных границ (служит для графической поддержки теста «ковариация»);

• визуализация выборки (иллюстрирует зависимость a_i от t и может использоваться для графической поддержки критериев серий).

1.2.4.Задания

1. Осуществить моделирование n=1000 реализаций БСВ с помощью мультипликативного конгруэнтного метода (МКМ-датчика) при следующих значениях параметров датчика:

(т.е. β  {19, 259, 4099, 65539, 1048979, 16777219, 268435459})

Сравнить эти датчики по точности, используя тесты проверки точности моделирования. Найти значение m^*, при котором достигается максимальная точность моделирования.

2. Выполнить задание 1 при следующих значениях параметров датчика:

(т.е.   {5, 125, 3125, 78125, 1953125, 48828125, 1220703125})

3. Для МКМ-датчика при  = 65539 исследовать зависимость точности моделирования и величины периода Т от «стартового» числа a₀^*_00000000 . Положить a₀^*  {3, 19, 259, 4099, 65539, 1048979, 2147483647}

Сравнить по точности датчики, реализующие МКМ при  = 65539 и  = 78125 (a₀^* = ).

Сравнить по точности МКМ-датчики при различных значениях  из заданного в пакете множества возможных значений. Положить a₀^* = .

4. Датчики Макларена-Марсальи (ММ-датчики) М₁ и М₂ используют в качестве простейших датчики D₁ и D₂, реализующие МКМ при следующих значениях параметров:

М₁ . D₁ :  = a₀^* = 65539,

D₂ :  = 65539, a₀^* = 256959681;

М₂ . D₁ :  = a₀^* = 1078318301,

D₂ :  = 1078318301, a₀^* = 860574881;

Сравнить по точности датчики М₁ и М₂.

Сравнить по точности и быстродействию ММ-датчик М₁ из задания 6 и МКМ-датчик с параметрами  = a₀^* = 65539.

5. Осуществить моделирование M = 100 реализаций СВ 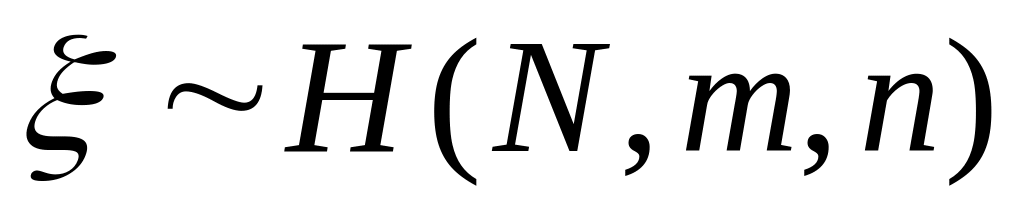. Исследовать точность моделирования с помощью тестов и графического анализа. Рассмотреть случаи: N = 100, m = 5, 10, 25, 50, n = 10, 20.

6. С помощью моделирования СВ с законами распределения 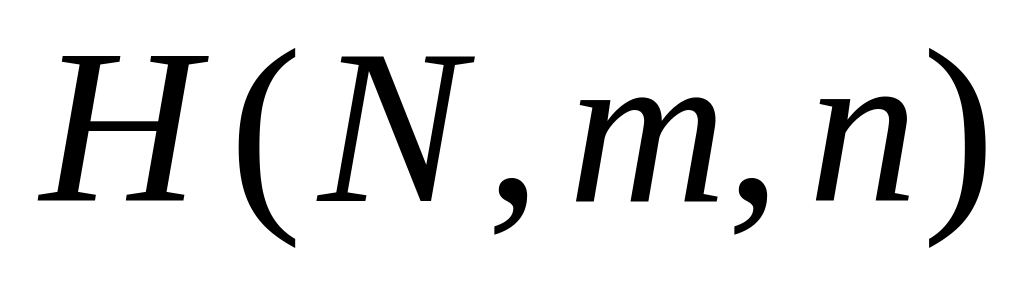, , 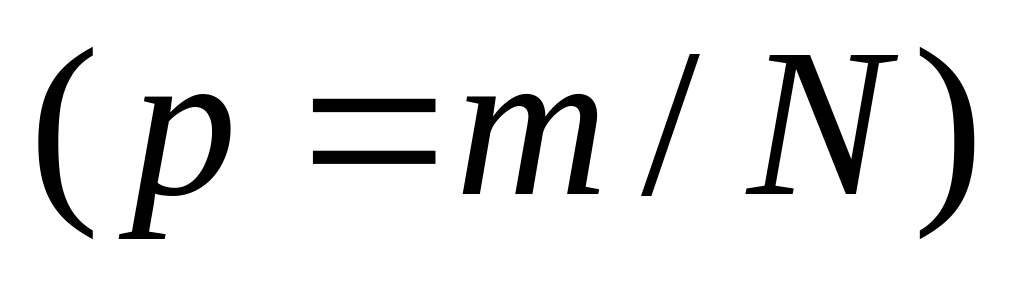, , 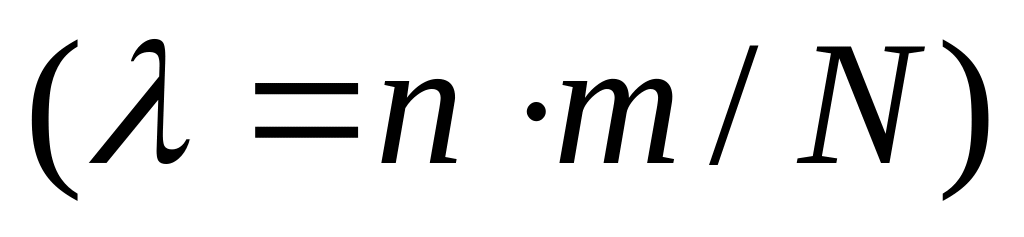исследовать возможность и точность аппроксимации гипергеометрического распределения другими законами: биномиальным (14.1), Пуассона (14.2), нормальным (14.3):

1. N = 1000, m = 100, 50, 25, 10, 5;

2. N = 1000, m =100, n = 10;

3. N = 1000, m =50, n = 20;

4. N = 2000, m = 100, n = 200;

5. N = 3000, m = 150, n = 300;

6. N = 4000, m = 200, n = 300.

Распределение Пуассона

7. Осуществить моделирование M = 100 реализаций СВ 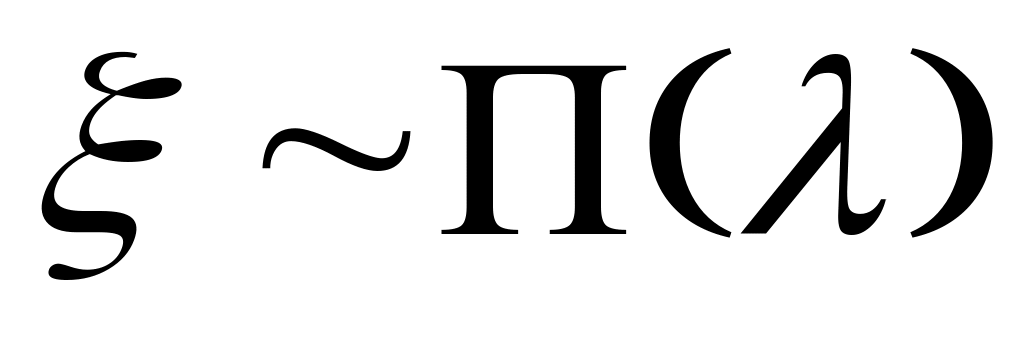. Исследовать точность моделирования с помощью тестов и графического анализа. Рассмотреть случаи: .

7. С помощью моделирования M = 100 реализаций СВ и СВ исследовать возможность и точность аппроксимации распределения Пуассона нормальным. Рассмотреть случаи: .

7. С помощью моделирования M = 100 реализаций СВ и СВ проиллюстрировать соотношение между распределениями:

.

Положить: .

7. Сравнить по точности и быстродействию методы моделирования СВ , реализованные в ППП СТАТМОД.