Лекции / Лекции поэлектротехнике(1-аячасть базового курса) / C00K22TO
.DOCЛЕКЦИЯ №22.
Несинусоидальные периодические токи.
Разложение несинусоидальной периодической функции в
периодический ряд.
На практике кривые эдс, токов и напряжений отличаются от идеальной синусоиды, оставаясь периодическими. Это связано с несинусоидальностью магнитной индукции в зазорах генераторов, наличием ряда нелинейных элементов в цепях и т.п. Поэтому результаты расчетов, полученные при идеализации формы напряжений и токов, оказываются верными только приближенно. Допустимость идеализации определяется как назначением цепи, так и степенью несинусоидальности. Особенно недопустима идеализация в линиях передачи информации, что связано с искажением или полной потерей передаваемой информации.
Для анализа цепей при несинусоидальных токах применяется разложение несинусоидальной функции в тригонометрический ряд Фурье. Возможность такого разложения основывается на том, что всякая периодическая функция, удовлетворяющая условиям Дирихле, т.е. имеющая на конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть представлена гармоническим рядом:
где
- постоянная
составляющая,
-
основная синусоида или первая гармоника,
-
высшие гармоники.
Раскрыв синусы суммы и приняв
,
,
получим:
,
где
,
,
.
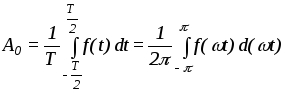При этом
,
.
Ряд может быть представлен и в комплексной форме записи:
,
где
,
- комплексные значения синусоидально
изменяющихся функций (гармоник).
Иногда для более простой записи вводят условно отрицательную частоту:
,
или в комплексной форме записи:
.
Если периодическая функция задана не аналитически, а в виде графика, то можно заменить интегралы суммами. Для этого период делят на «m» равных частей, каждая из которых
.
Тогда
,
,
,
где
- значение
функции при аргументе
,
,
-
значения этих функций при
.
Разложение упрощается, если исследуемая кривая обладает симметрией.
При симметрии относительно оси абсцисс:
.
Обладающая такой симметрией кривая приведена на рисунке.
Подстановка в
условие симметрии рядов
и
:
,
приводит к
.
Следовательно, в разложении кривых, симметричных относительно оси абсцисс, содержатся только нечетные гармоники. Ряд принимает вид:
.
При симметрии относительно оси ординат:
.
Обладающая такой симметрией кривая приведена на рисунке.
Подстановка в условие симметрии рядов показывает, что в этом случае ряд не содержит синусов, и разложение принимает следующий вид:
.
При симметрии
относительно начала координат
.
На рисунке изображена обладающая таким свойством кривая:
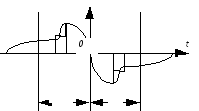
Аналогичным способом можно показать, что ряд в этом случае не содержит постоянной составляющей и косинусов:
.
В качестве примера рассмотрим разложение в ряд трапецеидальной кривой.
Ввиду симметрии относительно оси абсцисс и начала координат в разложении не будет постоянной составляющей, косинусоид и четных гармоник. Кроме того, ввиду симметрии достаточно рассмотреть четверть периода.
Амплитуды гармоник:
.
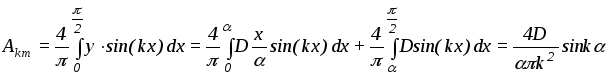Разложение принимает вид:
.
Приведем также разложения в ряд прямоугольной и треугольной кривых:
.
.
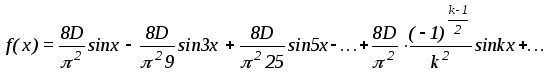В учебных пособиях по ТОЭ приводится большое число различных кривых и их разложение в ряд Фурье.
Совокупность
амплитуд
и фаз
называют спектром функции. Периодическая
функция обладает дискретным частотным
спектром.
Спектр
можно
характеризовать зависимостями амплитуд
и фаз
от частоты
.
Максимальные, средние и действующие значения
несинусоидальных токов.
Под максимальным
значением
понимают наибольшее значение функции
за период.
Среднее значение определяется как среднее по модулю:
.
В случае, если за весь период функция ни разу не меняет знака, среднее по модулю значение равно постоянной составляющей.
Обычно в расчетах пользуются действующим значением эдс, токов, и напряжений, которые определяются по формуле:
.
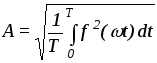Разложив заданную функцию в ряд и подставив в выражение для действующего значения, получим:
Заметим, что
возведение ряда в квадрат здесь возможно,
так как
ряд абсолютно
сходится при любом значении
.
Окончательно
.
Для токов, эдс и напряжений:
,
,
.
В электроэнергетике, где кривые преимущественно симметричны относительно оси абсцисс, для оценки несинусоидальности пользуются:
коэффициентом формы:
(для синусоиды
),
коэффициентом амплитуды:
(для синусоиды
),
коэффициентом искажения:
(для синусоиды
).
По стандарту напряжение промышленной сети считается практически синусоидальным, если действующее значение всех высших гармоник не превышает 5% действующего значения напряжения основной частоты. Коэффициент искажения такой кривой с точностью до долей процента равен единице.
В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник:
.
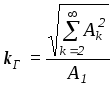При отсутствии постоянной составляющей:
.
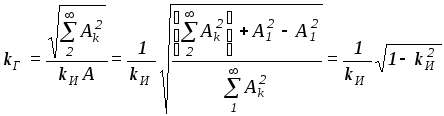(для синусоиды
).