Приклади розв’язування задач

Задача 1 Через блок, що має масу 80 г, перекинутий канат, до кінців якого підвішені тягарці з масами 100 г і 200 г. 3 яким прискоренням будуть рухатися тягарці, якщо їх залишити самі на себе? Тертям і масою каната знехтувати.

Дано: m = 80 г = 0,08 кг m1=100 г = 0,1 кг m2=200 г = 0,2 кг

а - ?

Розв’язок

Застосуємо для розв’язання задачі основні закони поступального і обертального руху. До кожного з тягарців, що рухаються, прикладені дві сили: сила тяжіння , яка направлена униз, і сила натягу каната , яка направлена вгору.

Оскільки прискорення тягарця масою m₁ направлене вгору, то:

1) Запишемо другий закон Ньютона для поступального руху тягарців m₁ і m₂ у векторному вигляді:

2) Спроектуємо цю систему рівнянь на вісь , як показано на рисунку,

врахувавши, що , що є наслідком нерозтяжності канату:

(1)

Згідно з основним законом динаміки обертального руху обертальний момент М, що прикладений до диска, дорівнює добутку момента інерції І диска на його кутове прискорення ε:

(2)

Визначимо обертальний момент. Сили натягу діють не тільки на тягарці, а й на диск. За третім законом Ньютона сили і , що прикладені до ободу диска, однакові за величиною силам і відповідно, але за напрямком їм протилежні: і . При русі тягарців диск обертається з кутовим прискоренням ε за годинниковою стрілкою, тому що 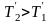. Обертальний момент, що прикладений до диска, дорівнює добутку різниці цих сил на плече, яке дорівнює радіусу диска r, тобто

Моменті інерції диска ; кутове прискорення зв’язане з лінійним прискоренням тягарців співвідношенням . Підставивши у формулу (2) вирази для М, І та ε, отримаємо:

,

звідки

(3)

Після підстановки (1) в (3) одержимо:

,

звідки

(4)

Підставимо числові значення: m = 0,08 кг; m₁ = 0,1 кг; m₂ = 0,2 кг.

Отримаємо:

.

Відповідь: a = 2,88 м/с².

Задача 2 Визначити прискорення тягарців а₁, а₂, а₃ і силу натягу ниток Т₁, Т₂, Т₃, зображених на малюнку. Вважати нитки нерозтяжними, тертям і масою ниток та блоків знехтувати.

m₁=4 кг Розв’язок.

m₂=2 кг Рівняння динаміки поступального руху для кожного з тягарців:

m₃=1 кг

а₁-?, а₂-?, а₃-?, Т₁-?, ; ;

Т₂-?, Т₃-?

Враховуючи те, що , а , знаходимо прискорення:

T₁

T₃

T₂

T₁

m₃g

m₂g

m₁g

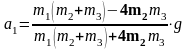= 2 м/с²

=4 м/с²

=16 Н; 32 Н.

Відповідь. а₁=2 м/с², а₂=а₃=4 м/с², Т₁=32 Н, Т₂= Т₃=16 Н.

Задача 3 На похилій площині, що утворює з горизонтом кут , знаходиться тіло масою = 2 кг (рис. ). Тіло рухається вгору по похилій площині під дією зв'язаного з ним невагомою і нерозтяжною ниткою, перекинутою через блок, вантажу масою = 20 кг. Початкові швидкості тіла і вантажу дорівнюють нулю, коефіцієнт тертя тіла = 0,1. Визначити прискорення, з яким рухаються тіла, і силу натягу нитки. Блок вважати невагомим, тертям знехтувати.

Розв'язання. На тіло , яке рухається по похилій площині, діє сила тяжіння , сила натягу нитки , сила тертя і сила реакції опори . На вантаж діє сила тяжіння і сила натягу нитки . Тут – прискорення вільного падіння. Другий закон Ньютона (рівняння руху) для цих тіл буде мати вигляд

, (12)

, (13)

де , - прискорення руху тіл.

Із умови невагомості і нерозтяжності нитки та відсутності тертя випливає, що , .

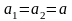Виберемо для тіла систему відліку хОу так, як показано на рисунку. Тоді рівняння руху цього тіла в проекціях на осі х і у запишеться так

, (14)

. (15)

Із співвідношення (15) знайдемо та підставимо у рівняння (14), врахувавши, що , тоді отримаємо

, (16)

де - коефіцієнт тертя.

Рівняння руху вантажу у проекції на вертикальну вісь має вигляд

. (17)

Розв'язавши систему рівнянь (16) та (17) відносно а, після простих перетворень отримаємо

(18)

Знаючи а, підставивши співвідношення (18) у вираз (17) знайдемо силу натягу нитки

.

Після підстановки числових значень фізичних величин отримаємо

м/c²,

=28,2 Н.

Перевіримо розмірності отриманих величин

,

.

Відповідь: 8,4 м/c², 28,2 Н.

Задача 4 Тіло масою m = кг знаходиться на екваторі. Визначити, як зміниться значення сили, що діє на поверхню Землі, якщо тіло, що рухається зі сходу на захід з постійною швидкістю = 20 м/с, змінить напрям свого руху на протилежний.

Розв’язання

Систему координат зв'яжемо з поверхнею Землі, де знаходиться тіло. У цьому випадку система рухається разом з Землею з прискоренням, тобто вона є неінерційною системою. На тіло діятиме сила інерції, що дорівнюватиме геометричній сумі сили, яка виникає при обертанні системи з кутовою швидкістю , і сили Коріоліса, оскільки тіло рухається вздовж екватора з певною швидкістю, тобто

У проекції на вісь ОХ, що проходить через центр Землі і точку, де знаходиться тіло в певний момент часу, результуюча сила, яка діятиме на тіло для першого випадку (рис. 4 , а) дорівнюватиме

де P- вага тіла, тобто сила, з якою тіло діятиме на Землю в певній точці; сила інерції; - сила Коріоліса.

Оскільки (тут -радіус Землі), то рівняння запишеться у вигляді

Запишемо рівняння для визначення результуючої сили для випадку, коли напрямок руху тіла по екватору змінився на протилежний. Оскільки напрямок сили Коріоліса зміниться на протилежний (рис. 4 , б), тоді результуюча сила дії тіла на Землю дорівнюватиме:

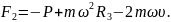
Згідно з умовою задачі необхідно знайти, як зміниться значення сили дії тіла на поверхню Землі. Знайдемо різницю між результуючими силами в першому і другому випадку, отримаємо