3.4. Теория полезности и ее основные элементы
Проблема рационального выбора является одной из основных экономических задач. ее постоянно решают все субъекты экономических отношений: производители пытаются выгодно вложить капитал в производство продукции, которая приносит доход; потребители стремятся приобрести товары с высокой потребительской ценностью по приемлемой цене; инвесторы пытаются сделать вложения, которые повысили стоимость капитала фирмы, и тому подобное. Каждая из этих задач решается в условиях риска и неопределенности. Принцип оптимальности принятия решений для этих задач нередко описывается функцией полезности.
Полезность - степень удовлетворения субъекта от потребления товара (получение услуги) или выполнение какого-либо действия.
В экономическом анализе полезность часто применяют для того, чтобы описать приоритеты в ранжировании наборов потребительских товаров и услуг (за предположение, что человек всегда делает рациональный выбор, то есть выбирает тот вариант, полезность которого, по ее мнению, максимальная). Понятие функции полезности позволяет сравнить потребительский эффект от покупки (продажи) различных, даже физически несовместимых, товаров. Полезность рассматривают как обобщенные определенным образом расходы или выигрыше, когда все ценности сведено к одной шкалы. Для измерения полезности можно использовать универсальную единицу «ютилях» (от англ. Utility - полезность) или приводить показатель в произвольных единиц (например, денежных).
Для определения полезности в условиях риска вводят общепринятое понятие лотереи, где эксперту предлагают сравнить две альтернативы:
1) значение показателя X;
2) лотерею - получить Хmin с вероятностью (1-р) или Xmax с вероятностью р. Величину вероятности р изменяют до тех пор, до¬кы, по мнению эксперта, значение показателя X и лотерея L (Хmin, г, Xmax) не станут эквивалентными ( XL (Хmin, г, Xmax)). Полезность худшего результата обычно оциню¬еться как 0 (U (Xmin) = 0), а лучшего - 1 или 100 (могут быть произвольные значения, но всегда U (Xmin) <U (Xmax)).
пример 1
Рассматривают два варианта инвестирования средств (20 тыс. Грн.):
1) приобретение государственных безрисковых облигаций с доходом 1000 грн. (Вероятность 1);
2) игра (лотерея): выигрыш 2100 грн. с вероятностью 0,5 и проигрыш 50 грн. (Накладные расходы на организацию) с вероятностью 0,5.
Необходимо дать рекомендации относительно направления инвестирования.
решение
1. Средний выигрыш:
- Приобретение государственных облигаций 1000 × 1 = 1000 грн .;
- Игра (лотерея) 2100 × 0,5-50 × 0,5 = 1025 грн.
Вывод: по отношению к среднему выигрышу рассмотрены альтернативы почти эквивалентны, и если игрок нейтральный к риску, он выберет второй вариант. Если он склонен ли подвержена риску, то выбор будет зависеть от финансового состояния игрока. Игроки с незначительным денежным доходом не будут рисковать, предпочтут гарантированном выигрыша. Для лиц с достаточным капиталом проигрыш 50 грн. незначительный, и они будут рисковать. Обязательно рисковать авантюристы (лица с патологической склонностью к риску).
Рациональное поведение исследовали американские экономисты Джон фон Нейман (1903-1957) и Оскар фон Моргенштерн (1902-1977) 1. Они вывели ее основные аксиомы.
Аксиома 1 (полноты). Когда предприниматель сталкивается с двумя любыми рядами событий, он всегда может определить, какая из них ему больше нравится, или ему все равно, какую последовательность событий выбрать: X> В (X больше нравится, чем в) X ≥ В (X больше нравится или безразлично X или В) X В (X и Y равноценны). Эта аксиома является основой классификации или сравнения последовательности событий, то есть дает возможность сравнивать все альтернативы.
Аксиома 2 (транзитивности). Преимущество различных низок событий последовательная, то есть, если X> В, В> Z, то X> Z. Это позволяет избежать фактора изменчивости вкусов субъекта (правильный выбор возможен только при наличии устойчивого вкуса).
Аксиома 3 (непрерывности). При соблюдении аксиомы транзитивности, если субъект с вероятностью 1 может получить альтернативу X, вероятностью p и (1-р) - соответственно альтернативы В и Z, существует такое г, при котором наборы X и Y + Z равноценны.
Аксиома 4 (независимости). Пусть существуют блага X и Y, которые, по оценке субъекта, одинаковые, и две лотереи, которые отличаются тем, что одна содержит X, а вторая - в, тогда эти две лотереи для субъекта одинаковы.
Аксиома 5 (неравных вероятностей). Если субъекту предложить две лотереи, которые дают одинаковый выигрыш с разной вероятностью, то он выбирает ту, вероятность выигрыша которой больше.
Аксиома 6 (составленной лотереи). Когда выигрышем одной лотереи является билет другой лотереи, то субъект принимает решение только по соображениям вероятности конечного выигрыша.
По Нейманом полезность варианта X определяется вероятностью р (Х), при которой лице безразлично, что выбирать: X - гарантировано, или лотерею L (Хmin, г, Xmax).
Пусть лотерея L обеспечивает выигрыш (события) Х1, Х2, ..., Xn с соответствующими вероятностями p1, р2, .... рn и полезностями U (X1), U (Х2) ... U (Xn). Средний выигрыш (математическое ожидание) и ожидаемую (среднюю, наиболее вероятной) полезность определяют соответственно по формулам:
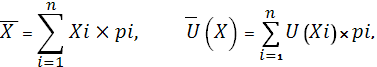
где X, U (Х) - средний выигрыш и ожидаемая (средняя) полезность выигрыша; Xi - и-и вариант выигрыша (события) р i - вероятность i-го варианта выигрыша; U (Хi) - полезность i-го варианта выигрыша.
Взаимосвязь риска с функциями полезности определяется понятием детерминированного эквивалента. Детерминированный эквивалент лотереи - это гарантированная сумма получения которой эквивалентно участия в лотерее и гарантирует лицу такую же полезность, как и участие в рискованном деле, есть
(3.1.)
Лицо, принимающее решение, называют неподверженным к риску, когда для нее наиболее приоритетной является возможность получить гарантированно ожидаемый выигрыш в лотерее, чем взять в ней участие.
По теории полезности можно сделать вывод, что полезность лотереи совпадает с математическим ожиданием полезности ее случайных результатов. В соответствии с этим условие несклонности риску приобретает следующий вид:
(3.2.)
то есть полезность ожидаемого дохода больше ожидаемой полезности. ОПР не подвержена риску тогда и только тогда, когда ее функция полезности вогнута.
Для
функции полезности можно рассчитать
премию за риск в лотерее (
(х)) как разницу между ожидаемым выигрышем
и детерминированным эквивалентом:
(3.3.)
По своему физическому смыслу премия за риск (надбавка за риск) - это сумма в единицах измерения показателя X, которой субъект управления согласен уступить из среднего выигрыша, чтобы избежать риска, связанного с лотереей, и получить гарантированный доход без риска.
Когда лицо, принимающее решение, наталкивается на лотерею, менее приоритетную, чем состояние, в котором она в данный момент находится, то возникает вопрос, сколько бы она заплатила (в единицах измерения критерия X) с своем неучастии в этой лотерее (избегание ее) .
Страховая сумма (CC) - это величина детерминированного эквивалента с противоположным знаком:
(3.4.)
Условие несклонности риску приобретает следующий вид:
(3.5.)
то есть полезность ожидаемого дохода меньше ожидаемой полезности. ОПР подвержена риску тогда и только тогда, когда ее функция полезности выпуклая, а график развернутый звоном вниз. Премия за риск в случае склонности к риску показывает, сколько средств инвестор может дополнительно получить или потерять, рискуя.
Условие равнодушия к риску приобретает следующий вид:
(3.6.)
ОПР безразлична к риску тогда и только тогда, когда ее функция полезности линейна, а график - прямая. Премия за риск в случае равнодушия к риску всегда равна нулю.
Рассмотрим примеры функций полезности:
Примеры различных функций полезности:
U (Х) = а + bХ- растущая (при b> 0) или ниспадающая (при b <0) функция полезности для субъекта, нейтрального к риску (рис. 3.7);
Рисунок 3.7. Растущая и убывающая функция полезности для субъекта, нейтрального к риску
U (Х) = 1оga (Х + b) - функция полезности для субъекта, склонных к риску, с уменьшающейся полезности (X> - b) (рис. 3.8);
Рисунок 3.9. Функция полезности для субъекта, склонного к риску с уменьшающейся полезности
U (X) = ecX - функция полезности для субъекта, постоянно неподверженного (при с> 0) или склонного (при с <0) к риску (рис. 3.10);
Рисунок 3.10. Функция полезности для субъекта, постоянно не подверженного или склонного к риску
U (Х) = сХ2- возрастающая функция полезности для субъекта, склонного (при c <0) или неподверженного (при с <0) к риску (рис. 3.11);
Рисунок 3.11. Функция полезности для субъекта с растущей склонностью или несклонностью к риску
U (Х) = а + bх + х2 (Х <b / с) - функция полезности для субъекта с возрастающей (при с <0) или уменьшающейся (при с> 0) склонностью к риску (рис. 3.12) ;
Рисунок 3.12. Функция полезности для субъекта с возрастающей или изменяемой склонностью к риску
U (X) = - функция с интервальной нейтральностью (склонностью - несклонностью) к риску (рис. 3.13).
Рисунок 3.13. Функция полезности с интервальной нейтральностью к риску
На рис. 3.13 можно выделить несколько зон склонности лица к риску: (0, 20) - нейтральность; (20; 40) - неподверженность; (40, 60) - склонность; (60; 80) - нейтральность; (80; 100) - неподверженность; (0, 50) - глобальная неподверженность.
В
теории рынка ценных бумаг широко
используется квадратичная
функция полезности вида:
(3.7.)
где А - заданное число.
Содержание этой функции такой инвестор считает полезным для себя увеличить значение эффективности, но желает избежать отклонения этой эффективности от ожидаемого значения. Чем больше А, тем сильнее тенденция предотвращения риска, то есть А - мера несхильнос¬ти к риску, а 1 / А - мера склонности к риску.
С помощью функции полезности можно рассчитывать вероятность банкротства:
,
если
Или
0, если
где K - начальный капитал.
Методика построения функции полезности для любого экономического показателя состоит из следующих шагов:
Шаг 1. Выявить лучшие и худшие из возможных допустимых показателей и присвоить им значения полезности соответственно 100 и 0 (если полезность оценивается по 100-балльной шкале).
Шаг 2. Рассмотреть несколько промежуточных показателей и указать их значение полезности (каждым экспертом отдельно).
Шаг 3. Рассчитать средние оценки полезности промежуточных значений, указанных экспертами.
Шаг 4. Если наблюдается рассеивание значений какого-либо из показателей, то нужно вернуться к шагу 2, чтобы согласовать мнения экспертов для достижения приемлемого диапазона рассеивания оценок (шаги 2-4 могут повторяться несколько раз).
Шаг 5. Определение функции полезности путем построения функции регрессии методом наименьших квадратов (проще функция полезности - уравнение прямой). Вид и аналитическая форма функции полезности свидетельствует об отношении субъекта, принимающего решение, к риску.
пример 2
Определение полезности с помощью математических функций.
Фирма может принять решение на основе трех показателей эффективности, применяя различное отношение к риску: неподверженность, склонность, нейтральность. Показатели эффективности задано лотереями: L1 = (20; 0,4; 10), L2 = (5; 0,5; 6), L3 = (10; 0,7; 30).
Неподверженность риску задана функцией полезности: U (x) =
= 1 - 2e- 0,1x.
Склонность задано функцией полезности: U (x) = 0,4х.
Нейтральность задано функцией полезности: U (x) = 4 + 1,2х.
Рассчитать премию за риск (надбавку) и определить, каким отношением к риску может воспользоваться фирма.