§1.8 Франк – Герц тәжірибелері

Д.Франк пен Г.Герцтің жасаған тәжірибесі Бор постулаттарының дұрыс екендігін дәлелдеді. Олар ішінде сынап буы бар разрядтық түтік алып, оның қыл сымын (F) қыздырғанда одан ұшып шыққан электрондар оң зарядталған торға қарай қозғалып тізбекте ток жүреді, бұл токтың күші F пен N арасындағы потенциалдар айырмасына, яғни үдетуші потенциалға байланысты(1.9-сурет).

1.9 Сурет

Бұл байланысты Франк пен Герц зерттеп тормен (N) пластинка (Р) арасындағы потенциалдар айырмасы шамамен 0,5В, энергиясы 0,5 электрон вольттан кем электрондар (N) тордан өтіп, Рколлекторға жете алмайды. Үдетуші потенциал (V) нөлден бастап ұлғайтылғанда ток күші алғаш термоэлектрон тог күші бағынатын заң бойынша өсіп V=4,9В болған кезде ол токкүші нөлге дейін кеміген, одан әрі V артқанда тогкүші тағы күшейіп, V=9,8 В болғанда ток кенет қайтадан кеміген(1.10-сурет).

Оны Франк пен Герц былай түсіндіреді. Электрондар сынап буының атомдарымен соғылады да, соқтығысу серпімді болса, онда электронның бағыты аздап өзгередіоның энергиясы өзгермейді. Себебі электронның массасы сынап буының атомының массасынан көп кіші, егер соқтығысу серпімсіз болса, онда электрон атомға өзінің кинетикалық энергиясын түгел береді, осыдан электронның энергиясы кемиді, атомның энергиясы артады – сынап атомы қозады. Егер электрон энергиясы 4,9эв-тен кем болса, оның сынап атомымен соқтығысуы серпімді болады да, электрон энергиясы кемімейді, оның қозғалыс бағыты өзгереді, бірақ ақырындап Р-пластинкаға жетеді. Үдетуші потенциал артқанда тог күші де артады. Үдетуші потенциал 4,9эв-болса, онда электронның соқтығысуы серпімсіз болады, оның кинетикалық энергиясы толығынан сынап буының атомына беріледі де электрон N-сеткаға бөгеліп қалып, Р-пластинкаға жете алмайды, ток күші нөлге дейін кемиді. Нәтижесінде сынап атомының энергиясы көбейеді де ол қозады. Үдетуші потенциал 9,8В болғанда бір электрон сынап буының екі атомын, 14,7В болғанда – үш атомын қоздырады. Олай болса үдетуші потенциал 4,9 В болғанда, түтіктегі сынап буы жарық шығарады, онда толқын ұзындығы 0,2537 мкм спектр сызығы байқалады.

1.10-сурет

Олай болса сынап буының атомы, электронмен соқтығысқанда 4,9эв энергияны толық жұтады. Атомның энергиясы кез келген шама болмайды, тек белгілі шамаға тең болады.

Бордың жиіліктер шарты бойынша атомның шығаратын жарық толқынының жиілігі

Егер сынап буының атомы электроннан 4,9эв энергия алып, жарық шығарады, яғни қозады.

§1.9 Сутегі атомының эллипстік орбитасы

Эллипстік орбитамен қозғалған электрон энергиясы үлкен жарты остің және кванттық санның мөлшерімен анықталмай, басқа жаңа кванттық сан (l) арқылы анықталсын. Онда орбитада орналасқан электрон энергиясына қандай жаңа әсерлесулер болатынын қарастырсақ, онда осы орбитада қозғалған электрон өте үлкен жылдамдықпен қозғалады, оның массасы жылдамдыққа байланысты өзгереді. Ал дөңгелектік орбитадағы электрон жылдамдығы тұрақты, олай болса орбитаның әр бөлігінде электронның массасы өзгермей тұрақты болып қалады. Егерде электрон эллипстік орбитада қозғалса, орбитаның әр бөлігінде, жылдамдығы әртүрлі, яғни атом ядросына жақын келгенде жылдамдығы үлкен, ал ядродан алыстаса жылдамдығы баяулайды. Олай болса, эллипстік орбитада қозғалған электронның массасы да өзгереді. Сонда электрон жылжымайтын эллипстік осте ғана қозғалып қоймайды, өз жазықтығында айналатын эллипстеде (1.11-сурет) айналады.

1.11-сурет

Бұл айналмалы қозғалыс үлкен болу үшін, эллипстік орбитаның үлкен жарты осі созылыңқы болуы керек және қатынасы неғұрлым кіші болған сайын, электрон массасының өзгеруі арта түседі.

Олай болса, орбитадағы электрон энергиясын анықтағанда орбита мөлшерін ғана есепке алып қоймай оның формасында еске алып, орбита формасын анықтайтын шаманы да табу керек. 1.12-сурет бойынша электронның импульс моментін табамыз.

1.12-сурет

Бірінші күйдегі дөңгелек орбитадағы импульс моменті

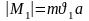(1.9.1)

Екінші күйдегі,яғни эллипстік орбитадағы импульс моменті.

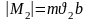(1.9.2)

Бірінші орбитадағы электронның толық энергиясы:

(1.9.3)

Екінші орбитадағы электронның толық энергиясы:

(1.9.4)

егер ; болса, онда (1.9.1) және (1.9.2) формуладағы импульс моментін тұрақты мәндер бойынша өрнектейік:

(1.9.5)

бұдан

(1.9.6)

ал

(1.9.7)

(1.9.6) формуланы (1.9.7) – формулаға қойсақ, онда

(1.9.8)

Бұдан эллипстық орбитада қозғалған электронның элементар импульс моменті -ге еселеніп квантталған болады.

(1.9.8) теңдіктегі шамаға тең - бұл орбиталдық кванттық сан, ол эллипстық траекториямен қозғалған электронның импульс моментін сипаттайды. Яғни мәндерге ие болып, эллипстық орбита формасын сипаттайды. Мұндағы болса, электрон қозғалысы, атом ядросынан өтетін түзуге сәйкес келеді.

Классикалық механика бойынша мұндай қозғалыс болуы мүмкін емес. Ал кванттық механикада бөлшектер қозғалысы толқындық процесс, олай болса мұндай процесске рұқсат етіледі.

Сонымен эллипстық орбита екі кванттық санмен сипатталады, оның біреуі n – бас кванттық сан, екіншісі орбитаның үлкен жарты осі - а. Олар қозғалмайтын эллипстік орбитадағы электрон энергиясын сипаттайды, ал -кванттық саны эллипстық жарты остерінің қатынастарын және өз жазықтығында қозғалған эллипстік орбита бойындағы электрон энергиясын анықтайды.

Мұндай жағдайлар электронды ядроға тартатын Кулондық күштен басқа күштер әсер етпесе энергиясы өзгермейді. Егер қандай да бір қосымша күш пайда болса, онда орбитаның үлкен жарты осі (а) өзгермейді, ал кіші жарты осі (в) өзгеріп, электрон әртүрлі энергияға ие болады. Бұл жағдайда толық энергия бас кванттық санмен (n) , үлкен жарты остің өлшемдерінен басқа да параметрлерге, яғни - қосымша кванттық санғада (l) байланысты болады.

§1.10 Бор – Зоммерфельд кванттау ережелері