Пример:

К цепи переменного тока с активным сопротивлением R= 8 Ом приложено напряжение u = 45 sin( t+30°). Определить активную мощность цепи и уравнение мгновенного значения тока.

Решение:

1. Действующее значение напряжения

2. Действующий ток в цепи I= .

3. Мощность цепи P = U∙I = 32∙4 = 128 Вт.

4. Уравнение мгновенного значения тока i = 5,64 sin ( t+30°).

4.2.2. Цепь с индуктивностью

Рис. 4.2.3. а)

Если к указанной катушке приложить синусоидальное напряжение, то в цепи будет протекать синусоидальный ток, переменный магнитный поток которого индуцирует в катушке ЭДС самоиндукции:

где - скорость изменения тока;

=

Напишем для цепи, изображенной на рис. 4.2.3. уравнение второго закона Кирхгофа.

Так как, R цепи равно нулю, то iR=0, поэтому u+ =0, откуда и u= - т.е. равна и противоположна по направлению напряжению на зажимах цепи. Подставив значение в эту формулу получим:

Из этой формулы видно, что напряжение на зажимах цепи опережает по фазе ток на угол 90° или ток отстает по фазе от напряжения на угол 90°. Амплитуда напряжения , откуда .

Разделив обе части последней формулы на , получим выражение для действующего значения тока = ; I= .

Выведенная формула есть выражение закона Ома для данной цепи, следовательно, L представляет величину сопротивления этой цепи, называемого индуктивным сопротивлением и обозначаемого

= =

Рис. 4.2.3. б)

Из формулы следует, что индуктивное сопротивление цепи пропорционально индуктивности L и угловой частоте переменного тока.

Индуктивным сопротивлением называется величина, характеризующая противодействие ЭДС самоиндукции переменному току.

Выразим значения напряжения, тока и индуктивного сопротивления в комплексной форме.

; .

Комплекс индуктивного сопротивления найдется так:

= = = .

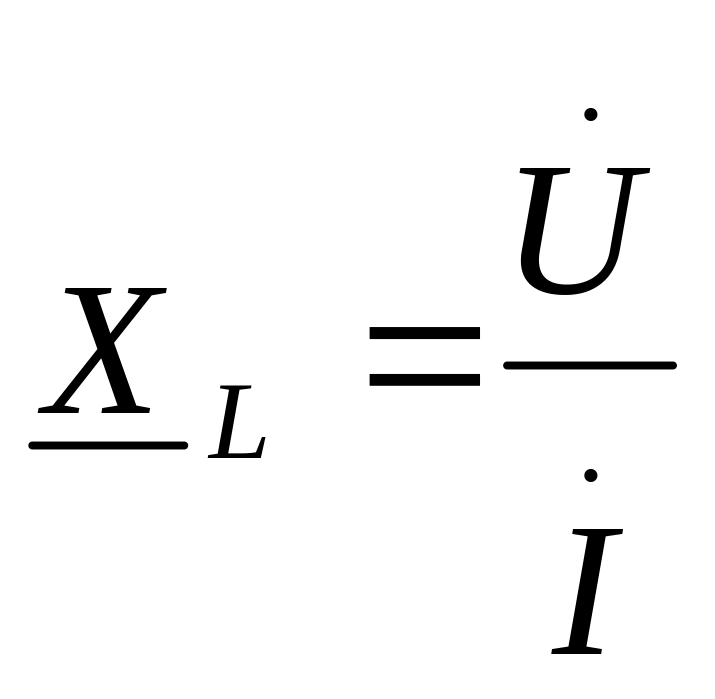В алгебраической форме комплекс выразится так:

= ,

Поскольку cos =0; sin =1.

Временная и векторная диаграммы индуктивной цепи

На рис. 4.2.3. в) изображена векторная диаграмма, из которой видно, что в цепи с «чистой» индуктивностью напряжение U опережает по фазе ток на 90°, а ЭДС самоиндукции отстает по фазе от тока на 90°.

На рис. 4.2.3.г) изображен график мощности.

Рис. 4.2.3.г

Мощность цепи

;

Отсюда видно, что кривая мощности имеет синусоидальную форму и частоту, в 2 раза большую, чем частота тока, напряжения.

4.2.3. Цепь с индуктивностью и активным сопротивлением.

На практике используются реальные катушки индуктивности, которые обладают активным и индуктивным сопротивлением.

На схеме рис. 4.2.3.1 индуктивность и активное сопротивление отделены друг от друга и показан как участки цепи для удобства расчетов.

Рисунок 4.2.3.1

Допустим, что в цепи протекает синусоидальный ток

Напряжение цепи распределится на двух участках

Приведем векторную диаграмму цепи (рис.4.2.3.2 )

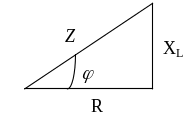
Треугольник напряжений Треугольник сопротивлений

Рисунок 4.2.3.2

Из теоремы Пифагора:

Действующее значение тока определим по закону Ома:

При расчете цепи используются формулы:

1. Из треугольника напряжений

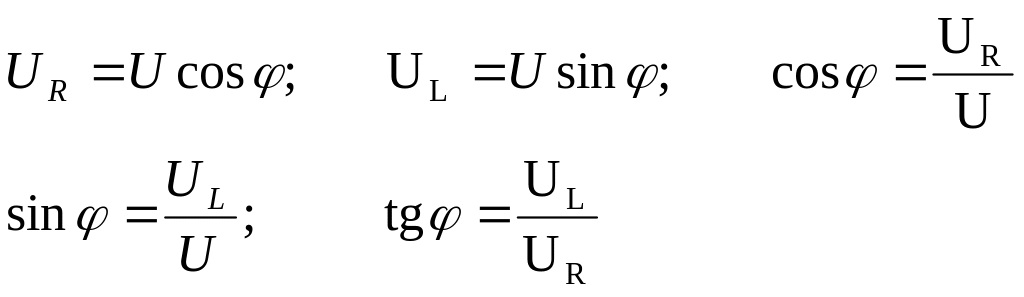
2. Из треугольника сопротивлений

Если умножим стороны треугольника напряжений на ток, то получим треугольник мощности

где, - активная мощность цепи

- реактивная мощность

- полная мощность

или

- называется коэффициентом мощности.

Он показывает, какую часть от полной мощности составляет активная мощность и характеризует энергию, которая безвозвратно преобразуется в другие виды энергии.

В символическом виде:

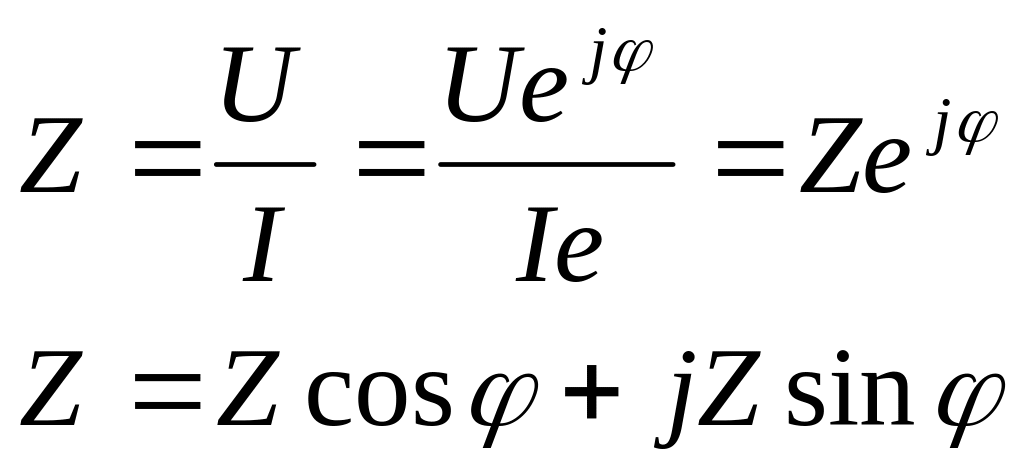
Из треугольника сопротивлений

поэтому Z в алгебраической форме

Пример:

Дано:

R= 30 Ом

L= 0.127 Гн

U= 120 В

f= 50 Гц

Опр: XL,Z,I,S

Написать уравнение мгновенных значений тока и напряжения.

Решение

1. Индуктивное сопротивление катушки

2. Полное сопротивление в комплексной форме

3. Ток в цепи

4. Амплитудное значение тока и напряжения

5. Напишем уравнение мгновенных значений тока и напряжения:

6. Комплекс мощности

ВА.

Вопросы для самоконтроля

1. Приведите свойства цепи с активным сопротивлением.

2. Свойства цепи с индуктивностью.

3. Запишите формулу полного сопротивления в символическом виде для цепи RL.

4. Запишите закон Ома для цепи с RL в комплексном виде.