
- •2)Задача про шлях точки у прямолінійному русі.
- •Означення визначеного інтеграла. Геометричний і фізичний зміст визначеного інтеграла.
- •Основні властивості визначеного інтеграла.
- •Формула Ньютона-Лейбніца
- •Обчислення визначеного інтеграла. Інтегрування підстановкою (заміни змінної).
- •Теорема. Якщо:
- •Обчислення визначеного інтеграла. Інтегрування частинами.
- •Інтегрування парних і непарних функцій в симетричних межах.
- •В першому інтегралі зробимо підстановку . Тоді
- •Наближене обчислення визначених інтегралів
- •Метод прямокутників
- •М етод трапецій
- •Метод парабол (формула Сімпсона)
Формула Ньютона-Лейбніца
Нехай
функція
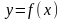 інтегрована на відрізку
інтегрована на відрізку
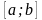 .
.
Теорема
.Якщо
функція
неперервна на відрізку
і
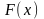 — яка-небудь її первісна, то має місце
формула
— яка-небудь її первісна, то має місце
формула
 .
.
Отриману рівність називають формулою Ньютона-Лейбніца.
Якщо
ввести позначення
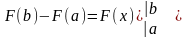 ,
то формулу Ньютона-Лейбніца можна
переписати так:
,
то формулу Ньютона-Лейбніца можна
переписати так:
 .
.
Формула
Ньютона–Лейбница дає зручний спосіб
обчислення визначе-ного інтеграла. Щоб
обчислити визначений інтеграл від
неперервної функції
 на відрізку
,
треба знайти її первісну функцію
і узяти різницю
на відрізку
,
треба знайти її первісну функцію
і узяти різницю
 значень цієї первісної на кінцях відрізка
.
значень цієї первісної на кінцях відрізка
.
Приклади.
 .
. ,
де
,
де
 при
при
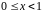 і
і
 при
при
 .
.
Тут
функція
має розрив у точці
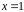 ,
але на кожному з проміжків
,
але на кожному з проміжків
 і
і
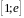 вона неперервна. Скористаємося з
адитивності інтеграла:
вона неперервна. Скористаємося з
адитивності інтеграла:

3)

 .
.
4)
○ .
.
Обчислення визначеного інтеграла. Інтегрування підстановкою (заміни змінної).
Нехай
для обчислення інтеграла
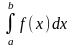 від неперервної функції зроблена
підстановка
від неперервної функції зроблена
підстановка
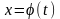 .
.
Теорема. Якщо:
Функція і її похідна
 неперервні при
неперервні при
 ;
;Множиною значень функції при є відрізок ;
 і
і
 ,
,
то
 .
.
Доведення:
Нехай
є первісною для
на відрізку
.
Тоді по формулі Ньютона-Лейбніца
.
Оскільки
 ,
то
,
то
 є первісною для функції
є первісною для функції
 .
Тому по формулі Ньютона-Лейбніца маємо
.
Тому по формулі Ньютона-Лейбніца маємо
 ■
■
Формула називається формулою заміни змінної в визначеному інтегралі.
Відзначимо, що:
при обчисленні визначеного інтеграла методом підстановки повертатися до старої змінної не потрібно;
часто замість підстановки застосовують підстановку
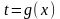 ;
;не слід забувати міняти межі інтегрування при заміні змінних!
Приклад.
Обчислити
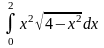 .
.
○ Покладемо
 ,
тоді
,
тоді
 .
.
Якщо
 ,
то
,
то
 ;
якщо
;
якщо
 ,
то
,
то
 .
.
Тому

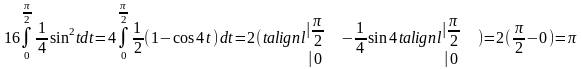 .●
.●
Обчислення визначеного інтеграла. Інтегрування частинами.
Теорема
.
Якщо
функції
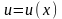 і
і
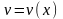 мають неперервні похідні на відрізку
,
то має місце формула
мають неперервні похідні на відрізку
,
то має місце формула
 .
.
Доведення:
На
відрізку
має місце рівність .
Отже, функція
.
Отже, функція
 є первісною для неперервної функції
є первісною для неперервної функції
 .
Тоді по формулі Ньютона-Лейбніца маємо:
.
Тоді по формулі Ньютона-Лейбніца маємо:
 .
Отже,
.
Отже,
 .■
.■
Формула називається формулою інтегрування по частинах для визначеного інтеграла.
Приклад.
Обчислити
 .
.
Розв’язання:
Покладемо
 .
Використовуючи формулу інтегрування
по частинах,
отримаємо
.
Використовуючи формулу інтегрування
по частинах,
отримаємо

Приклад.
Обчислити інтеграл
 .
○
.
○
Розв’язання:
Інтегруємо по частинах. Покладемо
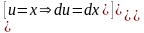 .
Тому
.
Тому
 .
●
.
●
Інтегрування парних і непарних функцій в симетричних межах.
Нехай
функція
неперервна на відрізку
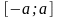 ,
симетричному відносно точки
.
Доведемо, що
,
симетричному відносно точки
.
Доведемо, що
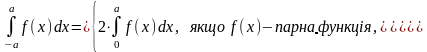
Розіб'ємо
відрізок інтегрування
на частини
 і
і
 .
Тоді за властивістю адитивності
.
Тоді за властивістю адитивності .
.
В першому інтегралі зробимо підстановку . Тоді

(згідно з властивістю: «визначений інтеграл не залежить від позначення змінної інтегрування»). Повертаючись до рівності (2), отримаємо
 .
.
Якщо
парна
(( ),
то
),
то
 ;
якщо функція непарна ((
;
якщо функція непарна ((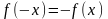 ),
то
),
то
 .
.
Завдяки доведеній формулі можна, наприклад, відразу, не проводячи обчислень, сказати, що
 ,
,
 .
.
