12)Единицы длины принятые в судовождении.
Для измерения расстояний в море, глубин, высот береговых ориентиров, а также скоростей судна, ветра и течения в судовождении применяются следующие единицы длины.
Морская миля — единица длины, равная длине одной минуте дуги меридиана земного эллипсоида. 1 миля = 1852,23 м
Кабельтов— единица длины, равная 0,1 мили, т. е. 185,2 м. В кабельтовых измеряют небольшие расстояния на море: • расстояния между судами при оценке безопасности плавания; • дальности, измеренные радиолокационными станциями.
Глубины морей и океанов, высоты гор и других ориентиров над уровнем моря выражаются в метрах. При пользовании английскими картами и другими пособиями по судовождению можно встретить другие единицы длины: сажень морская — единица длины, равная 1,83 м. Применяется для обозначения глубин на английских картах; фут — единица длины, равная 30,48 см. Применяется для измерения высот предметов на берегу и малых глубин.
13)Единицы скорости принятые в судовождении.
Основной единицей скорости, принятой в судовождении, является узел. Один узел соответствует скорости, при которой судно проходит за один час одну морскую милю: 1 уз = 1 миля/ч. В судовождении в узлах выражают скорости судов и морских течений. При решении некоторых задач скорость судов удобно выражать в кабельтовых в минуту (каб/мин). Скорость судна в кабельтовых в минуту используется для расчета пройденных расстояний за малые промежутки времени, измеряемые минутами. Скорость ветра, скорость звука в воде и ряд других скоростей в судовождении выражают в метрах в секунду (м/с).
14)Видимый горизонт наблюдателя
Глаз наблюдателя находится на некоторой высоте е над поверхностью Земли. Предположим, что глаз наблюдателя расположен в точке А,тогда расстояние МА= е. Лучи зрения из точки А расходятся по направлениям: АC1, АС2, АС3, АС4 и т. д. , касательным к поверхности земного шара. Геометрическое место точек касания луча зрения с земной поверхностью образует малый круг C1, С2, Сз, С4, который называется видимым горизонтом наблюдателя.
15)Дальность видимости горизонта.
С увеличением высоты наблюдателя плотность земной атмосферы понижается, и луч, преломляясь в ее различных по плотности слоях, распространяется не прямолинейно, а по некоторой кривой, в связи с чем наблюдатель видит горизонт не по направлению АС4 а по направлению АК, которое является касательной к криволинейному лучу АВ4 в точке наблюдателя. Следовательно, видимый горизонт будет представлен уже другой окружностью: В1, В2, В3, В4. Дальность видимого горизонта Д (в милях), равная дуге АВ4, определяется по формуле Д=2.08√е, где е—высота глаза наблюдателя в метрах.
16)Дальность видимости предмета.
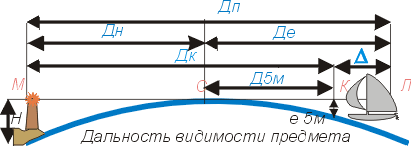
Предмет, который видит наблюдатель, также имеет определенную высоту Н . Поэтому дальность видимости предмета Д, будет равна расстоянию ЛМ, которое слагается из дальности видимого горизонта наблюдателя Де и дальности видимого горизонта предмета Дп. Формула Дп=2.08√е+√Н
17)Оптическая дальность видимости навигационных огней.
В навигационных пособиях и на морских картах дальность видимости маячных огней Дк рассчитана для высоты наблюдения 5 м и равна расстоянию МК. Дальность видимого горизонта с высоты глаза наблюдателя 5 м равна 4,7 мили. Если высота глаза наблюдателя больше или меньше 5 м, то к дальности видимости предмета Дк. указанной в пособиях, следует прибавить поправку d на действительную высоту глаза наблюдателя которая представляет собой разность расстояния межд;
дальностью видимого горизонта с высоты е и 5 м. ∆=2.08√е-2.08√5. Эта поправка будет иметь знак плюс, когда е>5 м, и знак минус, когда e<5M.
Дальность видимости маячного огня будет выражаться формулой:
Дп = Дк + d
где Дк — дальность видимого горизонта предмета (с карты);
d — поправка расстояния на высоту глаза наблюдателя.
Чтобы каждый раз не производить математических расчетов, в мореходных таблицах (один из видов навигационных пособий) даются дальности видимого горизонта для различной высоты глаза.
20)Система счёта направлений в море.
Для определения направления в плоскости истинного горизонта используются 4 системы деления горизонта: круговая, полукруговая, четвертная и румбовая. За основную взята круговая.
21)Круговая система счёта направлений.
В круговой системе весь горизонт делится на 360°. Счет направления ведется от 0 до 360° по ходу часовой стрелки от северной части истинного меридиана наблюдателя
22)Полукруговая система счёта направлений.
В полукруговой системе счет направлений ведется как от северной, так и от южной части меридиана наблюдателя в сторону Ost и W в пределах от 0 до 180°. Для направлений в полукруговом счете кроме величины угла обязательно указывается, от какой части истинного горизонта (N или S) и в какую сторону (к Оst или к W) отсчитано данное направление, например: N20°0Ost, S48°W, S54°Ost, N1б5°W. Чтобы перейти от направлений в полукруговом счете к направлениям в круговом счете, следует: — при направлениях от N к Оst отбросить буквы наименования, оставив сам угол без изменений; например, угол в полукруговом счете N125° Ost равен углу 125° в круговом счете; — при направлениях от N к W отбросить буквы наименования и взять численное дополнение заданного угла до 360°; например, направлению N140°W соответствует направление в круговом счете 220°; — при направлениях от S к Ost отбросить наименование и взять дополнение данного угла до 180°; — при направлениях от S к W отбросить наименование и к направлению в полукруговом счете, прибавить 180°. Пусть, например, требуется перевести в круговой счет следующие направления: N270 Ost, S132° Ost, S63°W, N98°W. В круговом счете эти направления соответственно будут: 27°, 48°, 243°, 262°.
23)Четвертная система счёта.
В четвертной системе каждая четверть горизонта делится на 90° и отсчет направлений ведется от северной или от южной части меридиана наблюдателя в сторону Ost или W в пределах от 0 до 90°. В этой системе направление показывается наименованием четверти (NОst, SOst, SW, NW) и соответствующим углом, например: NOst30°, NW64°, SOst73°, SW55°. Переход от четвертной системы к круговой осуществляется с соблюдением тех же правил, что и изложенные выше для перехода от полукруговой к круговой системе.
24)Румбовая система счёта.
На парусном флоте применяли румбовый счёт. По нему весь горизонт делился на 32румба (направления). В каждом из румбов – 11,25º. Четыре из них – север (N), юг (S), запад (W), восток (Е), называютсяглавными; четыре – северо-восток (NE), юго-восток (SE), юго-запад (SW), северо-запад (NW), называются четвертными. Восемь румбов, расположенных между главными и четвертными (например,NNE, ENE, ESE и т.д.) носят название трёхбуквенных румбов. Остальные шестнадцатьрумбов относятся к промежуточным.
Названия промежуточных румбов формируются чуточку сложнее.
Сначала идёт название ближайшего главного или четвертного румба, затем приставка „тэн“ , или иногда говорят „тэнь“ (ten – означает предлог «к» и обозначается в написании строчной буквой t), потом название главного румба, в сторону которого уклонён данный промежуточный румб. Например, NtW – норд-тэн-вест.
Наилучшим образом такая система понятна на приведённом рисунке.
