Тема 4. Афчх и лачх

4.1 Афчх разомкнутых и замкнутых систем

Рассмотрим замкнутую одноконтурную систему, структурная схема которой приведена на рисунке 4.1.

Рисунок 4.1 – Структурная схема замкнутой системы

ПФ разомкнутой системы равна произведению ПФ последовательно соединенных звеньев

(4.1)

Для простоты рассуждений рассмотрим частный случай, когда к₁ = к₂ = к и Т₁ = Т₂ = Т. Тогда выражение (5.1) примет вид

(4.2)

Для построения частотных характеристик системы необходимо в формулу (4.2) вместо оператора р поставить jω (р = jω). Комплексная переменная в знаменателе ПФ не допускается, поэтому числитель и знаменатель умножается на комплексно-сопряженное число.

(4.3)

В данном случае комплексная величина ПФ представлена в алгебраическом виде, т.е. состоящая из действительной и мнимой части W_p (jω) = X(ω) + jY(ω). В показательном виде комплексная переменная примет вид W_p (jω) = A(ω) e^jφ , где А(ω) – амплитуда ПФ; φ – угол между действительной осью комплексной плоскости и вектором ПФ.

Тогда формулу (4.3) можно представить и показательной форме

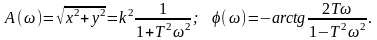(4.4)

Для построения АФЧХ необходимо изменять частоту от 0 до ∞ в любом из выражений ПФ разомкнутой системы (4.3) или (4.4).

В начале построения кривой АФЧХ находят две крайние точки при ω = 0 и ω = ∞. Тогда, пользуясь формулой (4.3), получим

при ω = 0 х (ω) = к²; у(ω) = 0 – точка лежит на действительной оси комплексной плоскости;

при ω = ∞ х (ω) = 0; у(ω) = 0.

Если использовать показательную форму (4.4), то при ω = 0 А (ω) = к²; φ(ω) = 0 – точка лежит на действительной оси комплексной плоскости;

при ω = ∞ А (ω) = 0; φ(ω) = 0.

Теперь необходимо определить точки пересечения кривой АФЧХ только с мнимой осью У комплексной плоскости, т.к. координатную функцию х (ω) при пересечении с действительной осью уже определили при ω = 0. Для этого приравняем действительную часть х (ω) к нулю и найдем частоту ω₀, а затем подставим ее в мнимую часть у(ω) формулы (4.3).

х (ω) = 0; 1 – Т² ω² = 0.

Тогда ω₀ = 1/Т – частота, при которой действительная часть х (ω) = 0.

Подставив полученную частоту в мнимую часть формулы (4.3), получим значение координаты точки пересечения кривой АФЧХ с мнимой осью у(ω₀) = - 0,5. Через тир точки можно приблизительно показать кривую АФЧХ. Более точную кривую строят при частотах от ω= 0 до ω₀ с произвольным шагом.

Рисунок 4.2 – АФЧХ разомкнутой системы

ПФ замкнутой системы (см. рисунок 5.1) равна

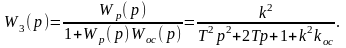(4.5)

Для построения АФЧХ используется не все выражение (4.5), а только знаменатель, называемый характеристическим уравнением замкнутой системы. Вид кривой характеристического уравнения лежит в основе частотного критерия Михайлова, а сама кривая АФЧХ называется кривой Михайлова.

Характеристическое уравнение замкнутой системы равно

Т²р² + 2Тр + 1 + к² к_ос = 0. (4.6)

Подставим р = jω в характеристический полином, получим

-Т²ω² + j 2Tω + 1+ k² k_oc = X(ω) + jY(ω) = (1+ k² k_oc - Т²ω²) + j 2Tω, (4.7)

где X(ω) = 1+ k² k_oc - Т²ω² – действительная часть вектора полинома;

jY(ω) = 2Tω – мнимая часть вектора полинома.

Кривая АФЧХ строится аналогично: изменяя частоту ω от 0 до ∞ находят точки координат на комплексной плоскости, подставляя дискретные значения частот в выражение (4.7). Степень полинома характеристического уравнения определяет квадрант окончания АФЧХ, т.е. вектора знаменателя ПФ при ω = ∞.

Находим координаты при двух крайних частотах:

при ω = 0 Х(0) = 1+ k² k_oc ; У(0) = 0;

при ω = ∞ Х(∞) = - ∞; У(∞) = ∞.

Частота ω₀, при которой происходит пересечение кривой с мнимой осью находится при Х(ω) = 0

1+ k² k_oc - Т²ω² = 0,

Подставив найденную частоту ω₀ в мнимую часть У(ω), получим значение координаты точки пересечения кривой АФЧХ с мнимой осью комплексной плоскости

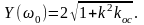
Рисунок 4.3 – АФЧХ замкнутой системы