9.2 Алгебраический критерий устойчивости

Рассмотрим способ применения критерия Гурвица для исследования корней характеристического уравнения.

. (9.6)

Критерий Гурвица позволяет оценивать расположение корней характеристического уравнения многочлена относительно мнимой оси переменной р. Для определения же устойчивости в z-изображении требуется определить расположение корней относительно окружности единичного радиуса (рисунок 9.3).

Рисунок 9.3 - Отображение границы устойчивости на W-плоскости

Следовательно, необходимо сделать преобразование окружности таким образом, чтобы единичная окружность превратилась бы в мнимую ось, а внутренность единичного круга отобразилась на левую полуплоскость Re<0. Такое отображение выполняется билинейным преобразованием

. (9.7)

Заменив переменную в (9.6), получим

, (9.8)

где D(w) – многочлен степени n от новой переменной w, причем

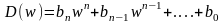. (9.9)

Для того, чтобы корни многочлена D(w) имели отрицательные вещественные части необходимо и достаточно, чтобы все определители Гурвица были положительными.

Рассмотрим для примера систему второго порядка n=2. Характеристическое уравнение для n=2 с учетом (9.9)

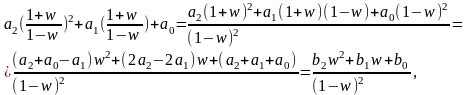
где ; ; .

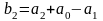Для систем второго порядка определители Гурвица будут положительными, если коэффициенты многочлена D(w) будут положительны, т.е. . Система будет устойчива, если

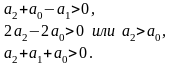(9.10)

Условия (9.10) для систем 2-го порядка называются критерием Шура-Кона.

Пример 1. Определить критическое значение периода квантования Т_кр, при котором система будет находиться на границе устойчивости.

Рисунок 9.4 – Структурная схема импульсной системы

Определим переходную функцию непрерывной части системы

Затем с помощью таблицы 10.2 определим ее z-изображение

Разомкнутая ПФ импульсной системы равна

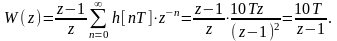
Знаменатель ПФ замкнутой импульсной системы является характеристическим уравнением, которое имеет вид

или z –1+10T=0.

Система будет на границе устойчивости, если

│z │= 1-10T = 1.

Отсюда T_кр = 0,2с.

Пример 2. Рассмотрим устойчивость замкнутой системы с фиксатором нулевого порядка, структурная схема которой приведена на рисунке 10.5.

Рисунок 9.5 – Структурная схема системы

ПФ замкнутой системы равна

.

Определим ПФ звена в прямой цепи в z-изображении

где d = е^(-Т/Т₁⁾.

Характеристическое уравнение системы равно

(9.11)

Поскольку характеристическое уравнение (9.11) 1-го порядка, то система будет устойчива, если для числителя 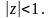Определим значение К, при котором система будет находиться на границе устойчивости при различных периодах квантования Т.

В этом случае

Полагая 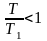и разлагая в ряд , а также ограничившись первыми 2-мя членами ряда, получим

Условие выполняется, если

Отсюда получаем, что при (T/T₁) = 0,1 К_кр = 19.

При (T/T₁) = 0,2 К_кр = 9.

Таким образом, в отличие от непрерывной системы цифровая система 1-го порядка может быть неустойчивой. Устойчивость системы зависит от периода квантования Т.