
- •Типовой расчет по теме: «дифференциальное исчисление»
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
Вариант №9
1. Найти область определения функции
![]() .
.
2. Построить область определения функции
![]() .
.
3. Найти пределы функций, не используя правило Лопиталя.
а)
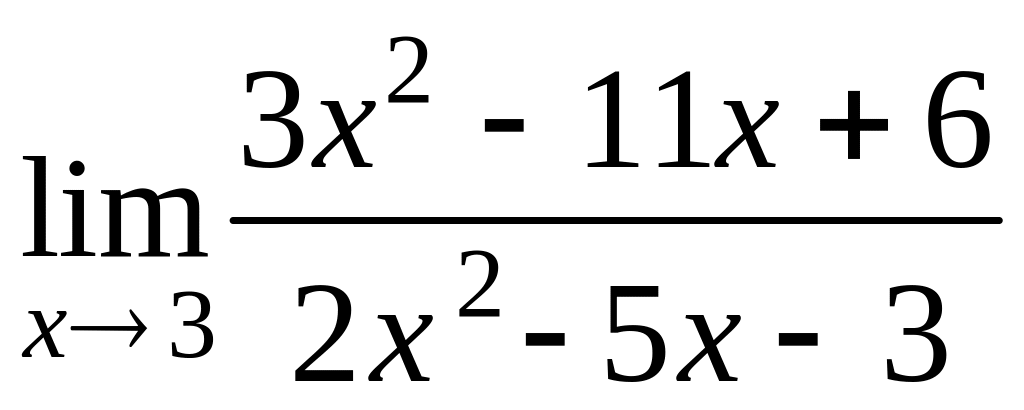 ; в)
; в)
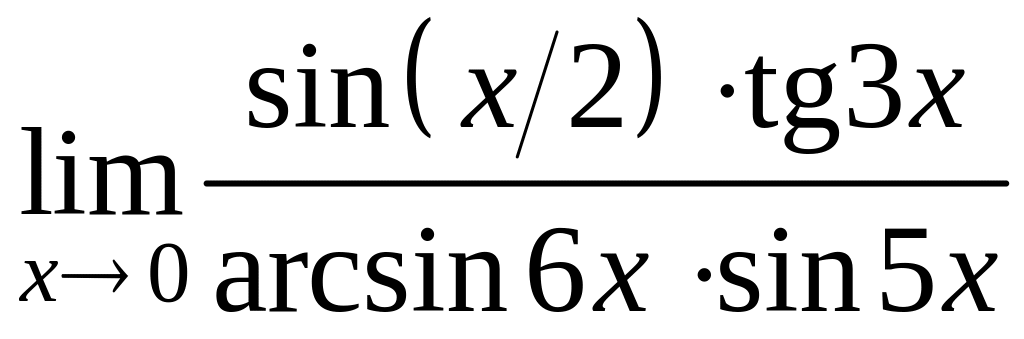 ;
;
б)
![]() ; г)
; г)
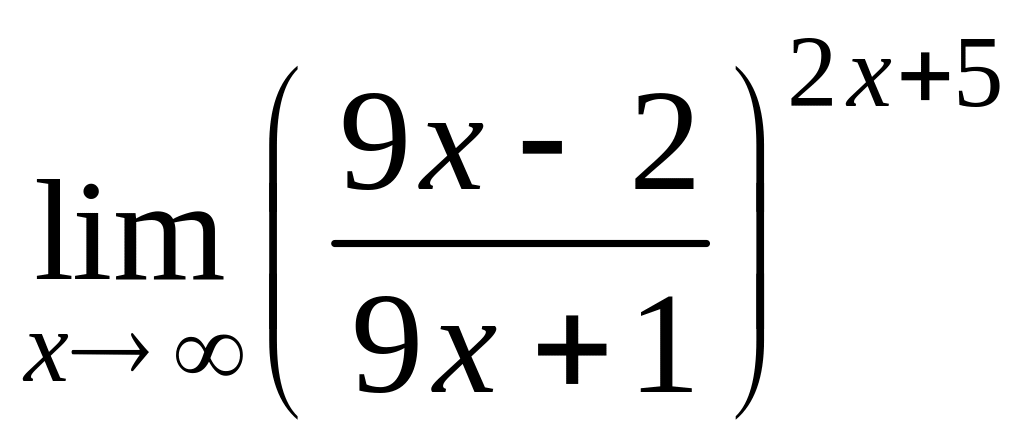 .
.
4. Исследовать функцию
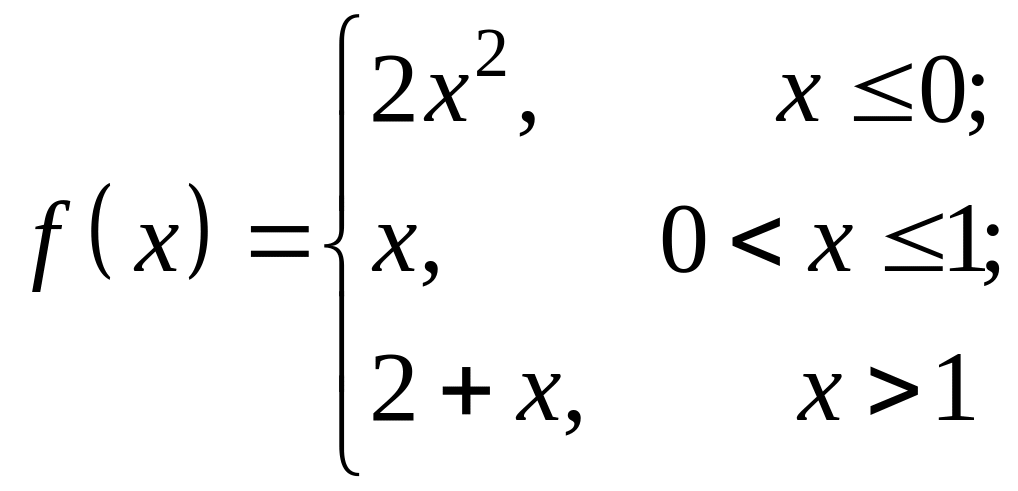 на непрерывность и определить характер
точек разрыва.
на непрерывность и определить характер
точек разрыва.
5. Найти производные функций и для одной из них найти дифференциал.
а)
![]() в)
в)
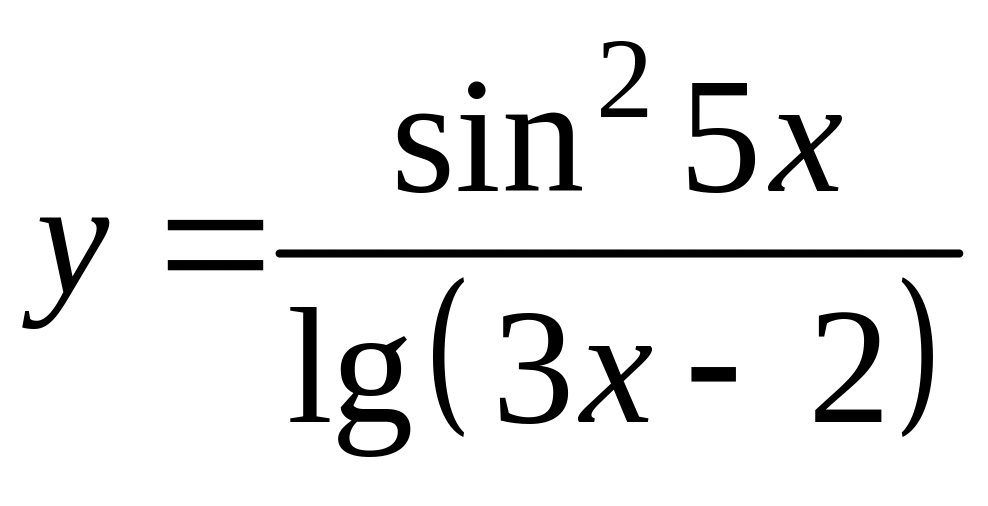
б)
![]() г)
г)
![]()
6. Найти и :
а)
![]() ; б)
; б)
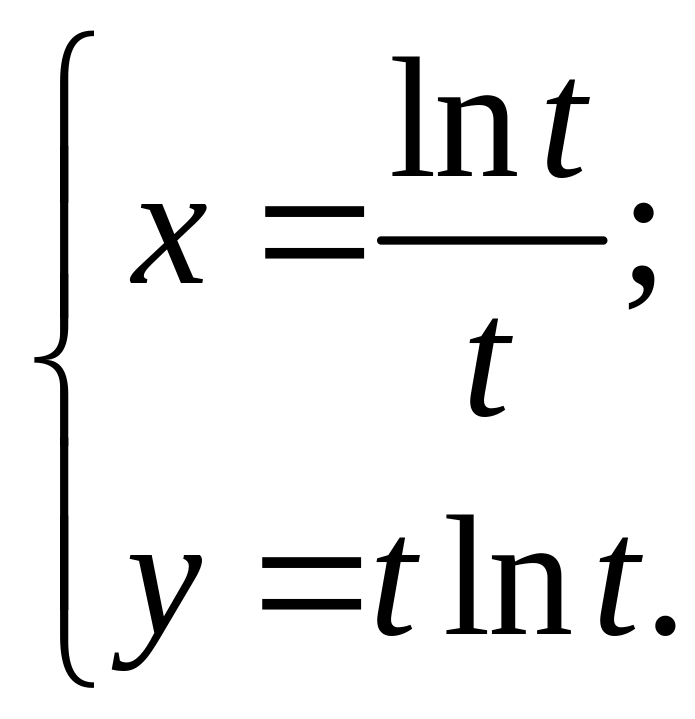
7. Записать уравнения касательной и
нормали к кривой
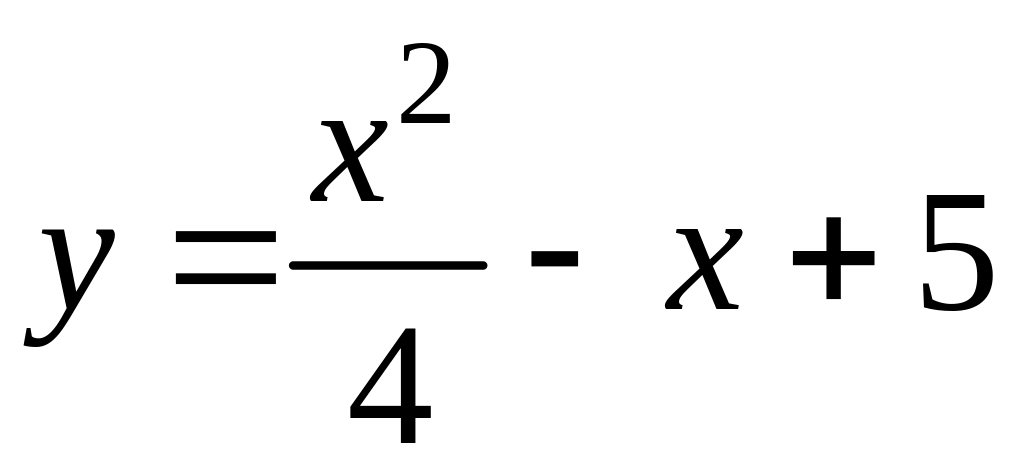 в точке с абсциссой
в точке с абсциссой
![]() .
.
8. Вычислить с помощью дифференциала
приближенное значение функции
![]() при
при
![]() .
.
9. Используя правило Лопиталя, вычислить
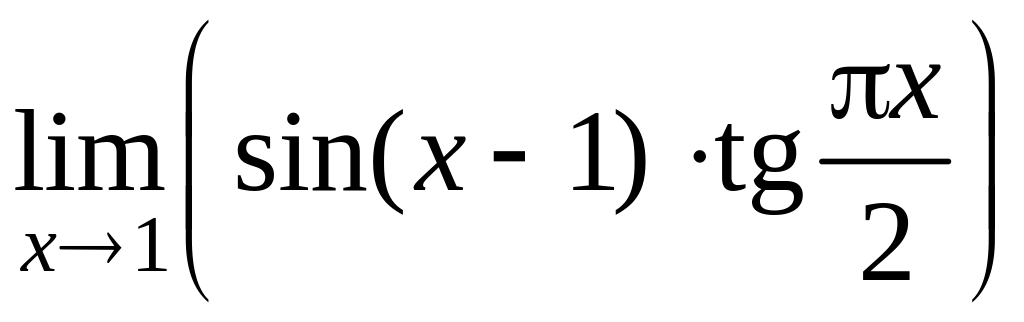 .
.
10. Найти частные производные первого порядка следующих функций:
а)
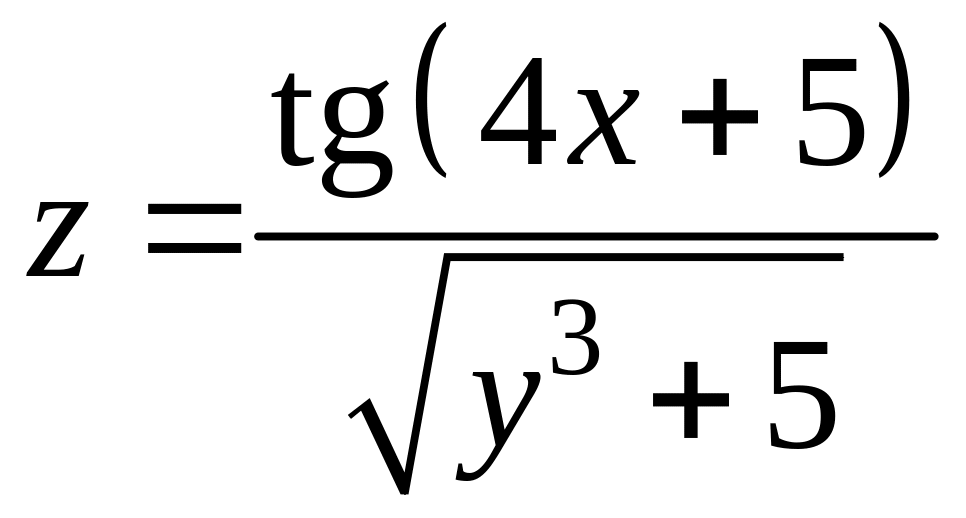 ; б)
; б)
![]() ; в)
; в)
![]() .
.
11. Найти дифференциалы первого и второго
порядка функции
![]() .
.
12. Провести исследование функции
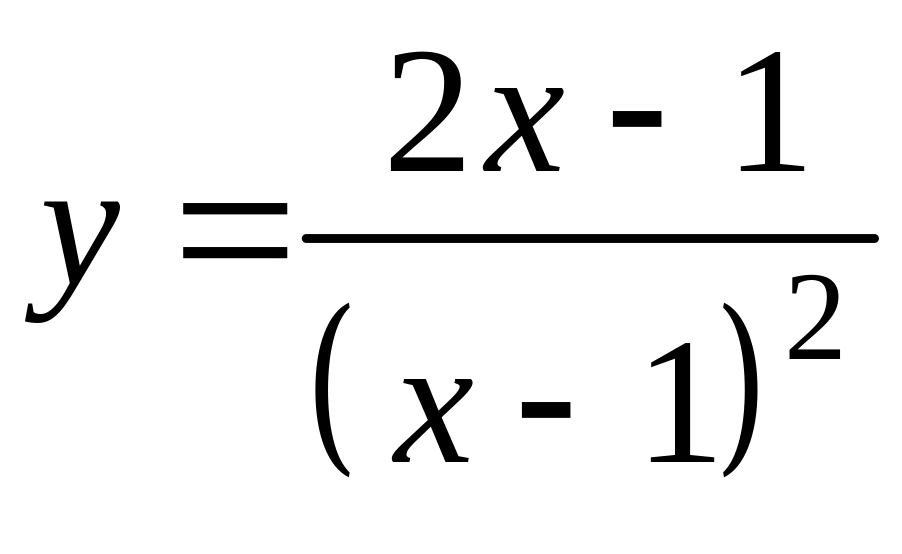 и построить ее график.
и построить ее график.
Вариант №10
1. Найти область определения функции
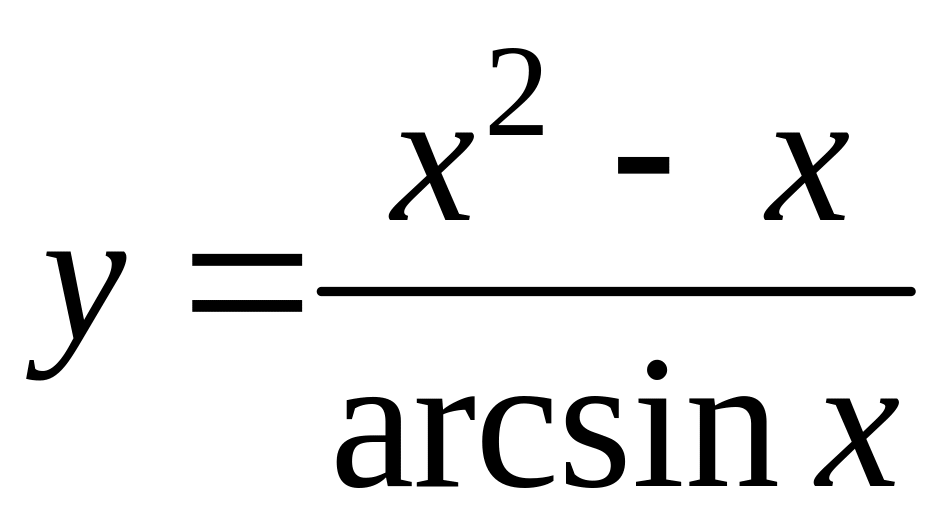 .
.
2. Построить область определения функции
![]() .
.
3. Найти пределы функций, не используя правило Лопиталя.
а)
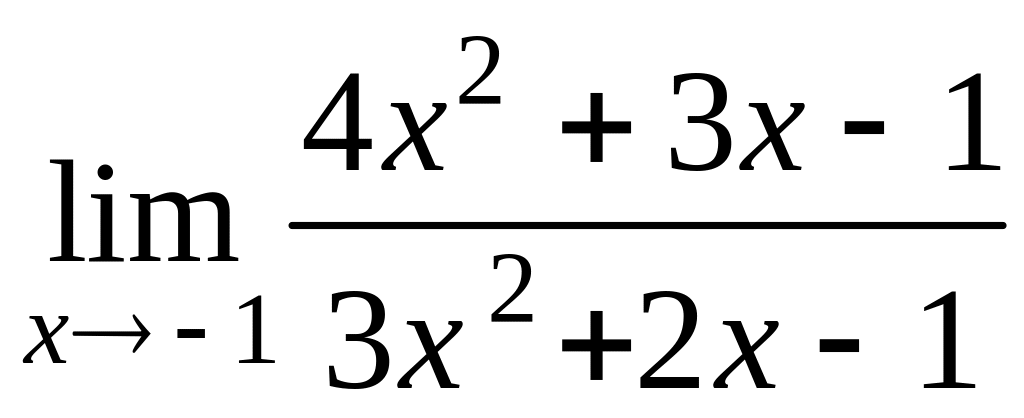 ; в)
; в)
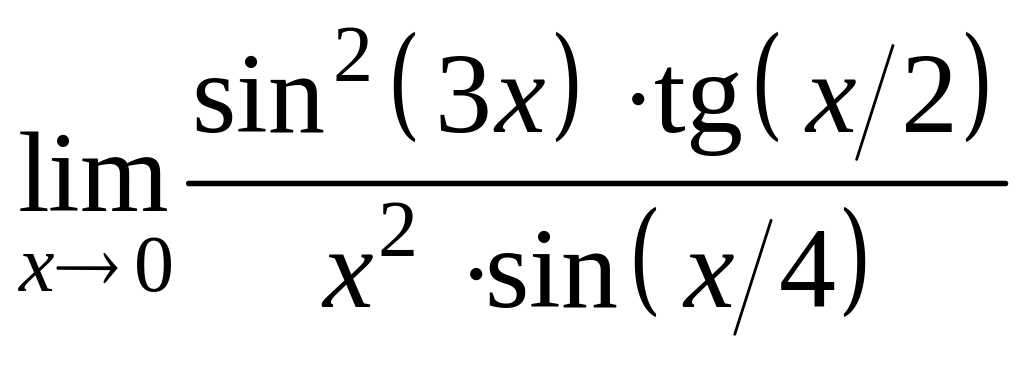 ;
;
б)
![]() ; г)
; г)
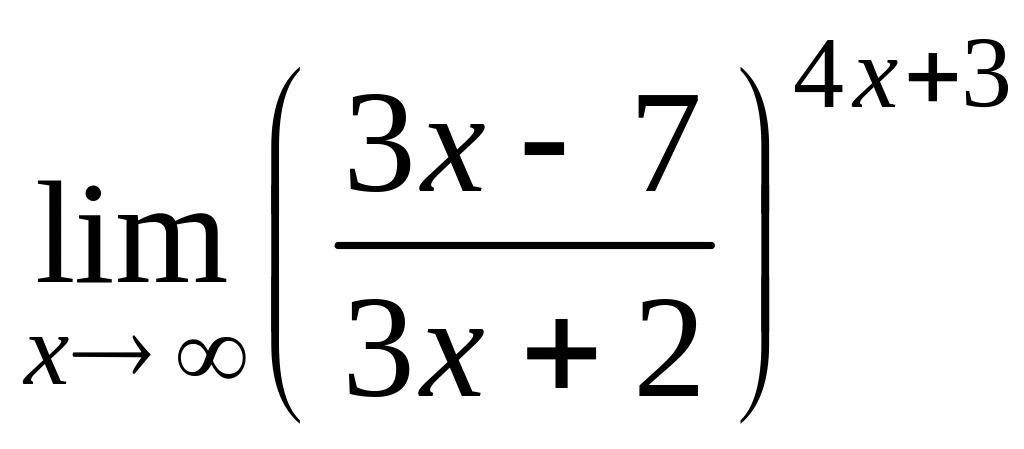 .
.
4. Исследовать функцию
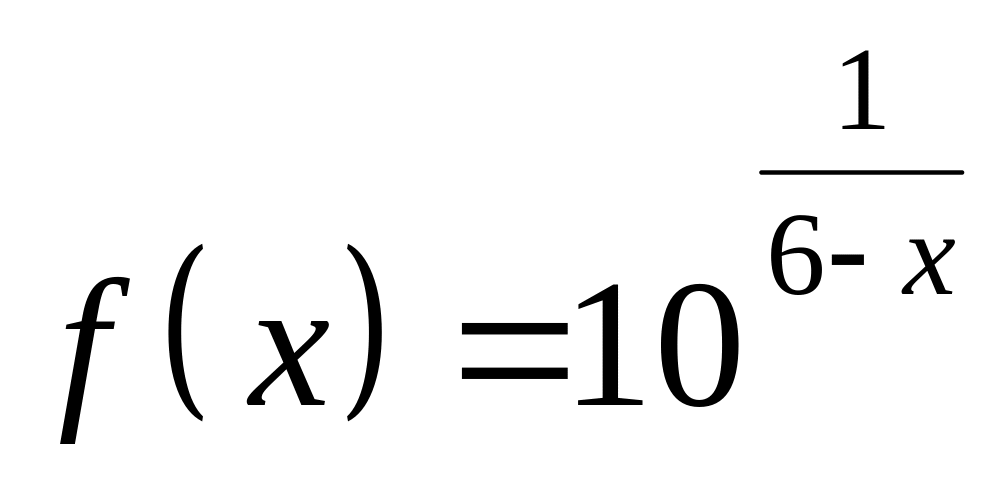 на непрерывность в точках
на непрерывность в точках
![]() .
.
5. Найти производные функций и для одной из них найти дифференциал.
а)
![]() в)
в)
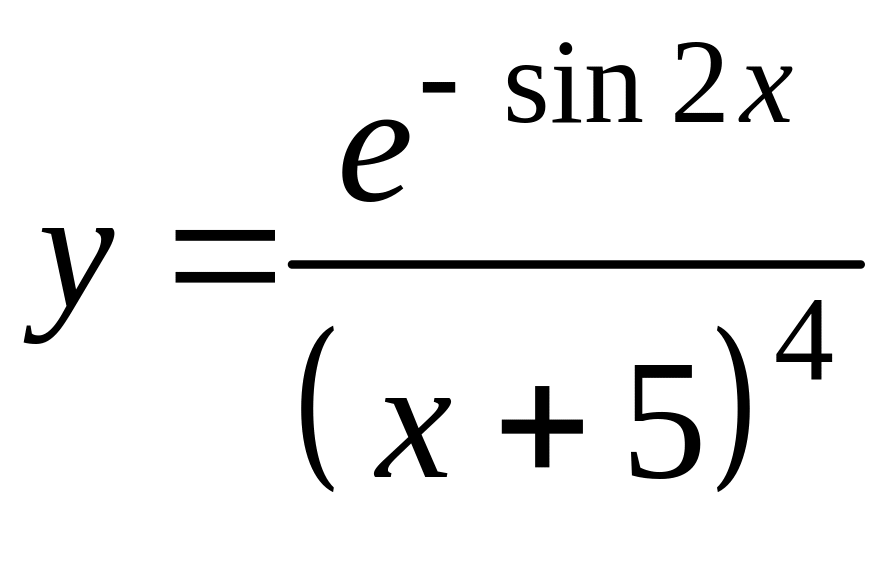
б)
![]() г)
г)
![]()
6. Найти и :
а)
![]() ; б)
; б)
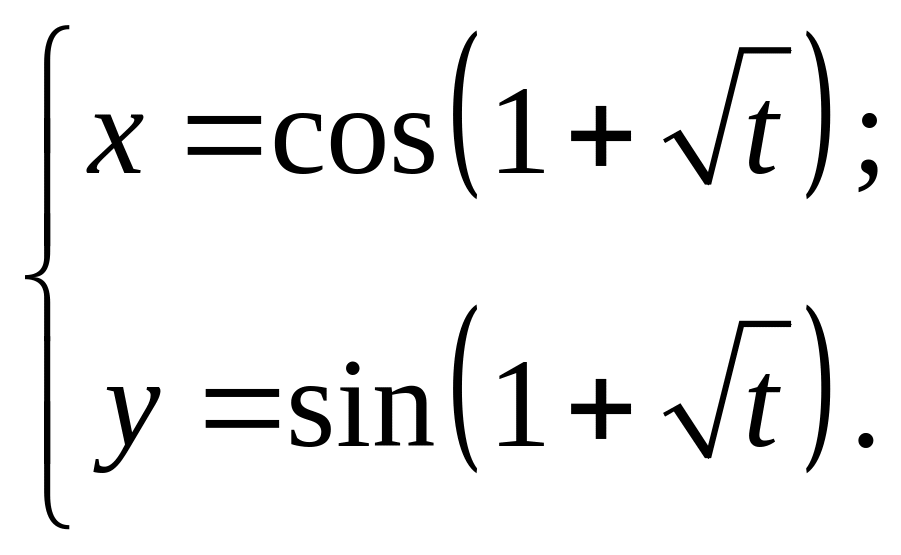
7. Записать уравнения касательной и
нормали к кривой
![]() в
точке А(2,1).
в
точке А(2,1).
8. Вычислить с помощью дифференциала
приближенное значение функции
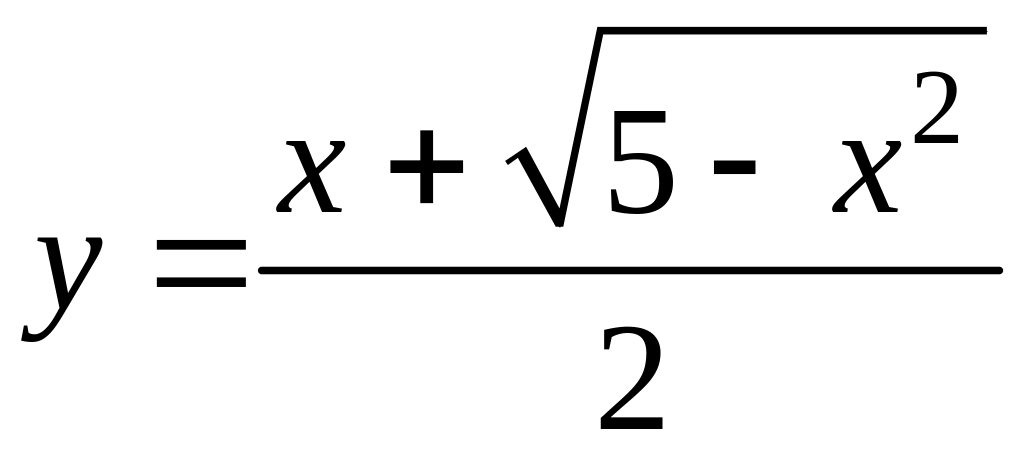 при
при
![]() .
.
9. Используя правило Лопиталя, вычислить
![]() .
.
10. Найти частные производные первого порядка следующих функций:
а)
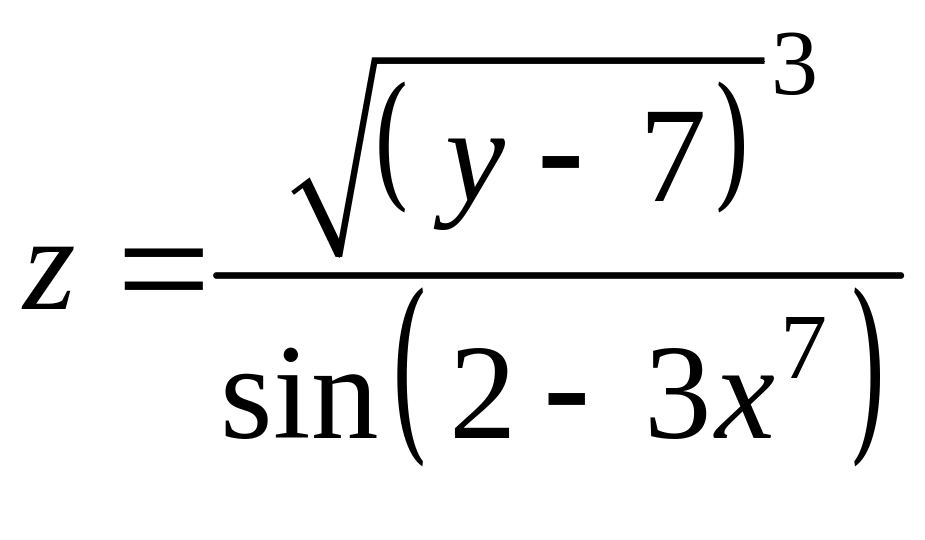 ; б)
; б)
![]() ; в)
; в)
![]() .
.
11. Найти дифференциалы первого и второго
порядка функции
![]() .
.
12. Провести исследование функции
![]() и построить ее график.
и построить ее график.
Вариант №11
1. Найти область определения функции
![]() .
.
2. Построить область определения функции
![]() .
.
3. Найти пределы функций, не используя правило Лопиталя.
а)
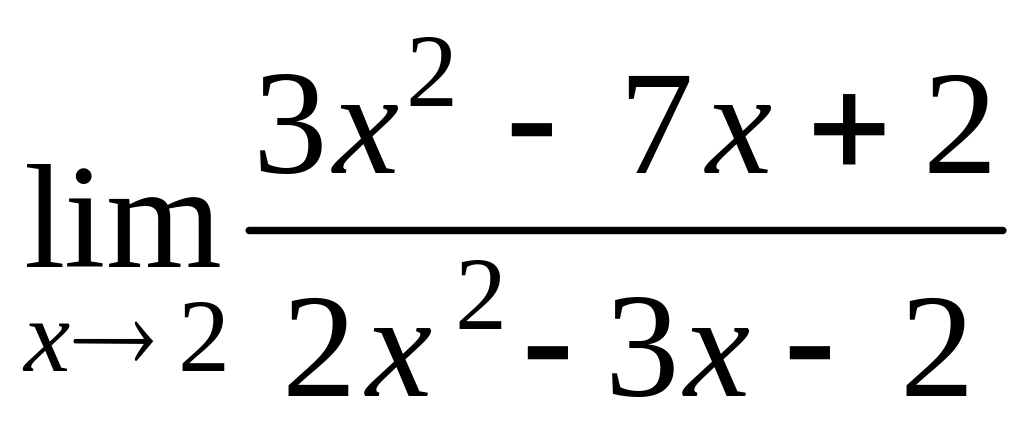 ; в)
; в)
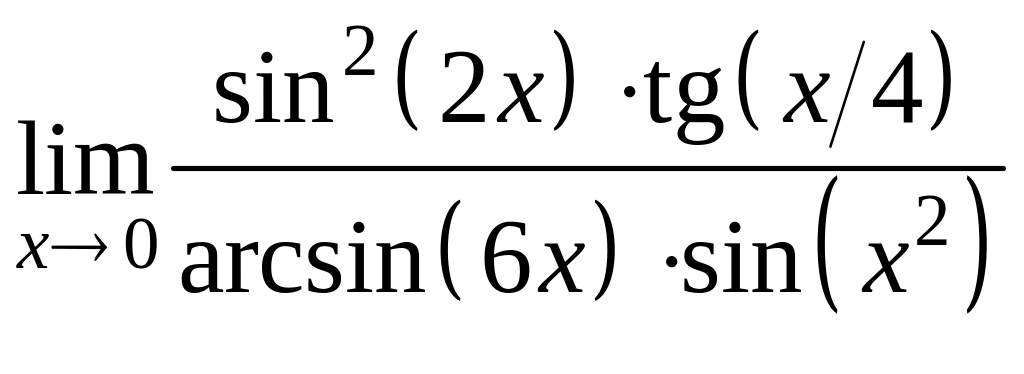 ;
;
б)
![]() ; г)
; г)
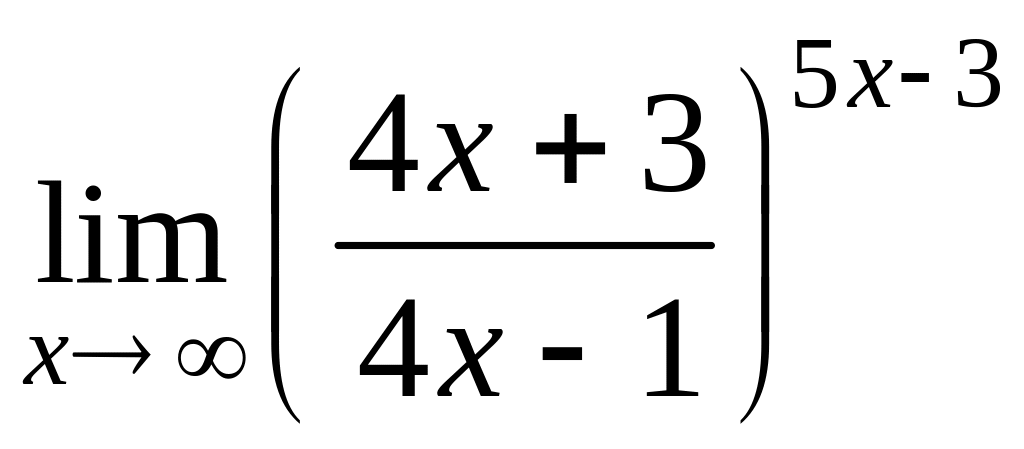 .
.
4. Исследовать функцию
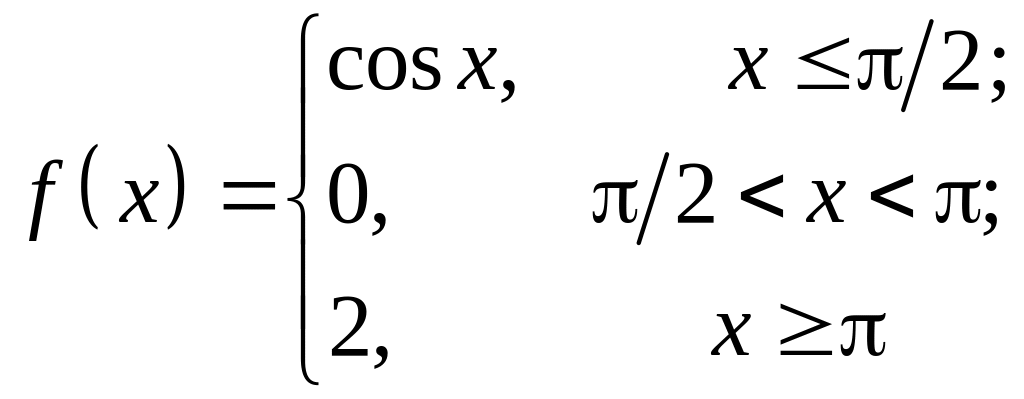 на непрерывность и определить характер
точек разрыва.
на непрерывность и определить характер
точек разрыва.
5. Найти производные функций и для одной из них найти дифференциал.
а)
![]() в)
в)
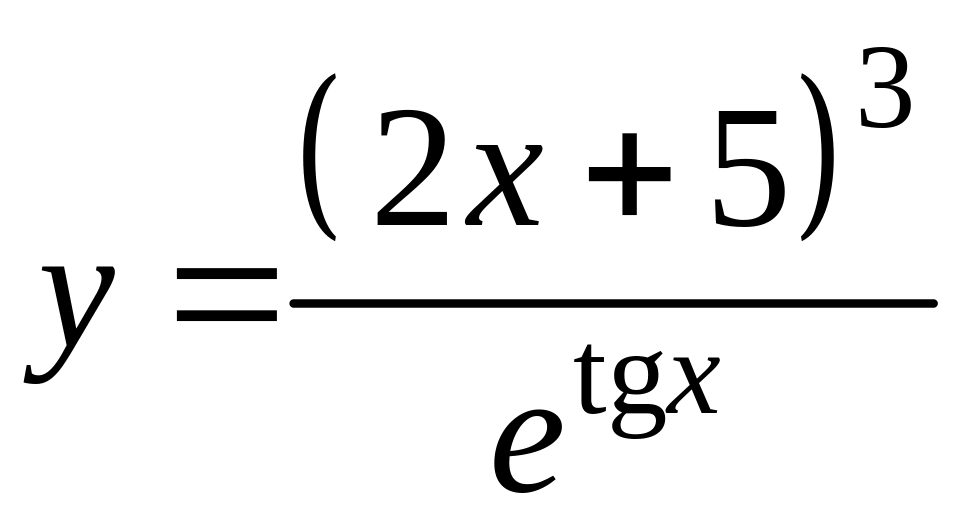
б)
![]() г)
г)
![]()
6. Найти и :
а)![]() ; б)
; б)
7. Записать уравнения касательной и
нормали к кривой
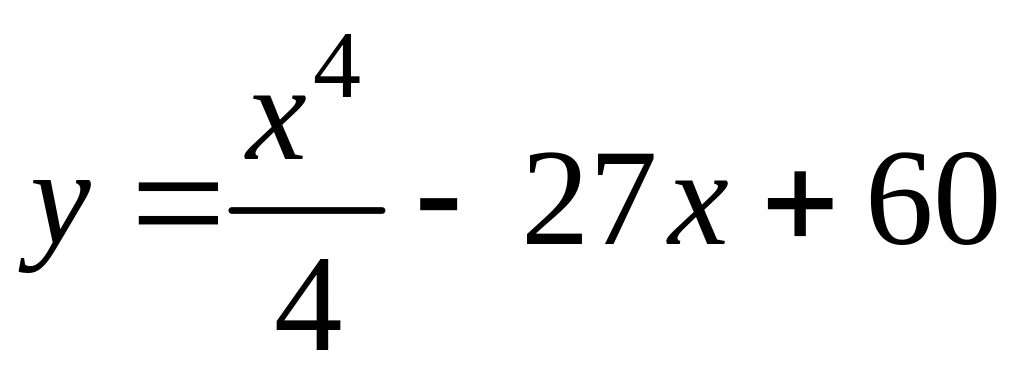 в точке с абсциссой
.
в точке с абсциссой
.
8. Вычислить с помощью дифференциала
приближенное значение функции
![]() при
при
![]() .
.
9. Используя правило Лопиталя, вычислить
![]() .
.
10. Найти частные производные первого порядка следующих функций:
а)
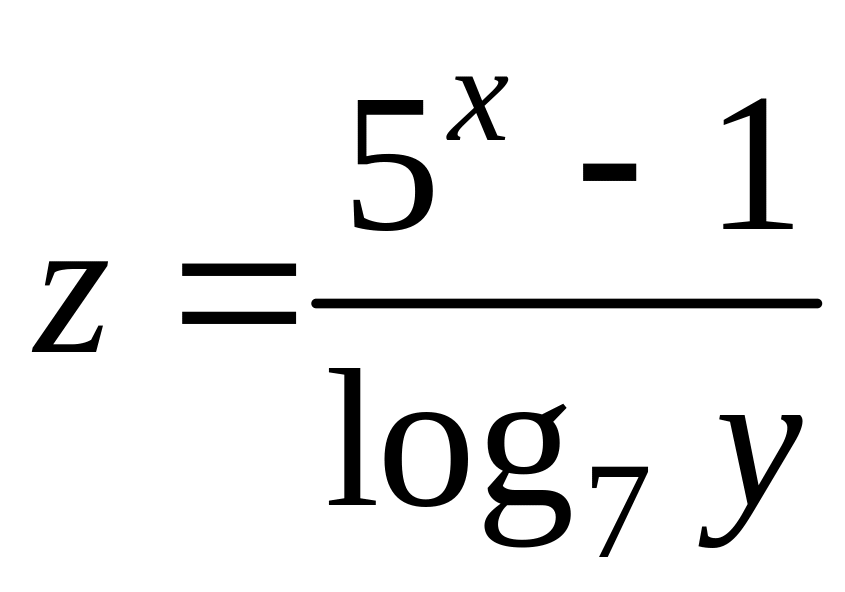 ; б)
; б)
![]() ; в)
; в)
![]() .
.
11. Найти дифференциалы первого и второго
порядка функции
![]() .
.
12. Провести исследование функции
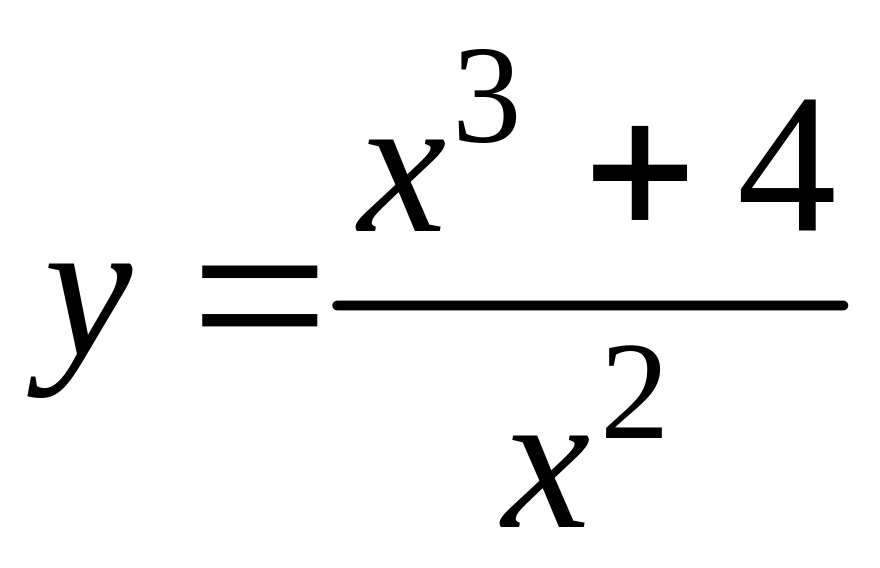 и построить ее график.
и построить ее график.
Вариант №12
1. Найти область определения функции
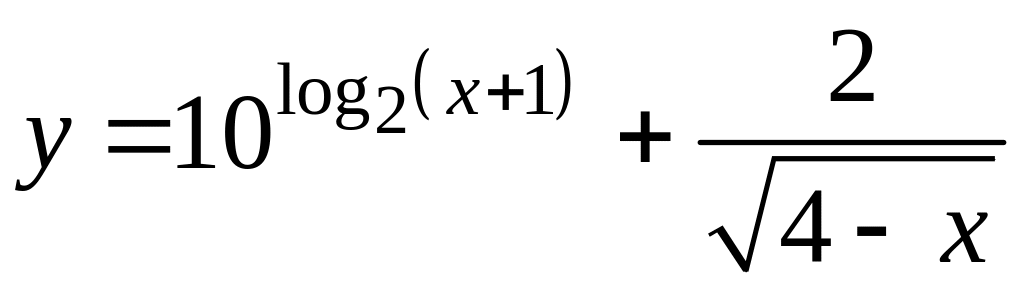 .
.
2. Построить область определения функции
![]() .
.
3. Найти пределы функций, не используя правило Лопиталя.
а)
; в)
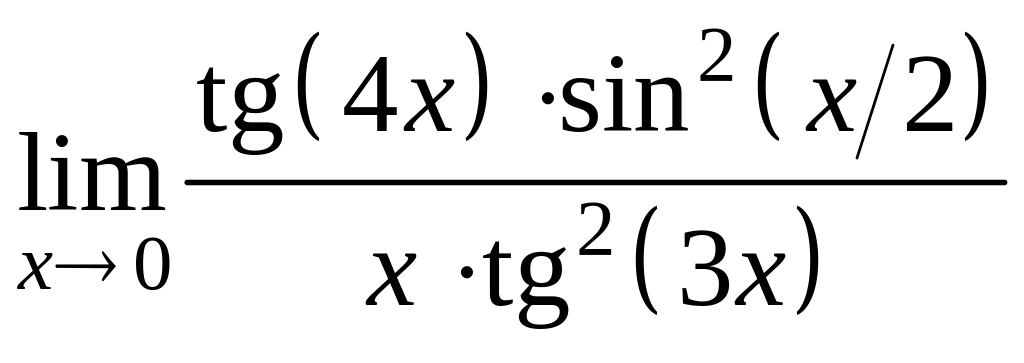 ;
;
б)
; г)
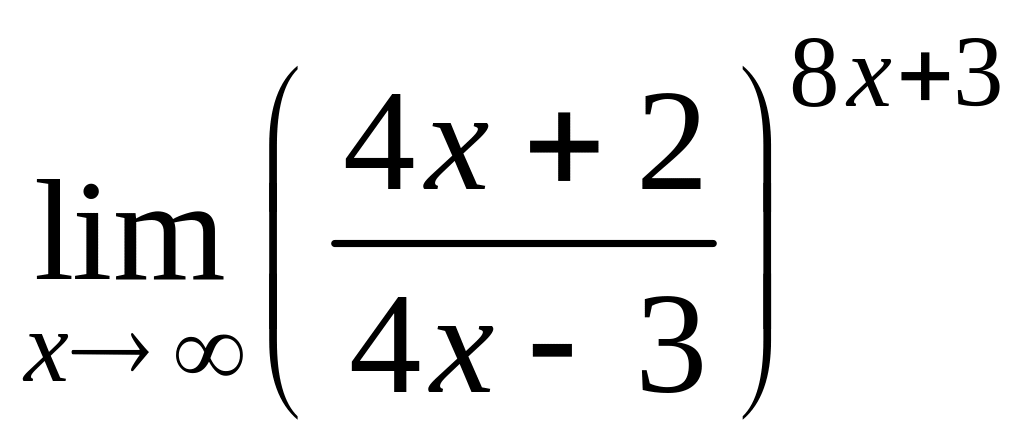 .
.
4. Исследовать функцию
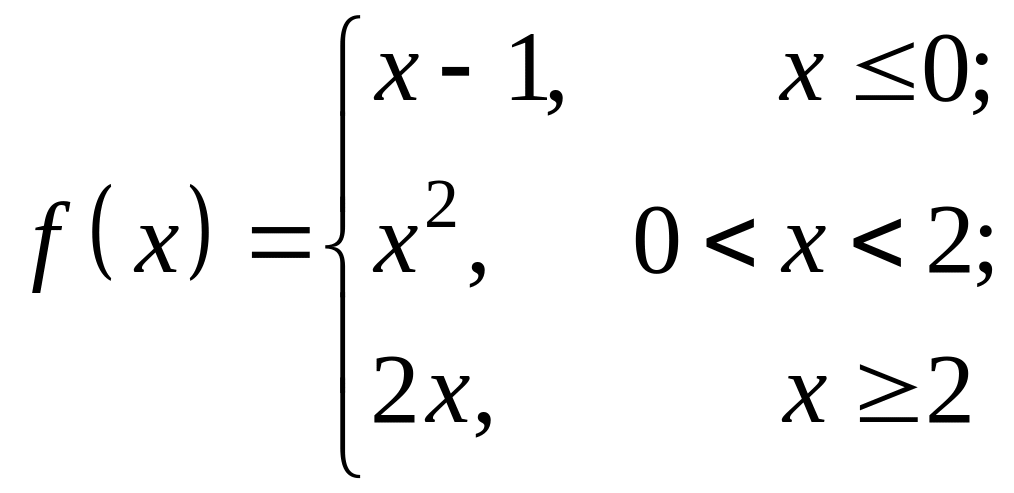 на непрерывность и определить характер
точек разрыва.
на непрерывность и определить характер
точек разрыва.
5. Найти производные функций и для одной из них найти дифференциал.
а)
![]() в)
в)
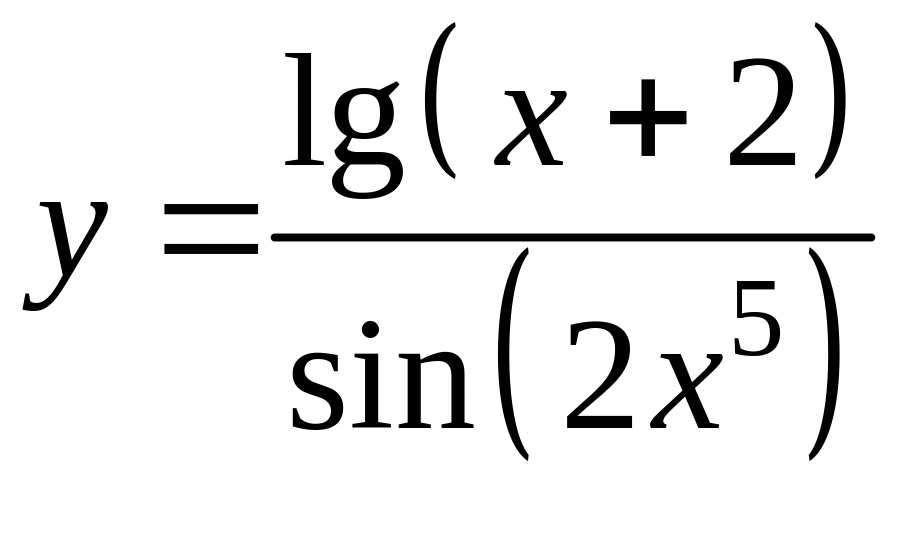
б)
![]() г)
г)
![]()
6. Найти и :
а)
![]() ; б)
; б)
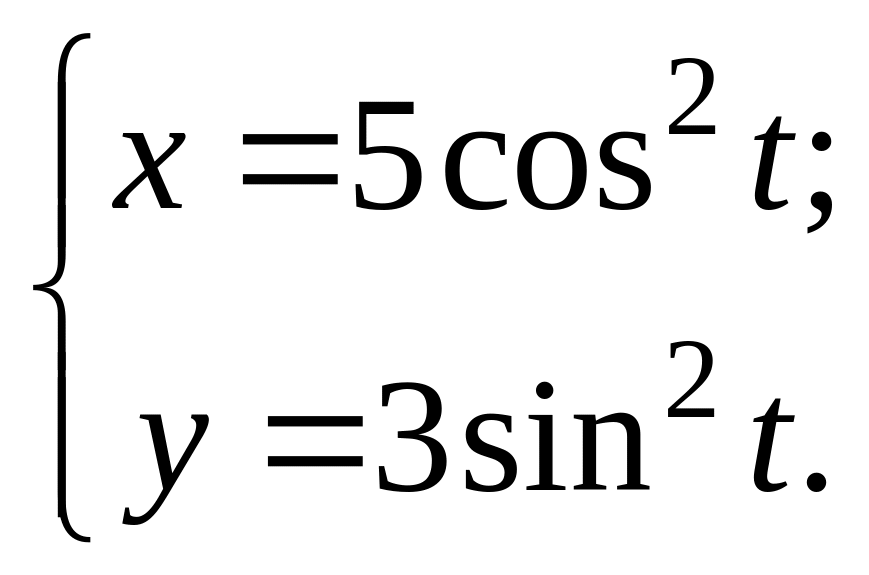
7. Записать уравнения касательной и
нормали к кривой
![]() в точке с абсциссой
в точке с абсциссой
![]() .
.
8. Вычислить с помощью дифференциала
приближенное значение функции
![]() при
при
![]() .
.
9. Используя правило Лопиталя, вычислить
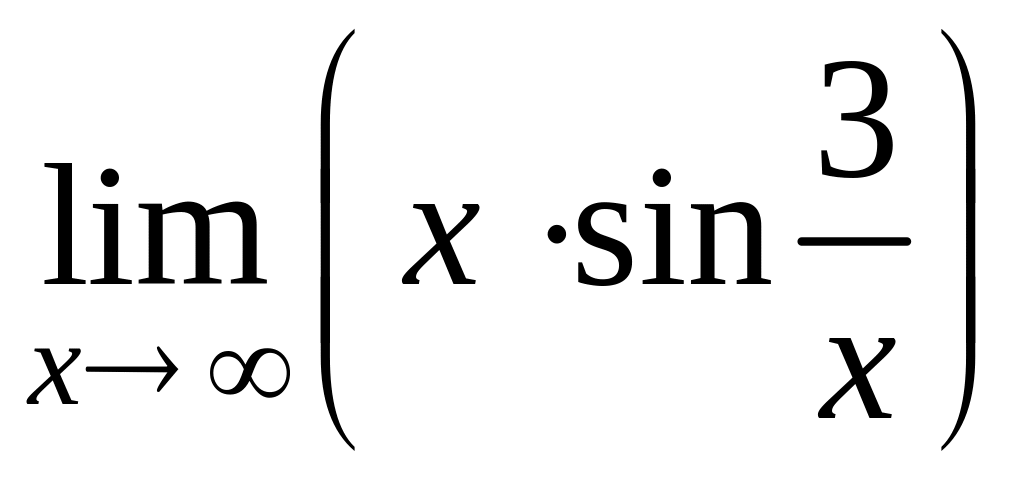 .
.
10. Найти частные производные первого порядка следующих функций:
а)
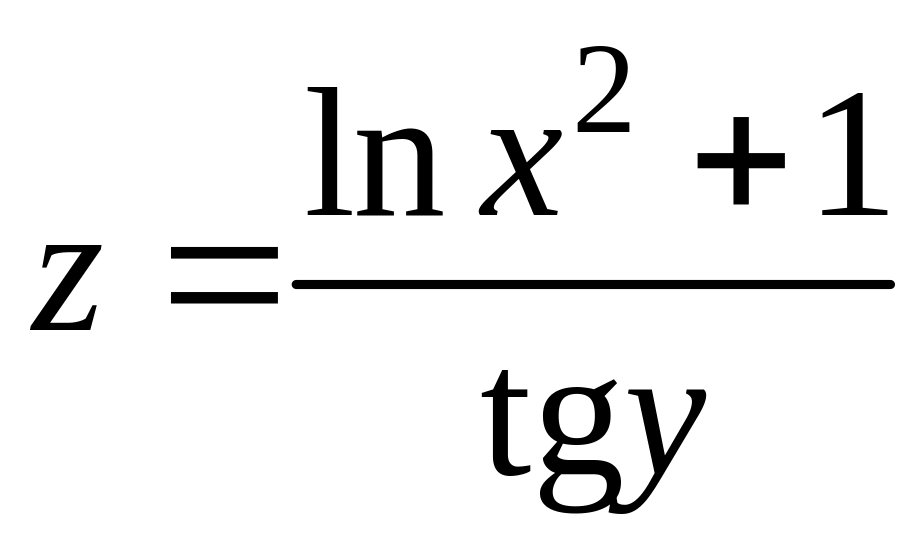 ; б)
; б)
![]() ; в)
; в)
![]() .
.
11. Найти дифференциалы первого и второго
порядка функции
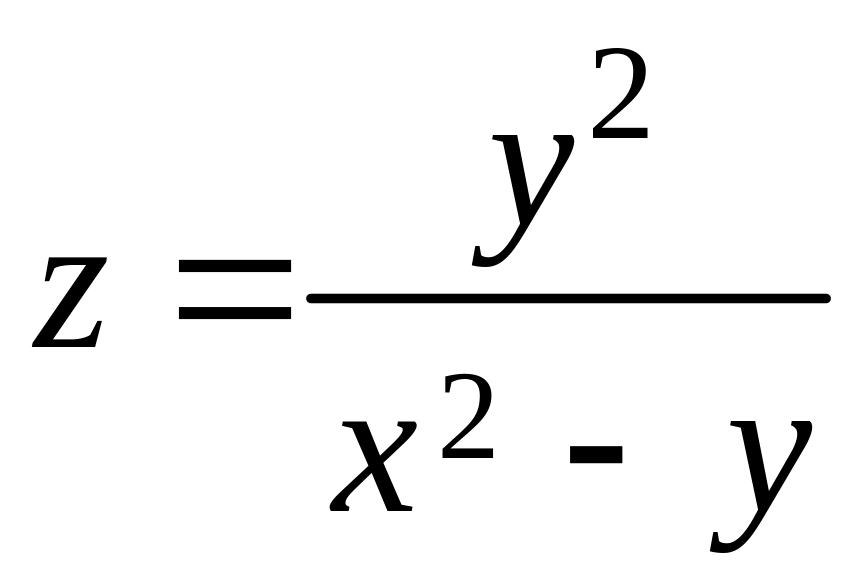 .
.
12. Провести исследование функции
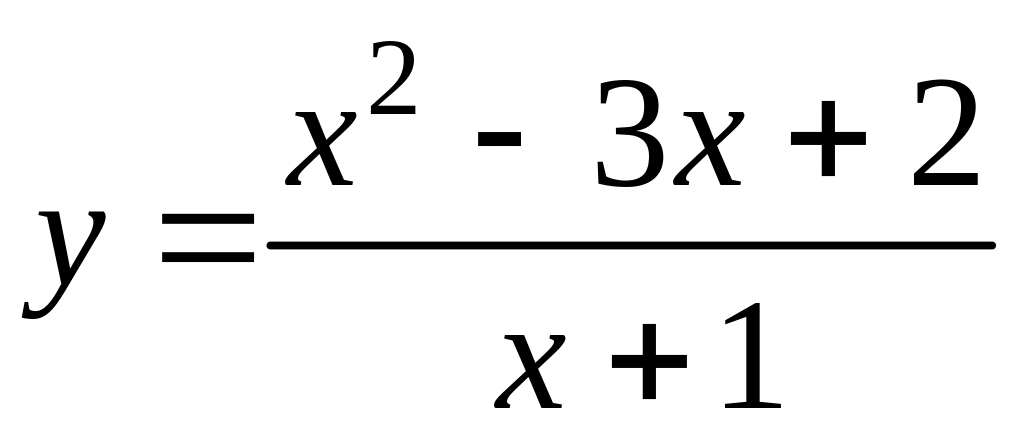 и построить ее график.
и построить ее график.
