3. Методика ознайомлення з конкретним змістом дії ділення на рівні частини.

Підготовча робота – практичні вправи на ділення на рівні частини і на вміщення.

Ознайомлення з конкретним змістом дії ділення

Після вивчення таблиці множення числа 2, учні знайомляться спочатку з конкретним змістом дії ділення на рівні частини, зі знаком дії ділення і читанням прикладів на ділення. Учням пропонується за­дача:

«6 яблук розділили порівну між двома учнями. Скільки яблук отримав кожний учень?» Ця задача розв'язується практично і вони отримають відповідь задачі.

Але записати розв'язок задачі вони ще не вміють. Тому учитель пояснює, що такі задачі розв'язуються дією ділення, показує знак ді­лення, записує розв'язок і з'ясовує, як слід читати цей запис.

Дві крапки (:) - знак ділення.

Приклади на ділення читають так:

шість поділити на два, дорівнює три.

Далі вчитель звертає увагу дітей, що в цій задачі яблука ділили порівну, тому її коротко можна записати наступним чином:

розділити на , порівну - ?

З метою закріплення отриманих знань, учні читають приклади на ділення.

4. Методика ознайомлення із взаємозв’язком дій множення і ділення, зв’язком між компонентами і результатом дій (знаходження невідомого компоненту).

Ознайомлення із взаємозв’язком дій множення і ділення

На наступному уроці учні знайомляться із взаємозв'язком між ді­ями множення і ділення.

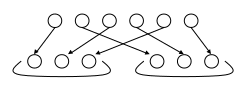
Учням пропонується розглянути малюнки і пояснити, які задачі складено за кожним малюнком:

2 • 5 = 10

10 : 2 = 5 10 : 5 = 2

Учні складають такі задачі:

1. 10 ґудзиків пришили у два ряди, порівну у кожному. Скільки ґу­дзиків в одному ряду?

2. 10 ґудзиків пришили у п'ять стовпчиків, порівну у кожному. Скі­льки ґудзиків в одному стовпчику?

Висновок: з кожного прикладу на множення можна скласти два приклади на ділення.

У 3 класі.

Повторення назви чисел дії множення, ділення, складання із прикладів на множення прикладів на ділення. Новим є те, що висновок узагальнюється. Якщо добуток двох чисел поділити на один із множників, то дістанемо другий множник. Надалі можемо перейти до формулювання правила знаходження невідомого множника.

Знаходження діленого пояснюється так:

20 : 4 = 5

ділене дільник частка

Поясни, що дістанемо, якщо дільник 4 помножити на частку 5. 4 • 5 = 20. Як знайти невідоме ділене? (Правило)

Знаходження дільника пояснюється аналогічно.

5. Методика ознайомлення з дією ділення на вміщення.

На наступному уроці, за підручником М.В. Богдановича, діти складають таблицю ділення на 2; і лише далі вводяться у порівнянні два види ділення: ділення на рівні частини і ділення на вміщен­ня.

Ознайомлення з дією ділення на вміщення. У підручнику М.В. Богдановича здійснюється на задачах: порівняй розв'язання і від­повіді задач:

1. Було 12 морквин. Моркву поділили на три рівні частини і зв'язали в пучки. Скільки морквин у кожному пучку?

12 : 3 = 4 (м.)

Відповідь: 4 морквини.

Це задача на ділення на рівні частини.

2. Було 12 морквин. Морквини поділили по три і зв'язали в пучки. Скільки вийшло пучків?

Ця задача розв'язується практично:

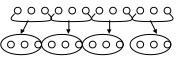
• В цій задачі ми 12 морквин ділили по 3 морквини; в 12 вміщується по 3 4 рази. Ця задача так само розв'язується дією ділення.

• Яким знаком позначається дія ділення? Ділення записується зна­ком «:» - «двокрапка».

12 : 3 = 4. Відповідь: 4 пучки.

• Цей запис читаємо так: 12 поділити по 3, отримаємо 4, або у 12 вміщується по 3 4 рази.

• У дужках нічого не пишемо, тому що ми отримали, що 4 рази вмі­щується у 12 по 3, і лише після цього зробили висновок про кіль­кість пучків.

Далі дітям пропонуються порівняти задачі на два види ділення: на рівні частини і на вміщення. Учні читають першу задачу, роз­повідають про що йде мова в задачі: що було, що зробили, про що за­питується в задачі. Учитель звертає увагу учнів на речення «Моркву - поділили на три рівні частини і зав'язали в пучки.», і запитує «Що оз­начає зміст цього речення?». Учні з'ясовують, що моркву поділили порівну на 3 частини-пучки, тобто у кожному пучку однакова кількість моркви. В тексті другої задачі звертаємо увагу на речення «Морквини поділили по три і зв'язали в пучки.» З'ясовуємо зміст цього речення: морквини поділили на кілька частин, причому в кожній час­тині по 3 морквини.

Порівнюємо тексти обох задач: з'ясовуємо, чим вони схожі і чим відрізняються. (Схожі - в них однакові числа і схожа ситуація; відрі­зняються змістом ділення: в першій задачі моркву розділили на три рівні частини і ми знайшли скільки морквин у кожній частині, а другій задачі моркву теж розділили на частини але, на відміну від попере­днього разу - по три штуки, і ми дізналися, скільки отримали таких частин.) Потім порівнюємо розв'язання цих задач - вони однакові, але в першій задачі ми отримали 4 морквини, тому що ми 12 морквин діли­ли на 3 рівні частини і дізналися, що в кожній такій частині по 4 морк­вини; а в другій задачі ми отримали відлучене число 4,тому що ми 12 морквин ділили по 3 морквини і дізналися, що 4 рази вміщується в 12 морквинах по 3 морквини.

Далі учитель пропонує з'ясувати, що в тексті задачі визначає вид ділення. Якщо в задачі говориться про те, що розкладали, розсипали, розрізали... по... - слід виконати ділення на вміщення; якщо в задачі говориться про те, що розкладали, розсипали, розрізали... порівну... - слід виконати ділення на рівні частини. Цей висновок можна оформи­ти засобом спареної конструкції:

Якщо в задачі говориться про те, що щось розкладали,

розсипали, розрізали… , то слід виконати дію ділення на .

Обидві задачі на дію ділення, їх опорні схеми:

розділили на порівну - ?

вміщується по - ?

На наступному уроці діти знайомляться з назвою компонентів і результату дії ділення:

частка

14 : 2

= 7

ділене

дільник

частка

Корисно підкреслити, що у дій додавання і множення, відні­мання і ділення багато спільного. По-перше, спільне можна побачити у назвах компонентів цих дій: при додаванні і множенні, компоненти з якими виконують ці дії називаються однаково, лише кажуть про порядок:перший - , другий - , а при відніманні і діленні - по різному: більше число, яке зменшується в результаті віднімання і ділення називають - , а число, яке віднімають або на яке ділять - називають відповідно тієї дії, що виконують - .

Для закріплення назв чисел при діленні учням пропонуються вправи:

1. Назви числа при діленні у прикладах:

16 : 2 = 8 51 : 17 = 3

2. Прочитай приклади на ділення з назвою компонентів і результатів арифметичних дій:

21 : 3 = 7 64 : 16 = 4