Министерство общего и профессионального образования Российской Федерации

Томский государственный университет систем управления и радиоэлектроники (тусур)

Кафедра промышленной электроники (ПрЭ)

Информатика 4 Курсовой проект

Вар 13

Преподаватель Студент группы

___________ /____________. / __ ___________ /

___________200_ г. ____ ______ 200_ г.

Техническое задание

Необходимо найти минимум функции в заданной области.

При выполнении данного проекта необходимо учитывать, что решение задачи является подверженным влиянию случайных величин. Поэтому каждый запуск программы необходимо повторять, по крайней мере, 2030 раз. После этого из набора полученных решений надо отобрать лучшее. Разумеется, это надо сделать, поместив содержание главной программы в соответствующий цикл, в котором будет одновременно выбираться наилучшее решение. Одновременно надо вычислить и среднее значение минимума за эти 20-30 прогонов.

Рассмотреть двухточечное скрещивание и двухточечную мутацию.

Каждая переменная кодируется 20 битами.

Провести расчеты для 40 и 80 поколений.

Сравнить получающиеся решения при размерах популяции 8, 12, 20 особей.

Содержание

Техническое задание 2

Анализ вариантов решения задачи 4

Описание и обоснование выбранного варианта 11

Результаты эксперимента 16

Выводы 17

Список литературы 18

Приложение А 20

Анализ вариантов решения задачи

Генетические Алгоритмы - адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы.

В природе особи в популяции конкурируют друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Те особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень немногочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространятся в увеличивающемся количестве потомков на каждом последующем поколении. Комбинация хороших характеристик от различных родителей иногда может приводить к появлению "суперприспособленного" потомка, чья приспособленность больше, чем приспособленность любого из его родителя. Итак, вид развивается, лучше и лучше приспосабливаясь к среде обитания.

ГА используют прямую аналогию с таким механизмом. Они работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Например, мерой приспособленности могло бы быть отношение силы/веса для данного проекта моста. (В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы.) Наиболее приспособленные особи получают возможность "воспроизводить" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции.

Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге, популяция будет сходиться к оптимальному решению задачи.

Имеются много способов реализации идеи биологической эволюции в рамках ГА. Традиционным считается ГА, представленный на рисунке 1.

НАЧАЛО /* генетический алгоритм */ Создать начальную популяцию Оценить приспособленность каждой особи останов := FALSE ПОКА НЕ останов ВЫПОЛНЯТЬ НАЧАЛО /* создать популяцию нового поколения */ ПОВТОРИТЬ (размер_популяции/2) РАЗ НАЧАЛО /* цикл воспроизводства */ Выбрать две особи с высокой приспособленностью из предыдущего поколения для скрещивания Скрестить выбранные особи и получить двух потомков Оценить приспособленности потомков Поместить потомков в новое поколение КОНЕЦ ЕСЛИ популяция сошлась ТО останов := TRUE КОНЕЦ КОНЕЦ

Рис.1.1. Псевдокод

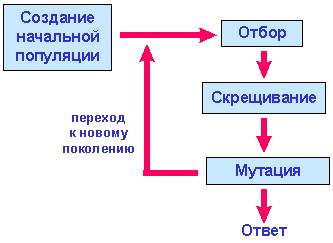
Рис.1.2. Блок-схема генетического алгоритма

Рис.1. Схема генетического алгоритма

В последние годы реализовано много генетических алгоритмов и в большинстве случаев они мало похожи на этот ГА. По этой причине в настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов, подчас мало похожих друг от друга. Исследователи экспериментировали с различными типами представлений, операторов кроссовера и мутации, специальных операторов, и различных подходов к воспроизводству и отбору.

Генетический алгоритм включает три операции: селекция, скрещивание, мутация.

Оператор селекции (reproduction, selection) осуществляет отбор хромосом в соответствии со значениями их функции приспособленности. Существуют как минимум два популярных типа оператора селекции: рулетка и турнир.

• Метод рулетки (roulette-wheel selection) - отбирает особей с помощью n "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции.

Размер i-ого сектора пропорционален соответствующей величине P_sel(i) вычисляемой по формуле:

При таком отборе члены популяции с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью.

Рис. 2. Оператор селекции типа колеса рулетки с пропорциональными функции приспособленности секторами

• Турнирный отбор (tournament selection) реализует n турниров, чтобы выбрать n особей. Каждый турнир построен на выборке k элементов из популяции, и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k=2.

В данной работе реализован турнирный отбор.

Для выполнения отбора используются вспомогательные подпрограммы – процедура shuffle, «перемешивающая» популяцию (меняющая местами особи) и функция select1, выбирающая одну более приспособленную особь из двух (сравниваются соседние особи, когда достигнут конец популяции – они перемешиваются и отбор начинается с первой особи). Основная процедура select осуществляет отбор требуемого количества особей за счет вызова функции select1 внутри цикла.

Скрещивание представляет собой процесс случайного обмена значениями соответствующих элементов для произвольно сформированных пар строк. Для этого выбранные на этапе воспроизводства строки случайным образом группируются в пары. Далее каждая пара с заданной вероятностью p_скр подвергается скрещиванию.

Схема скрещивания представлена на рисунке 3.

Рис. 3. Схема скрещивания

При скрещивании происходит случайный выбор позиции разделителя d (d=1, 2, ..., l-1, где l - длина строки). Затем значения первых d элементов первой строки записываются в соответствующие элементы второй, а значения первых d элементов второй строки - в соответствующие элементы первой. В результате получаем две новых строки, каждая из которых является комбинацией частей двух родительских строк.

Наряду с одноточечным может быть рассмотрено многоточечное скрещивание. Частным случаем многоточечного скрещивания является двухточечное скрещивание, рассмотренное в данной работе.

Мутация представляет собой процесс случайного изменения значений элементов строки. Для этого строки, получившиеся на этапе скрещивания, просматриваются поэлементно, и каждый элемент с заданной вероятностью мутации p_мут может мутировать, т.е. изменить значение на любой случайно выбранный символ, допустимый для данной позиции. В случае, когда элемент может принять только одно из двух значений (0 и 1, истина и ложь) говорят об инверсионной мутации – значение может измениться только на противоположное, т.е. происходит инверсия. Кроме инверсионной, бывает двухточечная мутация, когда два случайно выбранных элемента обмениваются значениями.

Операция мутации позволяет находить новые комбинации признаков, увеличивающих ценность строк популяции.