5.3. Задачи на циклические алгоритмы с известным количеством повторений

5.3.1. Найти сумму первых N четных натуральных чисел.

5.3.2. Получить первые N чисел Фибоначчи: а₁ = а₂ = 1, а_з = а₁ + а₂ = 2, а₄ = а₂ + а_з = 3 и т.д.

5.3.3. Последовательно вводятся N целых чисел. Найти сумму всех положительных среди них.

5.3.4. Последовательно вводятся N целых чисел. Найти количество отрицательных среди них.

5.3.5. Последовательно вводятся N целых чисел. Определить, каких среди них чисел больше: положительных или отрицатель­ных.

5.3.6. Последовательно вводятся N целых чисел. Найти максималь­ное из них.

5.3.7. Последовательно вводятся N целых чисел. Найти минималь­ное из них.

5.3.8. Последовательно вводятся N целых чисел. Сосчитать, сколько из них совпадают с первым числом.

5.3.9. Последовательно вводятся N целых чисел. Найти разницу между наибольшим и наименьшим из них.

5.3.10. Последовательно вводятся N целых чисел. Найти cpeднее арифметическое этих чисел.

5.3.11. Найти наибольший общий делитель двух чисел А и В (алгоритм Евклида: НОД=m, если m=n. Иначе при m>n m=m–n, при n>m n=n–m).

5.3.12. Найти наименьшее общее кратное двух чисел А и В.

5.3.13. Найти сумму чисел 1, 1/2, 1/3, 1/4 и т.д., больших заданного числа А.

5.3.14. Вычислить y=

где а = mn – 5; b = m + n.

5.3.15. Если сумма двух чисел больше 10, то наибольшее из них заменить их произведением, иначе – частным.

5.4. Задачи на циклические алгоритмы с выходом из цикла по условию

5.4.1. Дано действительное число E, у₀, у_k = 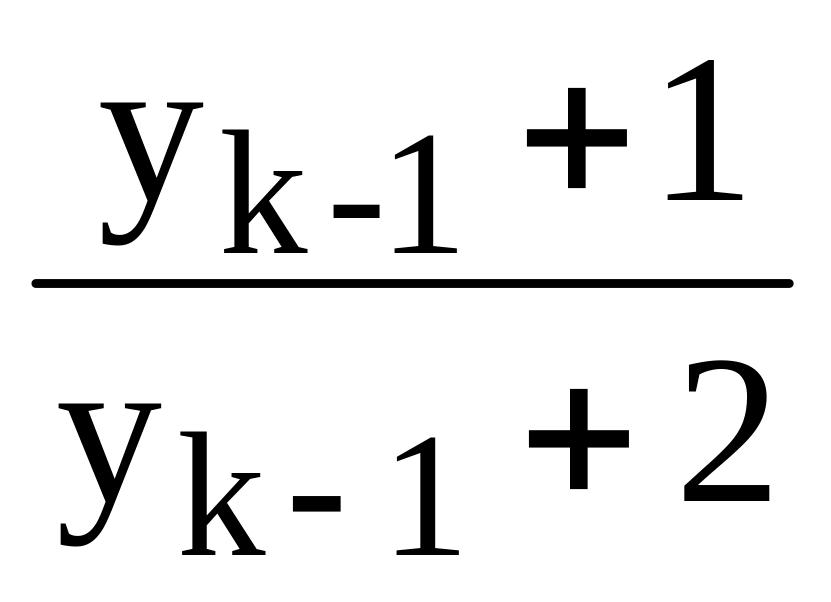, k=1, 2, 3, …

Найти первый член у_n, для которого выполнено условие .

5.4.2. Вычислить . Процесс суммирования закончить, если |U_n|= , где Е и х – заданные действительные числа.

5.4.3. Вычислить , для значений |x|<1. Процесс суммирования закончен, если |U_n|= , где Е и х – заданные действительные числа.

5.4.4. Дано положительное число E, x₀=1, x_k=(2 – )/5, k=1, 2, … . Найти первый член x_k и его порядковый номер, для которого |x_k – x_k-1|<E.

5.4.5. Вычислить сумму с точностью Е. Считать, что точность достигнута, если вычислена сумма нескольких слагаемых и очередное слагаемое оказалось по модулю меньше, чем Е. Это и последующее слагаемое в сумме не учитывать.

5.4.6. Задание аналогично п.5.4.5. Вычислить сумму с точностью Е.

5.4.7. Задание аналогично п.5.4.5. Вычислить сумму , где |x|<1 с точностью Е.

5.4.8. Задание аналогично п.5.4.5. Вычислить сумму, где 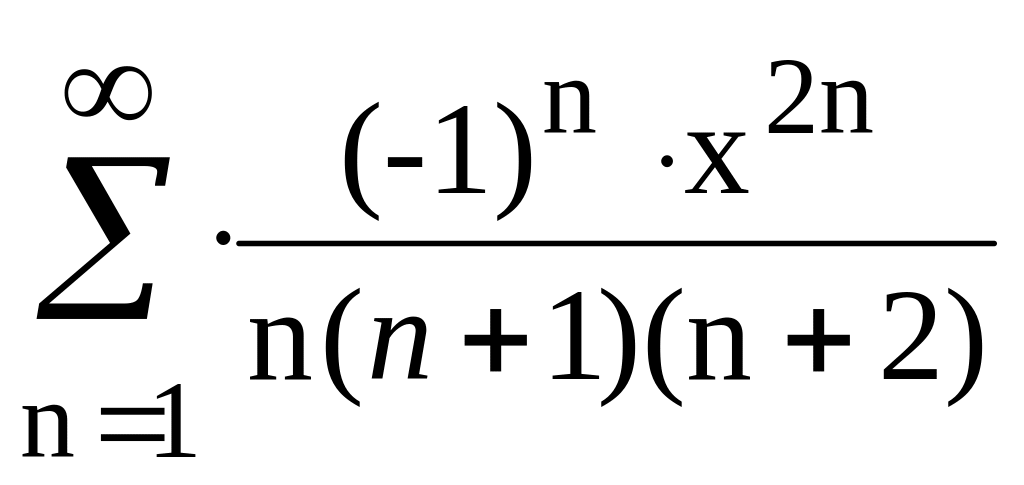, где 0,2<|x|<0.7 с точностью Е.

5.4.9. Дано действительное число Е и x₀=5, x₁=1. . Найти два значения x_k и x_k-1, для которых |x_k – x_k-1|<E.

5.4.10. Пусть a₁=b₁=1, a_k=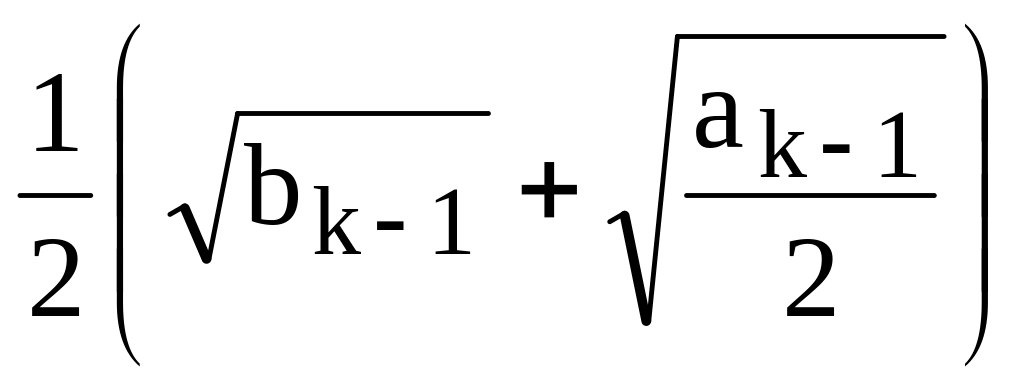 , b_k=2a +b_k-1, k=2, 3, 4,… . Найти k, для которого 2< <3.

5.4.11. Пусть V1=V2=0, V3=1.5; V_i= , i = 4, 5, 6,… .. Найти три последовательных числа. V_i, V_i+1, V_i+2, что |V_i|>20.

5.4.12. Вычислить сумму cos1+cos2+cos3+… . Окончание итерационного процесса тогда, когда |cosi+cos(i+1)+cos(i+2)|>0,3. Вывести значение суммы.

5.4.13. Найти значение числа n для числовой последовательности, заданной рекуррентным соотношением

y_n=2y_n-1+y_n-2+200, если y₁=-150 y₂=-140, если |y_n|>1000.

5.4.14. Дано число B>0. Необходимо вводить действительные числа y1, y2, y3,… , пока сумма модулей введенных чисел будет меньше В. Определить их среднее арифметическое.

5.4.15. Вычислить сумму , где 0,1<|x|<0,4. Процесс суммирования продолжать до тех пор, пока , где Е, х – данные действительные числа.