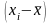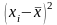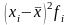Вариант 10

Задача 1. Имеются следующие данные о стаже работы и среднемесячной заработной плате рабочих-сдельщиков.

№ п/п	Стаж работы, лет	Месячная заработная плата, тыс. руб.	№ п/п	Стаж работы, лет	Месячная заработная плата, тыс. руб.
1	1	6,50	11	12,0	7,96
2	6,5	7,02	12	10,5	7,88
3	9,2	7,95	13	9,0	7,87
4	4,5	7,04	14	5,0	7,82
5	6,0	7,20	15	10,2	7,90
6	2,5	6,92	16	5,0	7,08
7	2,7	7,00	17	5,4	7,25
8	16,8	8,18	18	7,5	7,85
9	14,0	8,10	19	8,0	7,90
10	11,0	8,11	20	8,5	7,98

Для выявления зависимости между стажем работы и месячной заработной платой сгруппируйте рабочих-сдельщиков по стажу, образовав труппы с равными интервалами.

Результаты представьте в табличной форме.

Решение:

Построим ряд распределения рабочих по стажу работы.

Количество групп определим по формуле Стерджесса:

N=1+3,322*lg20=5,3

Примем число групп равное 5

Величину интервала определим по формуле:

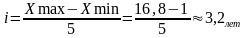
_{где xmax, xmin – максимальное и минимальное значения признака.}

Распределим рабочих по группам.

Таблица 1.1 – Вспомогательная таблица

Группы рабочих по стажу работы, лет	№ п/п	Стаж работы, лет	Месячная заработная плата, тыс. руб.
1-4,2	1	1	6,5
	6	2,5	6,92
	7	2,7	7
Итого по группе	3	6,2	20,42
4,2-7,4	4	4,5	7,04
	14	5	7,82
	16	5	7,08
	17	5,4	7,25
	5	6	7,2
	2	6,5	7,02
Итого по группе	6	32,4	43,41
7,4-10,6	18	7,5	7,85
	19	8	7,9
	20	8,5	7,98
	13	9	7,87
	3	9,2	7,95
	15	10,2	7,9
	12	10,5	7,88
Итого по группе	7	62,9	55,33
10,6-13,8	10	11	8,11
	11	12	7,96
Итого по группе	2	23	16,07
13,8-16,8	9	14	8,1
	8	16,8	8,18
Итого по группе	2	30,8	16,28
Всего	20	155,3	151,51

По каждой группе рассчитаем стаж работы и месячную заработную плату в среднем на одного рабочего.

Таблица 1.2 – Распределение рабочих по стажу работы.

Группы рабочих по стажу работы, лет	Число рабочих, чел.	Стаж работы, лет		Месячная заработная плата, тыс. руб.
		В целом по группе	В среднем на 1 рабочего	В целом по группе	В среднем на 1 рабочего
1-4,2	3	6,2	2,1	20,42	6,8
4,2-7,4	6	32,4	5,4	43,41	7,2
7,4-10,6	7	62,9	9,0	55,33	7,9
10,6-13,8	2	23	11,5	16,07	8,0
13,8-16,8	2	30,8	15,4	16,28	8,1
Всего	20	155,3	7,8	151,51	7,6

Вывод: Видим, что в расчете на одного рабочего-сдельщика месячная заработная плата увеличивается с увеличением стажа работы. Значит, между стажем работы и месячной заработной платой существует прямая зависимость.

Задача 2. По данным переписи населения Российской Федерации 2002 г. имеются следующие данные о возрасте населения:

Группы населения по возрасту, лет	Мужчины, в % к итогу.	Женщины, в % к итогу
0-5	4,8	4,0
5-10	5,2	4,4
10-15	7,9	6,6
15-20	9,6	8,1
20-25	8,6	7,3
25-30	7,9	6,8
30-35	7,3	6,4
35-40	7,4	6,7
40-45	9,0	8,3
45-50	8,1	7,9
50-55	6,9	7,0
55-60	3,5	3,8
60-65	4,8	6,1
65-70	3,6	5,0
70 и более	5,4	11,6
Итого	100,0	100,0

Определить:

1. Средний возраст мужчин и женщин.

Решение:

Среднее значение определяется по формуле средней арифметической взвешенной:

,

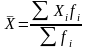где x – значения признака;

f – частота повторения значений признака.

В случае, если ряд интервальный, его нужно превратить в условно дискретный: в качестве группового значения x_i для каждого интервала вычисляется его середина:

,

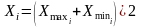где, Xmin , X max– нижняя и верхняя граница i –го интервала в ряду распределения.

Для расчетов используем вспомогательную таблицу.

Таблица 2.1 – Расчет среднего возраста

Группы населения по возрасту, лет	Середина интервала x	Мужчины, в % к итогу. f	x*f	Женщины, в % к итогу f	x*f
0-5	2,5	4,8	12	4	10
5-10	7,5	5,2	39	4,4	33
10-15	12,5	7,9	98,75	6,6	82,5
15-20	17,5	9,6	168	8,1	141,75
20-25	22,5	8,6	193,5	7,3	164,25
25-30	27,5	7,9	217,25	6,8	187
30-35	32,5	7,3	237,25	6,4	208
35-40	37,5	7,4	277,5	6,7	251,25
40-45	42,5	9	382,5	8,3	352,75
45-50	47,5	8,1	384,75	7,9	375,25
50-55	52,5	6,9	362,25	7	367,5
55-60	57,5	3,5	201,25	3,8	218,5
60-65	62,5	4,8	300	6,1	381,25
65-70	67,5	3,6	243	5	337,5
70 и более	72,5	5,4	391,5	11,6	841
Итого	-	100	3508,5	100	3951,5

Рассчитаем средний возраст мужчин:

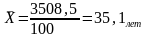
Рассчитаем средний возраст женщин:

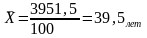
Вывод: Из проведенных расчетов видим, что средний возраст женщин больше среднего возраста мужчин.

Задача 3. Используя условие задачи 2, проанализируйте надежность исчисленного возраста населения РФ, вычислив показатели вариации: дисперсию, среднее квадратическое отклонение и коэффициент вариации.

Решение:

Дисперсия (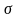 ²) определяется по формуле:

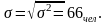
Среднее квадратическое отклонение:

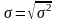
Коэффициент вариации определяется

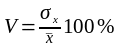
При вычислении указанных показателей расчеты удобнее произвести в таблице

Таблица 3.1 – Вспомогательные расчеты (для мужчин)

Группы населения по возрасту, чел.	Мужчины, в % к итогу. f	Центральное значение интервала (xi)
0-5	4,8	2,5	-32,6	1062,76	5101,248
5-10	5,2	7,5	-27,6	761,76	3961,152
10-15	7,9	12,5	-22,6	510,76	4035,004
15-20	9,6	17,5	-17,6	309,76	2973,696
20-25	8,6	22,5	-12,6	158,76	1365,336
25-30	7,9	27,5	-7,6	57,76	456,304
30-35	7,3	32,5	-2,6	6,76	49,348
35-40	7,4	37,5	2,4	5,76	42,624
40-45	9	42,5	7,4	54,76	492,84
45-50	8,1	47,5	12,4	153,76	1245,456
50-55	6,9	52,5	17,4	302,76	2089,044
55-60	3,5	57,5	22,4	501,76	1756,16
60-65	4,8	62,5	27,4	750,76	3603,648
65-70	3,6	67,5	32,4	1049,76	3779,136
70 и более	5,4	72,5	37,4	1398,76	7553,304
Итого	100	-			38504,3

Дисперсия ( ²)

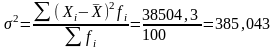
Среднее квадратическое отклонение:

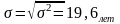
Коэффициент вариации

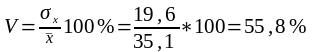
По полученным результатам сделаем следующие выводы. Среднее значение возраста мужчин по совокупности отличается от среднего на 27,9 лет. Коэффициент вариации 55,8% (то есть >33,3%),, значит, совокупность мужчин неоднородна по признаку среднего возраста.

Теперь проведем все расчеты для женщин.

Таблица 3.2 – Вспомогательные расчеты (для женщин)

Группы населения по возрасту, чел.	Женщины, в % к итогу. f	Центральное значение интервала (xi)
0-5	4	2,5	-37	1369	5476
5-10	4,4	7,5	-32	1024	4505,6
10-15	6,6	12,5	-27	729	4811,4
15-20	8,1	17,5	-22	484	3920,4
20-25	7,3	22,5	-17	289	2109,7
25-30	6,8	27,5	-12	144	979,2
30-35	6,4	32,5	-7	49	313,6
35-40	6,7	37,5	-2	4	26,8
40-45	8,3	42,5	3	9	74,7
45-50	7,9	47,5	8	64	505,6
50-55	7	52,5	13	169	1183
55-60	3,8	57,5	18	324	1231,2
60-65	6,1	62,5	23	529	3226,9
65-70	5	67,5	28	784	3920
70 и более	11,6	72,5	33	1089	12632,4
Итого	100	-			44916,5

Дисперсия ( ²)

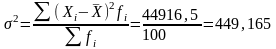
Среднее квадратическое отклонение:

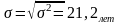
Коэффициент вариации

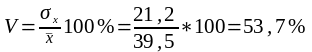
Вывод: Среднее значение возраста мужчин по совокупности отличается от среднего на 21,2 года. Коэффициент вариации 53,7% (то есть >33,3%),, значит, совокупность женщин неоднородна по признаку среднего возраста.

Задача 4. Туристическая компания предлагает места в гостиницах приморского курорта. Менеджера компании интересует, насколько возрастает привлекательность гостиницы в зависимости от ее расстояния до пляжа.

Расстояние, км.	Наполняемость, %
0,1	92
0,1	95
0,2	96
0,3	90
0,4	89
0,4	86
0,5	90
0,6	83
0,7	85
0,7	80
0,8	78
0,8	76
0,9	72
0,9	75

1. Постройте поле корреляции по фактическим данным. Определите характер зависимости.

2. Рассчитайте линейный коэффициент корреляции.

3. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Решение:

Построим поле корреляции.

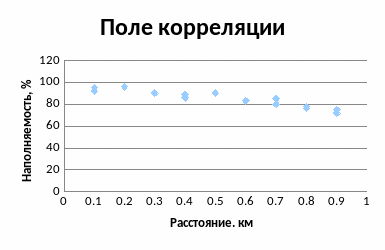
Рисунок 1 - Поле корреляции

Видим, что зависимость обратная. То есть, с увеличением расстояния от гостиницы до пляжа ее привлекательность снижается.

Для определения тесноты корреляционной связи применяют коэффициент корреляции:

Для расчетов построим таблицу

Таблица 4.1 Расчет коэффициента корреляции

№ п/п	Расстояние, км. X	Наполняемость, % Y	X2	XY	Y2
1	0,1	92	0,01	9,2	8464
2	0,1	95	0,01	9,5	9025
3	0,2	96	0,04	19,2	9216
4	0,3	90	0,09	27	8100
5	0,4	89	0,16	35,6	7921
6	0,4	86	0,16	34,4	7396
7	0,5	90	0,25	45	8100
8	0,6	83	0,36	49,8	6889
9	0,7	85	0,49	59,5	7225
10	0,7	80	0,49	56	6400
11	0,8	78	0,64	62,4	6084
12	0,8	76	0,64	60,8	5776
13	0,9	72	0,81	64,8	5184
14	0,9	75	0,81	67,5	5625
Итого	7,4	1187	4,96	600,7	101405

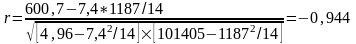
Значение коэффициента корреляции подтверждает. что связь между признаками обратная. То есть, с увеличением расстояния от гостиницы до пляжа ее привлекательность снижается.

Построим уравнение регрессии

Система нормальных уравнений имеет вид

na₀ + a₁X = Y ;

a₀X + a₁X² = XY

14*а₀+а₁*7,4=1187

а₀*7,4+а₁*4,96=600,7

Отсюда а₀=98,305, а₁=-25,556

Вывод: Следовательно уравнение имеет вид: Y_х = а₀ + a₁X, = 98,305 – 25,556Х

Задача 5. Численность населения Архангельской области (на начало года), тыс. чел составляла по годам:

Год	1995	1996	1997	1998	1999	2000	2001	2002
Население, тыс. чел.	1534,0	1520,2	1506,4	1491,9	1478,0	1459,2	1.442,7	1428,9

Проанализируйте динамику численности населения Архангельской области указанные годы. Сделайте вывод.

Решение:

Показатели динамики рассчитываются как базисные, так и цепные. Базисные - в сравнении с первым годом, цепные – в сравнении с предыдущим годом

Показатель	Базисный	Цепной
Абсолютный прирост (iбаз и iцеп)	Уi–У1	Уi–Уi-1
Темп роста (Т р)	Уi: У1 *100	Уi:Уi-1 *100
Темп прироста (Тпр)	Тр-100	Тр-100

Аналитические показатели ряда динамики представим в таблице.

Таблица 5.1

Анализ динамики численности населения Архангельской области

Год	Население. тыс.чел.	Абсолютный прирост, тыс.чел.		Темп роста, %		Темп прироста, %
		цепной	базисный	цепной	базисный	цепной	базисный
1995	1534,0			100	100
1996	1520,2	-13,8	-13,8	99,1	99,1	-0,9	-0,9
1997	1506,4	-13,8	-27,6	99,1	98,2	-0,9	-1,8
1998	1491,9	-14,5	-42,1	99,0	97,3	-1,0	-2,7
1999	1478,0	-13,9	-56	99,1	96,3	-0,9	-3,7
2000	1459,2	-18,8	-74,8	98,7	95,1	-1,3	-4,9
2001	1442,7	-16,5	-91,3	98,9	94,0	-1,1	-6,0
2002	1428,9	-13,8	-105,1	99,0	93,1	-1,0	-6,9

Средний уровень интервального ряда определяется по средней арифметической простой:

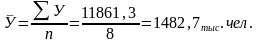
Средний абсолютный прирост можно рассчитать:

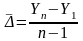
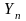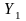где - последний уровень ряда;

- первый уровень ряда;

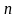- число уровней ряда.

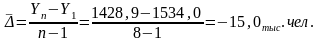
Среднегодовой темп роста определяется:

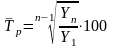
где п- число уровней ряда.

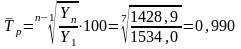
или 99,0%

Средний темп прироста:

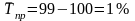
Вывод: По анализу ряда динамики можно сделать выводы. Население Архангельской области уменьшалось год от года. За 8 лет оно уменьшилось на 13,8 тыс.чел. или на 6,9%.. Среднегодовая численность населения за 8 лет составила 1482,7 тыс.чел., а среднегодовое снижение 15,0 тыс.чел. или 1%.

Задача 6. Индекс выпуска продукции и услуг базовых отраслей экономики РФ, в процентах к предыдущему году, составляет:

Год	1996	1997	1998	1999	2000	2001	2002	2003	2004
Выпуск продукции II услуг, % к предыдущему году	94,0	100,7	94,0	107,1	110,8	105,9	103,7	107,3	106,6

Определить, как изменился индекс выпуска продукции и услуг в 2004 году по сравнению с 1995годом.

Решение:

Рассчитаем изменение выпуска продукции и услуг с помощью формулы коэффициента роста, рассчитанного базисным способом.

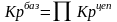
где 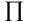- знак произведения.

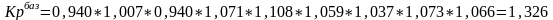или 132,6%

Вывод: Таким образом, выпуск продукции и услуг в 2004 году по сравнению с 1995 годом увеличился на 32,6%.