Правила границь функції

Якщо границі функцій F₁(x) і F₂(x)при х, що прямує до х₀ існують і є скінченними, то виконуються правила:

1. Границя суммы

Границя суми скінченого числа функцій дорівнює сумі границь доданків (якщо кожна з них існує) 

2. Границя добутку

Границя добутку скінченого числа функцій дорівнює добутку границь множників (якщо кожна з них існує)    Звідси - наступні дві властивості.

3. Границя добутку функції на константу

Постійний множник можна винести за знак границі 

4. Границя функції в натуральному ступені

Границя функції в натуральному ступені дорівнює натуральному ступеню від границі функції 

5. Границя відношення (дробу)

Границя відношення функцій дорівнює відношенню границь (якщо кожна з них існує і при цьому границя знаменника не дорівнює нулю) 

Для того щоб знайти границю елементарної функції, коли аргумент прямує до значення, що належить області визначення функції, треба замість аргумента в вираз підставити граничне значення аргументу. Це правило називається правилом граничного переходу.

Границі функції застосовують для знаходження асимптот графіка функції:

Пряма х = А є вертикальною асимптотою, якщо границя цієї функції дорівнює нескінченності при аргументі, що прямує до А.

Пряма у = В є горизонтальною асимптотою, якщо границя цієї функції дорівнює числу В при аргументі, що прямує до нескінченності.

Пряма y = kx + b є похилою асимптотою, якщо границя відношення функції до її аргументу дорівнює числу k при аргументі, що прямує до нескінченності і якщо границя різниці функції і kx дорівнює числу b при аргументі, що прямує до нескінченності.

Границя функції двох змінних

Означення. Число А називається границею функції z=f(x;y) при , , якщо для будь-якого існує число таке, що при виконанні нерівності виконується нерівність і позначається або .

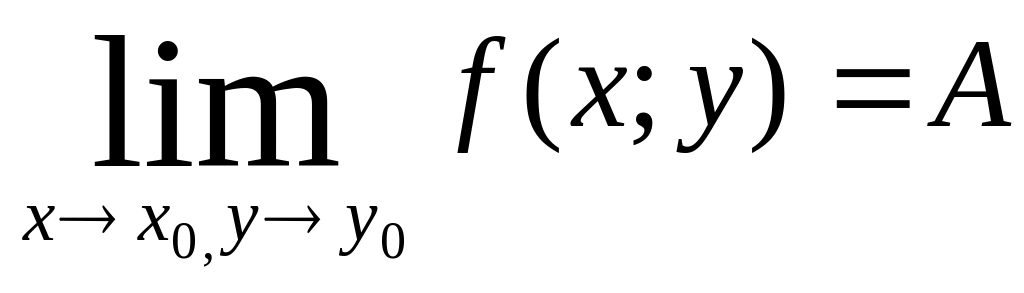Зауваження. Для функції багатьох змінних справедливі теореми про границю суми, добутку та частки, які аналогічні відповідним теоремам для функції однієї незалежної змінної.

Наведемо формулювання відповідних теорем.

Теорема 1. Якщо функція z=f(x;y) має границю при (x;y) (x₀;y₀) , то вона єдина.

Теорема 2. Якщо функція z=f(x;y) має границю при (x;y) (x₀;y₀) , то вона обмежена в деякому околі точки (x₀;y₀) .

Теорема 3. Якщо , 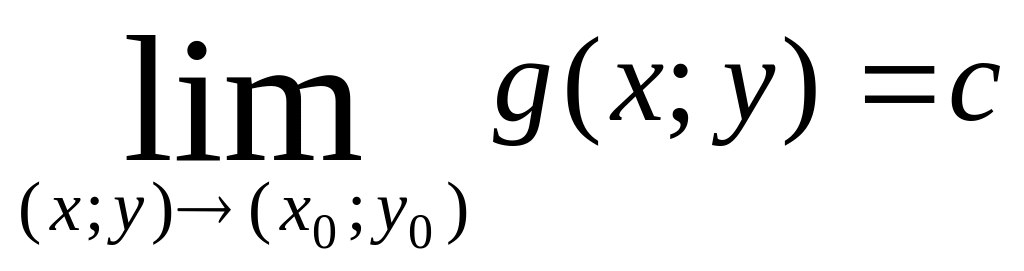і в деякому околі точки (x₀;y₀) виконується нерівність f(x;y) g(x;y), то b .

Теорема 4. Нехай , . Тоді:

1) ;

2) ;

3) 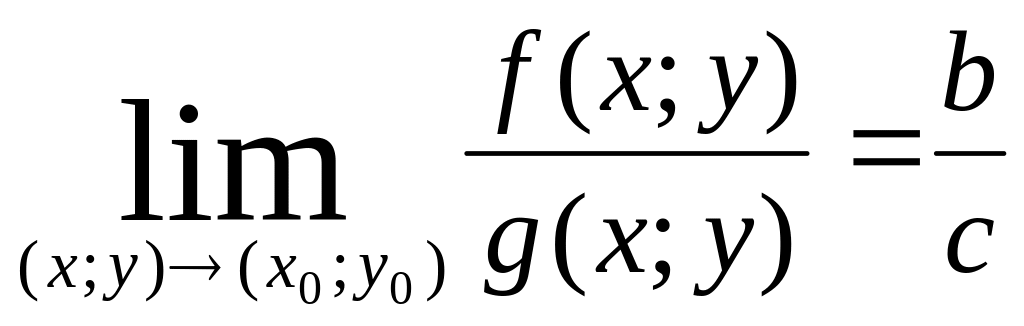(с .

Список ілюстрацій

• Рисунок 1

• Рисунок 2

• Рисунок 3

• Рисунок 4

• Error: Reference source not found

15