4.3 Влияние случайных ошибок измерений на точность определяемого по двум лп места.

4.3.1 Смещение и вес лп.

Ошибки в измерениях навигационного параметра к ошибкам в изолиниях, а значит, и в ЛП, которые их заменяют. Навигационные параметры по которым строятся изолинии и ЛП, могут получаться совершенно разными способами и иметь величины ошибок имеющих разные размерности и величины, учитывая это для унификации удобно применять среднеквадратическое смещение ЛП равное

(4.4)

, где

m_нп – СКП навигационного параметра,

g – его градиент

Она показывает, на сколько линейных единиц смещается ЛП при заданной величине СКП. Величину m_нп называют смещением ЛП или полосой ЛП, т.к. при изменении абсолютного значения U_o, на величину m_нп провести соответствующие этим значениям U'= U_o – m_нп U''= U_o+ m_нп границы, которые определят среднеквадратическую полосу положения. Вероятность попадания истинного значения в эту полосу определяется вероятностью погрешности навигационного параметра, для СКП  0.67, для предельной СКП  0.997, более подробно об этом говорилось ранее.

Весом ЛП называют величину P_i обратно пропорциональную квадрату её смещения, которую рассчитывают по формуле

P_i = 1/ m² _нп

При оценке точности рассматривается вероятность попадания истинного места судна в пределы фигуры ошибок, а не отклонения или ошибки от истинного

места судна. Теоретически необходимо рассматривать вероятность того, что фигура погрешности данной формы и площади данного размера, расположенная в данном месте накроет точку истинного места. Практически рассматривают отклонение, полагая центр фигуры вероятнейшим местом. На практике считают, чтобы погрешности измерения параметров распределены беспрерывно, т.е. мест судна бесконечно много.

Для оценки точности места судна в судовождении применяют: эллипсы и круги погрешностей.

4.3.2 Эллипс погрешностей

При ОМС составляется и решается уравнение, прокладывается изолиния или ЛП отягощенная ошибками измерений. Величины и знаки истинных ошибок измерений носят случайный характер, и учесть их можно лишь статистически.

Вывод формул оценки точности места базируется на предположениях:

1. Грубые ошибки или промахи, пропущенные при измерениях, исключены.

2. Компенсированы систематические ошибки измерений.

3. Ошибки вычислений и графики малы и несущественны.

4. Случайные ошибки измерения подчинены нормальному закону распространения случайных величин.

Рисунок 4.3 – Эллипс погрешностей места судна

Достоинства оценки места судна эллипсом:

1. Он имеет строго теоретическое обоснование.

2. Это единственная кривая, во всех точках которой плотность вероятности ошибки постоянна.

3. Вероятность попадания истинного места судна в область, ограниченную эллипсом, больше, чем у любой другой фигуры одинаковой с эллипсом площади.

4. Эллипс дает рассеяние мест судна по направлениям.

При двух ЛП на практике, достаточно вписать приближенный эллипс в четырёхугольник, образованный полосами погрешностей. При этом вероятнейшим местом судна будет точка пересечения ЛП - центр эллипса погрешностей из-за того, что в элементарно малых окрестностях этой точки вероятность нахождения места судна больше, чем в аналогичных окрестностях любой другой точки.

Для строгого построения эллипса погрешностей рассматриваются векториальные ошибки , линии положения 1 и 2 по направлению ЛП₂ и ЛП₁.

Учитывая, что вектора - сопряжённые полуоси эллипса используют теорему Аполлония

(4.5)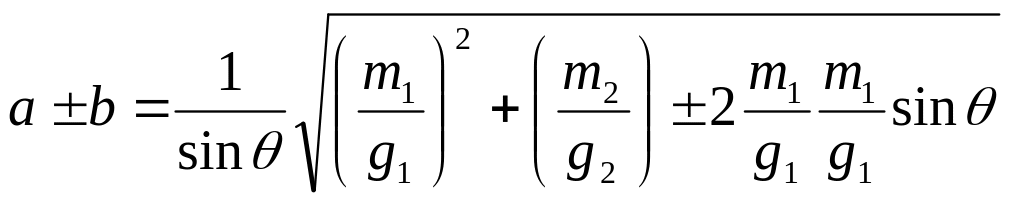

или

(4.6)

;

Где  угол, определяющий направление большой полуоси эллипса, который всегда откладывается внутри острого угла  от более точной ЛП.

Ещё один способ расчета эллипса погрешностей по 2-м ЛП, заключается в использовании таблицы прил. № 5 к МТ-75 Аргументами для входа в таблицу служат величины

и

(4.7)

угол. Из таблицы выбирают К_а, К_b и Полуоси рассчитывают по формуле:

Таблица приложений S составлена по преобразованным формулам Аполлония.

(4.8 )

;