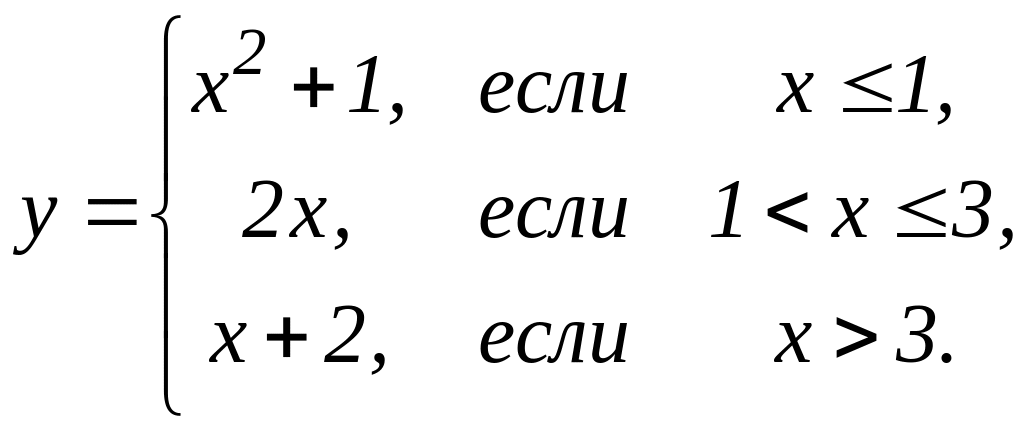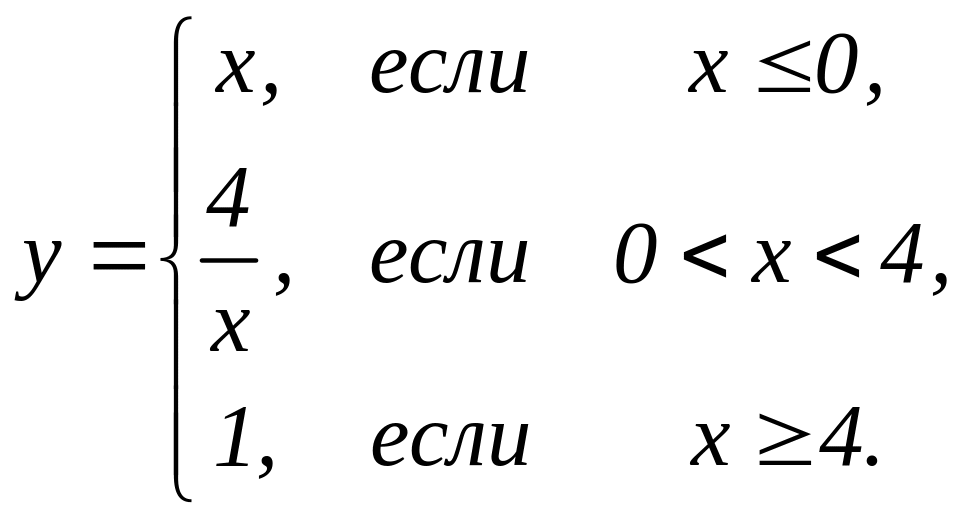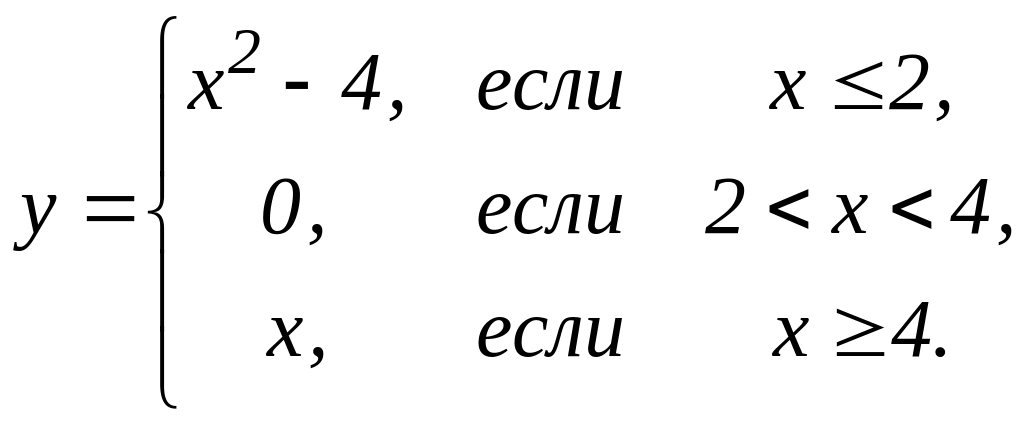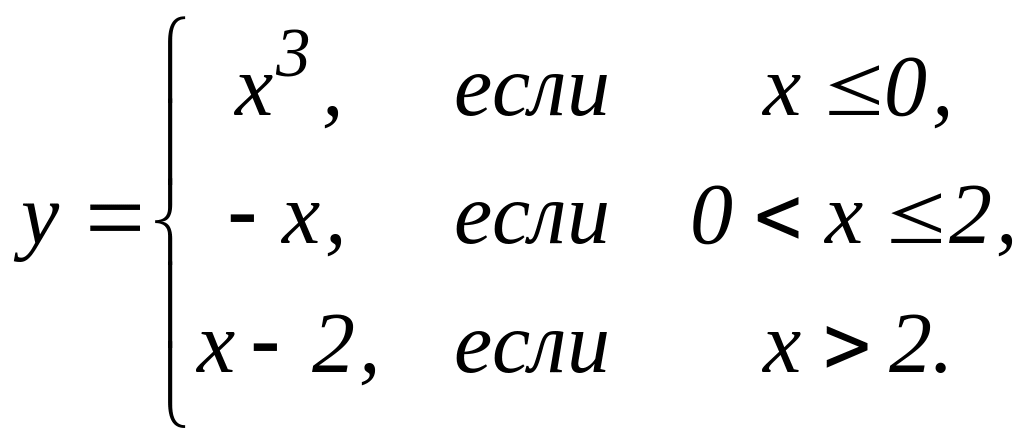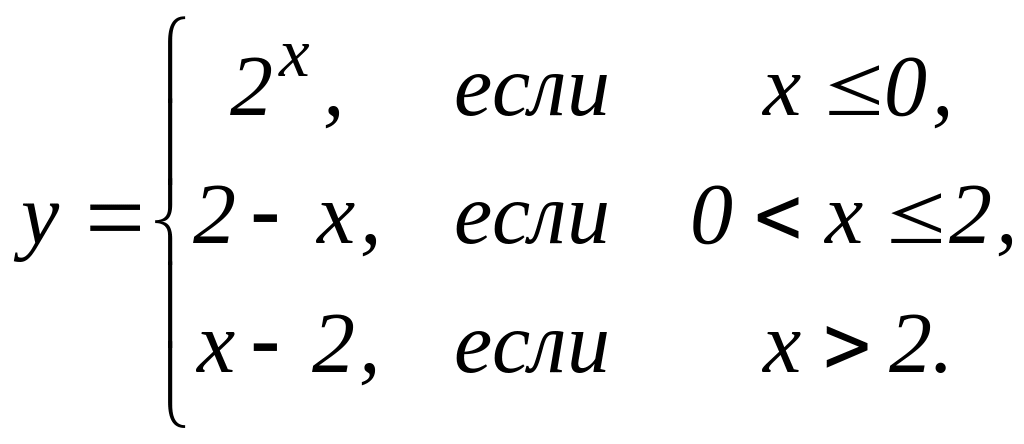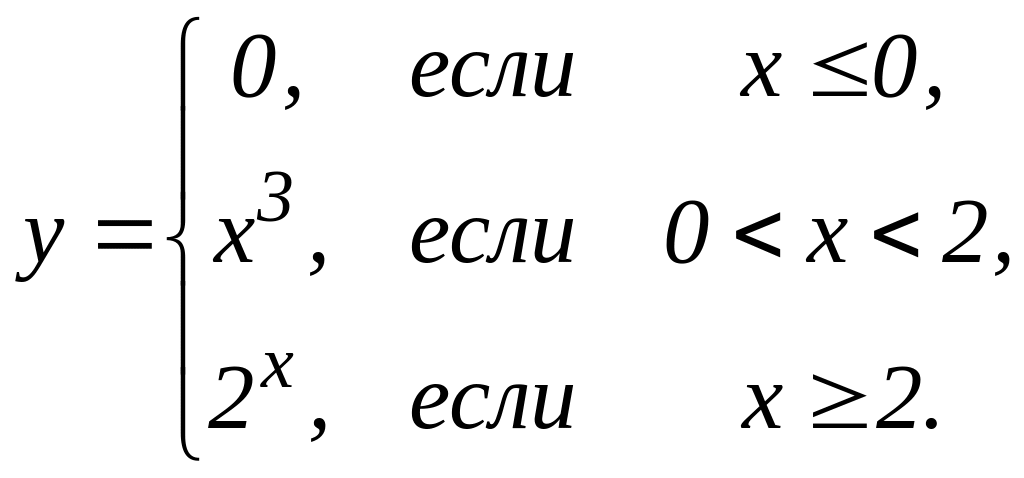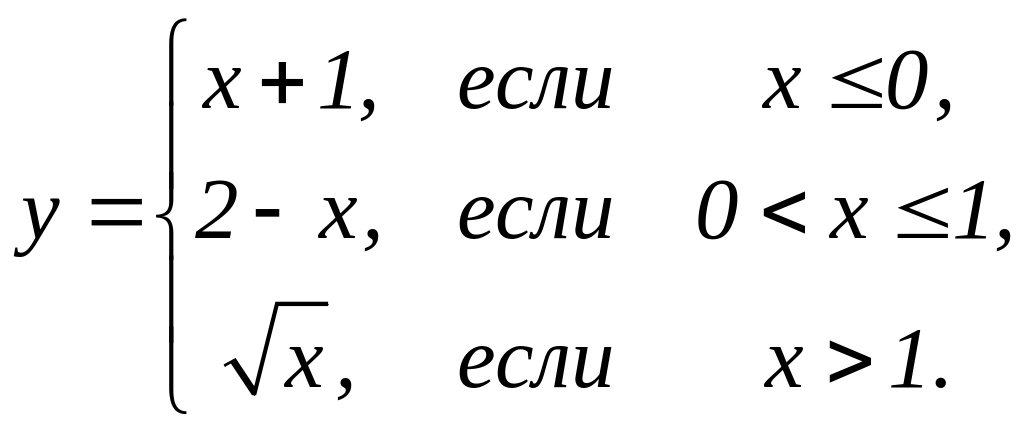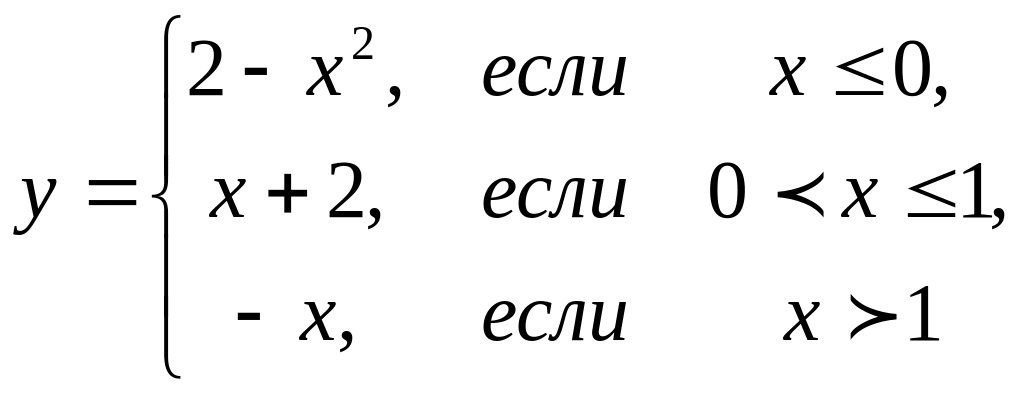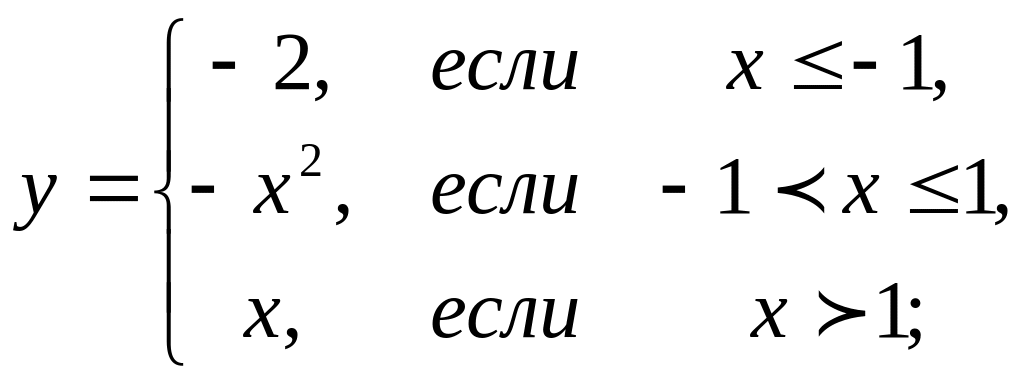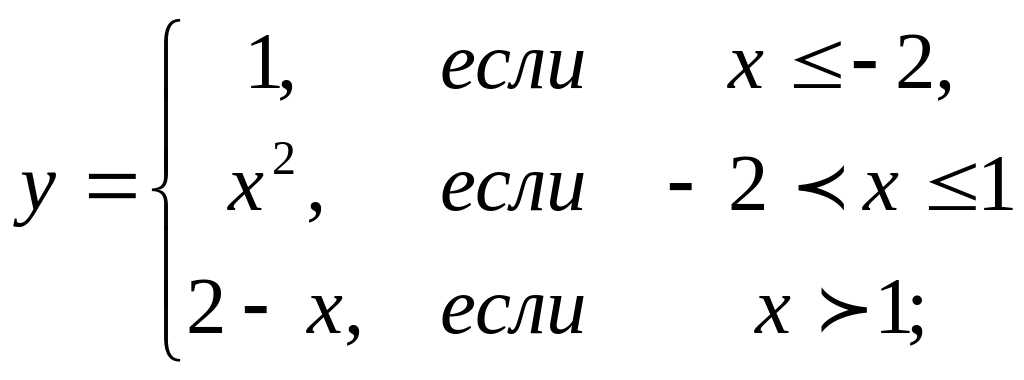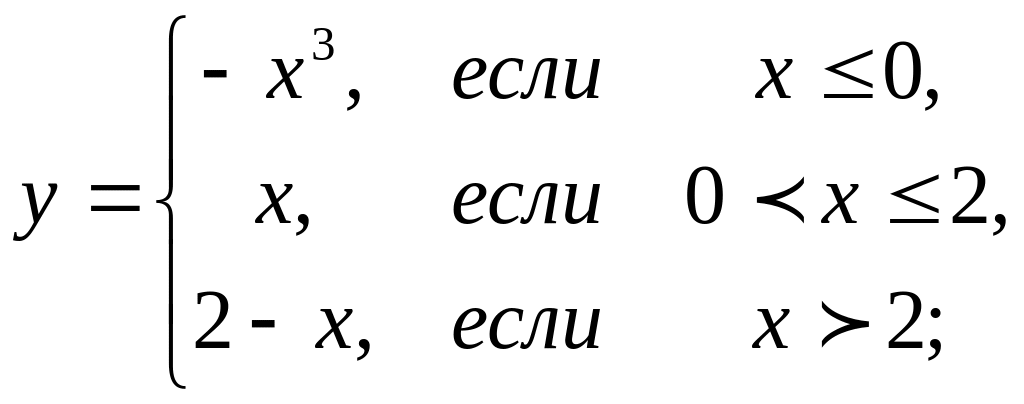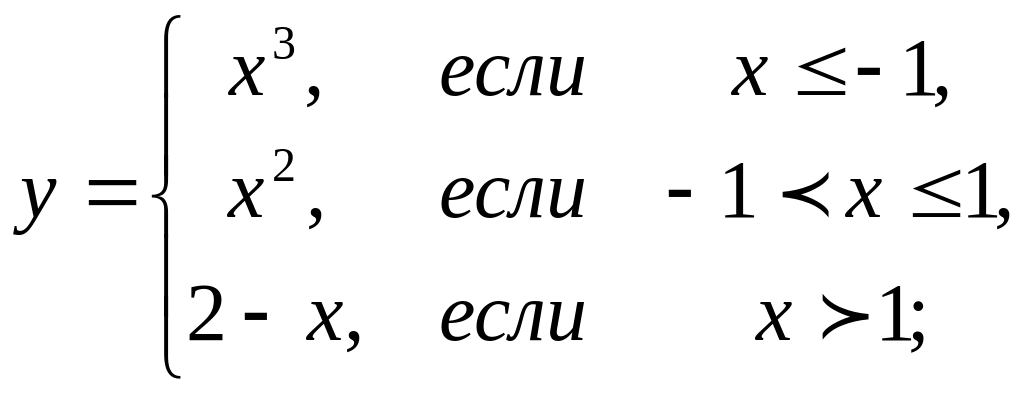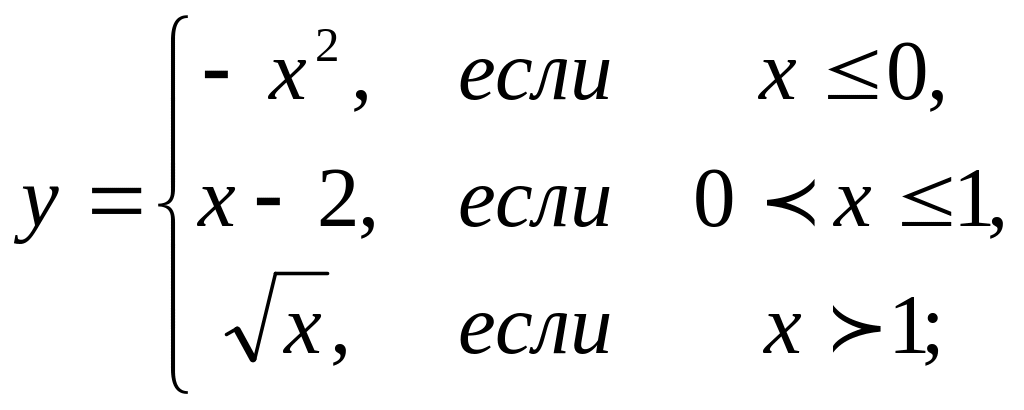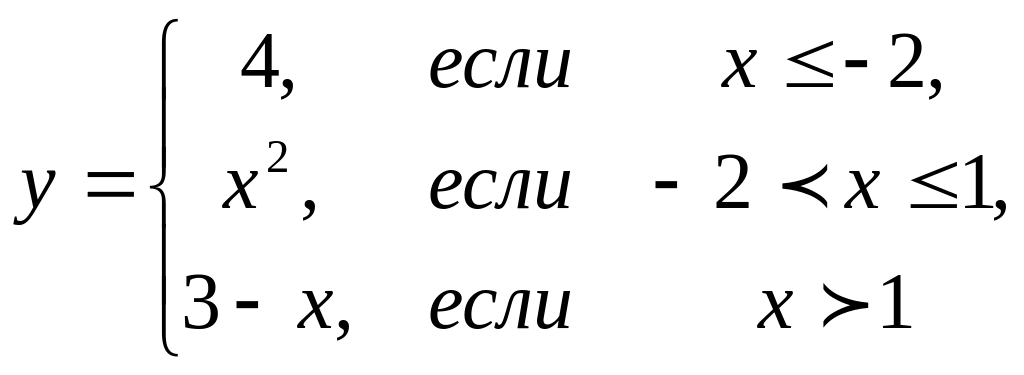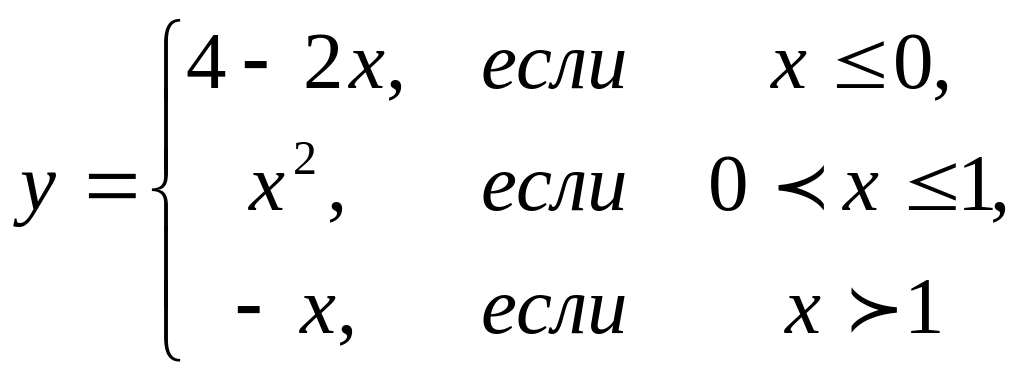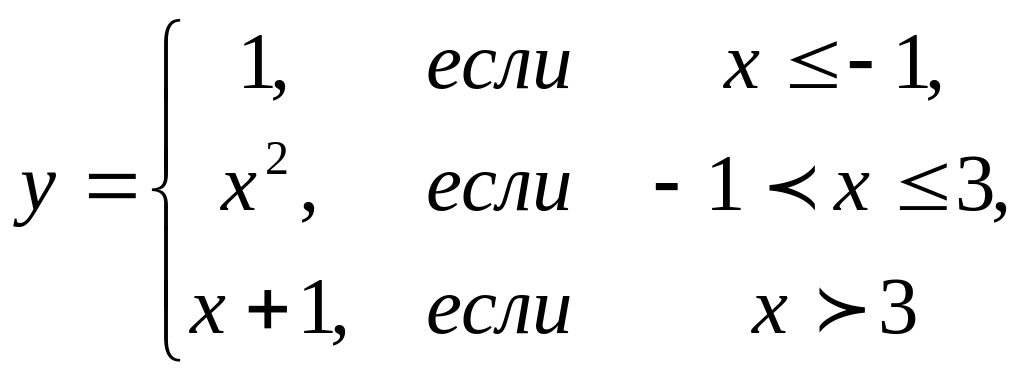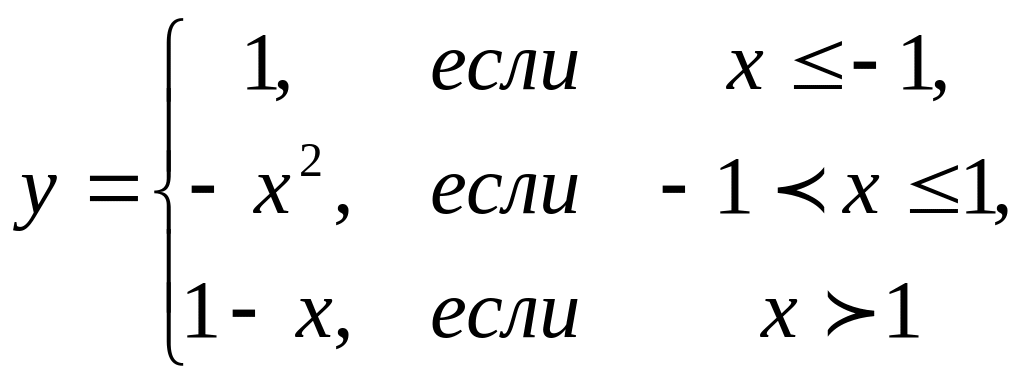- •191028, С.-Петербург, ул. Моховая, 26
- •На титульном листе должны быть указаны:
- •Раздел 1 Линейная алгебра и аналитическая геометрия
- •Раздел 2 Введение в математический анализ
- •Раздел 3 Основы дифференциального и интегрального исчисления
- •Раздел 4 Обыкновенные дифференциальные уравнения
- •Раздел 5 Вероятность и элементы математической статистики
- •Л итература
- •Контрольная работа № 1 Задания
- •1. Дана система уравнений. Решить её методом последовательных исключений.
- •2. Даны координаты точек а, в, с, d. Найти:
- •3. Даны координаты вершин треугольника а, в, с. Найти уравнения сторон ав и ас и угол между ними. Сделать чертеж
- •4. Предел функции и непрерывность. Найти точки разрыва функции, если они существуют. Сделать чертеж функции
- •5 . Найти производные указанных функций
- •6. Вычислить предел функций, используя правило Лопиталя
- •Найти интервалы монотонности и экстремумы функции.
- •Контрольная работа № 2
- •1. Найти площадь фигуры, ограниченной областью d:
- •2. Дифференциальные уравнения первого порядка
- •3. Непосредственный подсчет вероятности. Теоремы сложения и умножения вероятности
- •4. Испытания по схеме Бернулли
- •5. Дискретные случайные величины
- •6. Непрерывные случайные величины
- •7. Найти по заданному вариационному ряду выборки выборочное среднее , выборочную дисперсию . Построить полигон относительных частот
3. Даны координаты вершин треугольника а, в, с. Найти уравнения сторон ав и ас и угол между ними. Сделать чертеж
№ |
А |
В |
С |
№ |
А |
В |
С |
3.1 |
(-5, 3) |
(10,6) |
(1, 5) |
3.11 |
(14, 5) |
(4, 5) |
(-5,-8) |
3.2 |
(-7, 1) |
(5, 0) |
(2, 5) |
3.12 |
(10, 2) |
(2, 0) |
(5, -2) |
3.3 |
(5, 1) |
(0, 3) |
(-2, 4) |
3.13 |
(0, -2) |
(-2, 1) |
(3, 1) |
3.4 |
(5, 2) |
(-1, 0) |
(4, 4) |
3.14 |
(-1, 2) |
(1, -1) |
(-5, 1) |
3.5 |
(2, -2) |
(3, -4) |
(2, -1) |
3.15 |
(4, 8) |
(-3, 3) |
(7, 5) |
3.6 |
(1, 0) |
(2, 5) |
(-1,1) |
3.16 |
(4, 4) |
(5, 2) |
(-1, 0) |
3.7 |
(0, -3) |
(1, 4) |
(-2,-1) |
3.17 |
(-2, 4) |
(5, 1) |
(0, 3) |
3.8 |
(-2, 1) |
(3, 1) |
(0, -2) |
3.18 |
(2, 5) |
(-1,1) |
(1, 0) |
3.9 |
(-3, 3) |
(7, 5) |
(4, 8) |
3.19 |
(1, 5) |
(-5, 3) |
(10,6) |
3.10 |
(2, 0) |
(5, -2) |
(10, 2) |
3.20 |
(1,4) |
(-2,-1) |
(0, -3) |
Решение типового примера
Даны координаты вершин треугольника АВС: А(1, 2), В(3, 5), С(2, 3). Найти уравнения сторон АВ и АС и угол между ними.
Решение:
Определим стороны АВ и АС треугольника АВС:

Рис. 1. Треугольник АВС
![]() ,
то есть
,
то есть
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
.
Таким образом, угловые коэффициенты прямых соответственно равны
![]()
откуда получаем значение тангенса угла А
 ,
,
а угол определяем по таблицам или с помощью калькулятора:
![]() .
.
4. Предел функции и непрерывность. Найти точки разрыва функции, если они существуют. Сделать чертеж функции
4.1 |
|
4.2 |
|
4.3 |
|
4.4 |
|
4.5 |
|
4.6 |
|
4.7 |
|
4.8 |
|
4.9 |
|
4.10 |
|
4.11 |
|
4.12 |
|
4.13 |
|
4.14 |
|
4.15 |
|
4.16 |
|
4.17 |
|
4.18 |
|
4.19 |
|
4.20 |
|
Решение типового примера
Найти
точки разрыва функции
 если
если

На
интервалах
![]() ,
,
![]() и
и
![]() функция непрерывна, так как представляет
собой элементарные функции. Проверке
подлежат только точки x
= -2 и x
= 0.
функция непрерывна, так как представляет
собой элементарные функции. Проверке
подлежат только точки x
= -2 и x
= 0.
Рассмотрим точку x = -2.
Вычислим односторонние пределы
![]() ,
,
 .
.
Так как односторонние пределы не совпадают, но конечны, x=-2 – это точка разрыва функции 1-го рода.
Рассмотрим точку x=0:
 ,
,
![]() .
.
X = 0 - точка непрерывности функции, так как в ней выполнено условие непрерывности (предел справа равен пределу слева).

Рис. 2. Точка разрыва первого рода