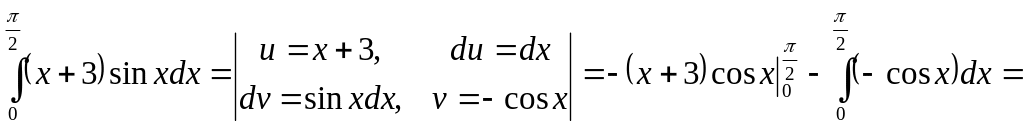Контрольная работа 4
1. Найти неопределенные интегралы (в заданиях а), б), в) правильность результатов проверить дифференцированием).

Проверим полученный результат дифференцированием:
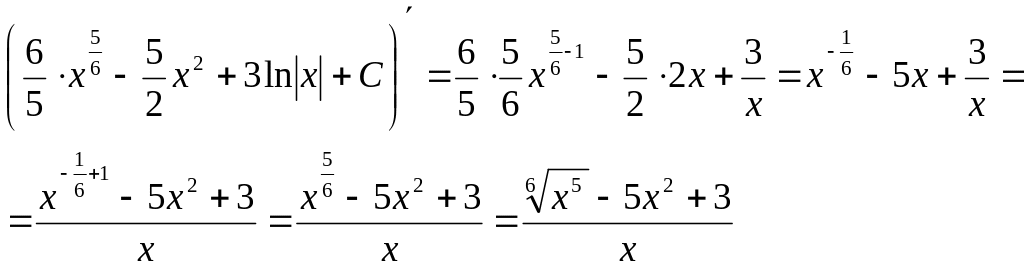
Поскольку в результате дифференцирования получили подынтегральную функцию, то интеграл найден верно.
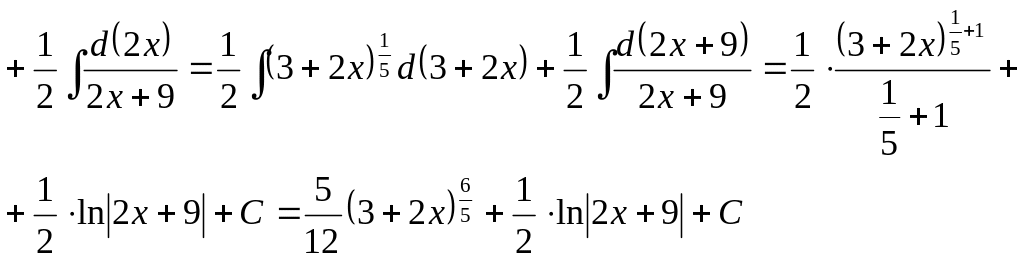
Проверим полученный результат дифференцированием:
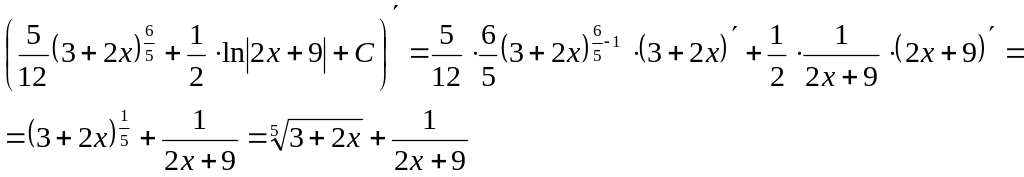
Поскольку в результате дифференцирования получили подынтегральную функцию, то интеграл найден верно.
![]()
Проверим полученный результат дифференцированием:

Поскольку в результате дифференцирования получили подынтегральную функцию, то интеграл найден верно.
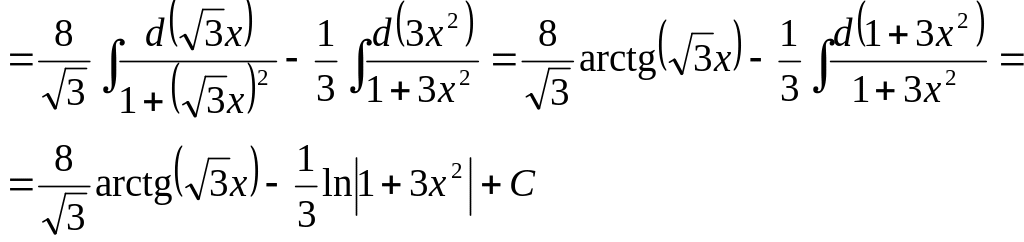

Разложим подынтегральную дробь на сумму простейших дробей:

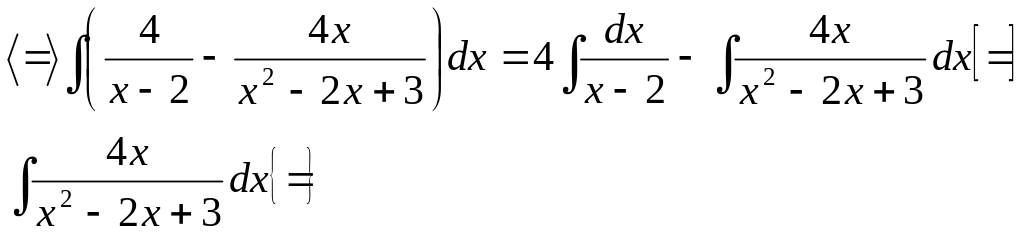
Выделим полный квадрат в знаменателе:
![]()
Сделаем
замену
![]() ,
,
![]() ,
тогда
,
тогда
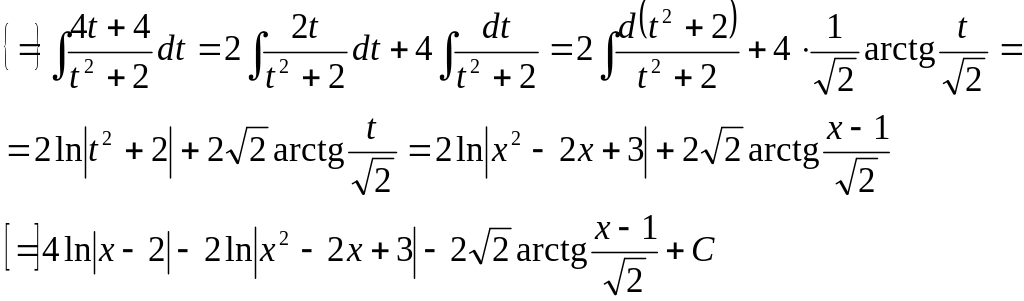
12. Вычислить определенные интегралы
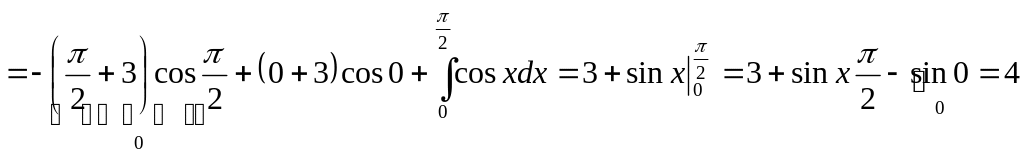
![]()
21. Вычислить интеграл с помощью формулы Симпсона, разбив интервал интегрирования на 10 частей.
![]()
Решение:
Вычислим
шаг интегрирования:
![]()
Для решения задачи заполним таблицу:
|
|
|
|
|
0 |
0,60 |
0,7625 |
|
|
1 |
0,69 |
|
0,7157 |
|
2 |
0,78 |
|
|
0,6716 |
3 |
0,87 |
|
0,6307 |
|
4 |
0,96 |
|
|
0,5931 |
5 |
1,05 |
|
0,5586 |
|
6 |
1,14 |
|
|
0,5271 |
7 |
1,23 |
|
0,4984 |
|
8 |
1,32 |
|
|
0,4722 |
9 |
1,41 |
|
0,4483 |
|
10 |
1,50 |
0,4264 |
|
|
Сумма |
|
1,1889 |
2,8517 |
2,2640 |
Тогда искомое значение интеграла определим следующим образом:
![]()
32. Вычислить
площадь плоской фигуры, ограниченной
заданными линиями:
![]() ,
,
![]() ,
,
![]() .
.
Решение:
Построим заданные линии и определим фигуру, площадь которой требуется найти:

Тогда искомую площадь определим следующим образом:
![]()
![]() (кв.
ед.)
(кв.
ед.)
КОНТРОЛЬНАЯ РАБОТА 5
1. Найти общее решение (общий интеграл) дифференциального уравнения.
– дифференциальное уравнение с разделяющимися переменными
разделим переменные в данном уравнении:

Проинтегрируем обе части полученного уравнения с разделенными переменными:
![]()
![]() – общий
интеграл дифференциального уравнения
– общий
интеграл дифференциального уравнения
![]()
![]() – уравнение
в однородных функциях.
– уравнение
в однородных функциях.
Сделаем
замену:
![]() ,
тогда
,
тогда
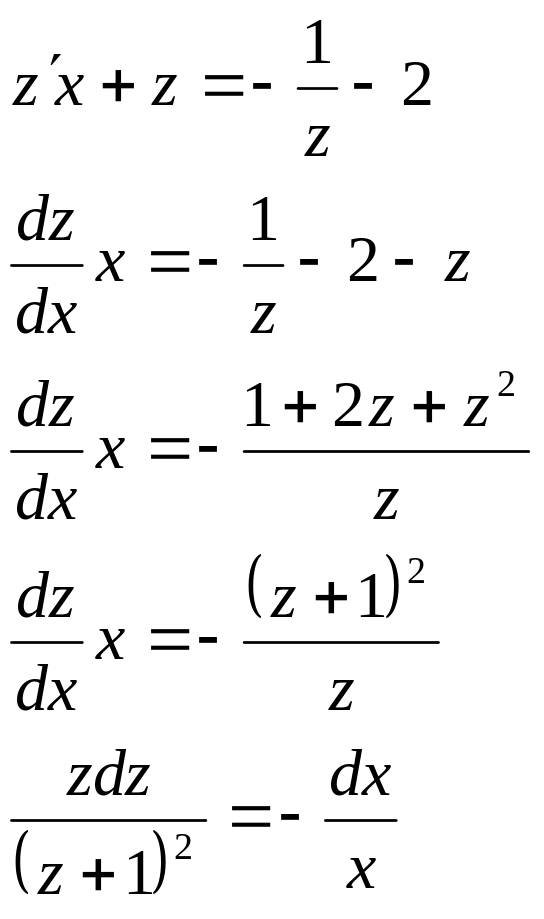
Проинтегрируем обе части полученного уравнения с разделенными переменными:

![]() – общий
интеграл дифференциального урвнения
– общий
интеграл дифференциального урвнения
12. Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
![]() ,
,
![]() ,
,
![]()
Решение:
Сделаем
замену
![]() ,
тогда
,
тогда
![]() – неоднородное
дифференциальное уравнение первого
порядка.
– неоднородное
дифференциальное уравнение первого
порядка.
Решим
его методом Бернулли. Пусть
![]() ,
тогда
,
тогда
![]()
Подберем
функции
![]() и
и
![]() так, чтобы
так, чтобы
![]() (*)
(*)
Решим первое уравнение системы (*):

Проинтегрируем обе части полученного уравнения с разделенными переменными:
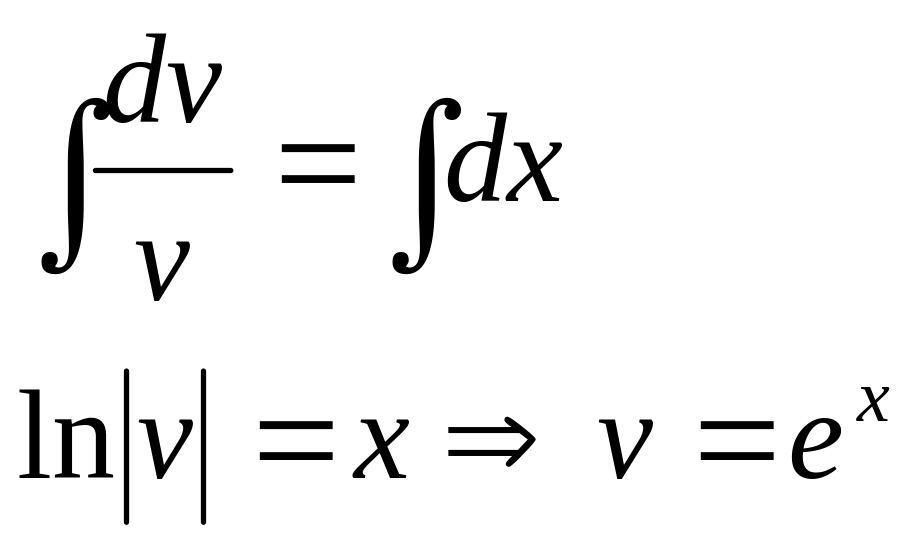
Подставим полученное выражение для функции во второе уравнение системы (*):

Согласно
начальным условиям,
![]() или
или
![]()
Тогда
![]() .
Решим данное уравнение:
.
Решим данное уравнение:
![]() .
.
Согласно
начальным условиям,
![]() или
или
![]() .
.
Окончательно
получим:
![]() .
.
21. Исследовать положительный числовой ряд на сходимость
![]()
Решение:
Для исследования ряда на сходимость проверим выполнение необходимого признака сходимости знакоположительных рядов:

Поскольку необходимый признак не выполнен, то ряд расходится
32. Найти область сходимости степенного ряда
![]() (1)
(1)
Решение:
Найдем радиус сходимости данного ряда:
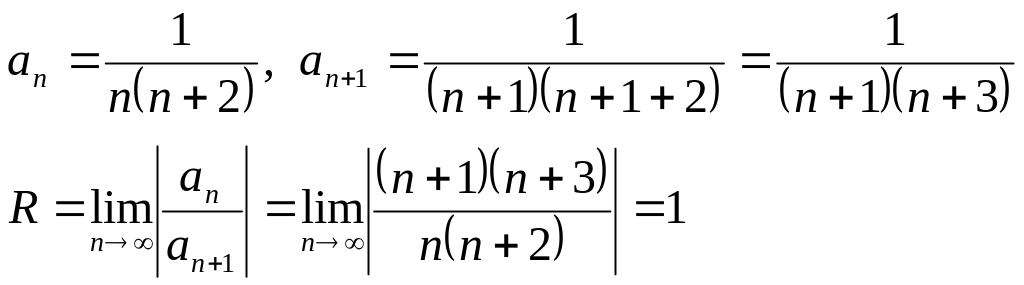
Таким
образом, ряд (1) сходится при
![]() .
.
Исследуем сходимость ряда на концах интервала.
:
![]() (2)
(2)
Для
исследования ряда (2) на сходимость
применим предельный признак сравнения
и сравним его со сходящимся рядом
![]() (3):
(3):
![]()
Поскольку
![]() или
или
![]() ,
то ряды (2) и (3) ведут себя одинаково, т.е.
ряд (2) сходится.
,
то ряды (2) и (3) ведут себя одинаково, т.е.
ряд (2) сходится.
:
![]() (4)
(4)
Для исследования ряда (4) на сходимость проверим выполнение требований признака Лейбница:
 требования
признака Лейбница выполнены, ряд (4)
сходится.
требования
признака Лейбница выполнены, ряд (4)
сходится.
Рассмотрим
ряд из модулей:
![]() .
Данный ряд является сходящимся (см.
ряд(2)). Поскольку ряд (4) и ряд из модулей
сходятся, то ряд (4) сходится абсолютно.
.
Данный ряд является сходящимся (см.
ряд(2)). Поскольку ряд (4) и ряд из модулей
сходятся, то ряд (4) сходится абсолютно.
Таким
образом, окончательно получаем: ряд (1)
сходится при
![]() ,
причем, при
соответствующий знакочередующийся ряд
сходится абсолютно.
,
причем, при
соответствующий знакочередующийся ряд
сходится абсолютно.
41. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд и почленно интегрируя этот ряд.

Решение:
Воспользуемся
известным разложением
![]()
Полагая
![]() ,
получим:
,
получим:
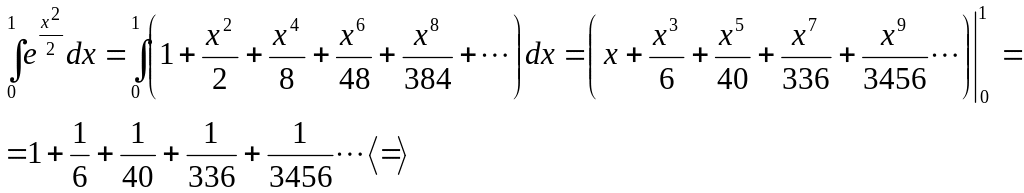
Поскольку
![]() ,
а
,
а
![]() ,
то с точностью до 0,001 получим:
,
то с точностью до 0,001 получим:
![]() .
.
КОНТРОЛЬНАЯ РАБОТА 6
1. Дана
функция
![]() .
Показать, что
.
Показать, что
![]()
Решение:
Вычислим
частную производную
![]() ,
считая при этом
,
считая при этом
![]() постоянной величиной:
постоянной величиной:
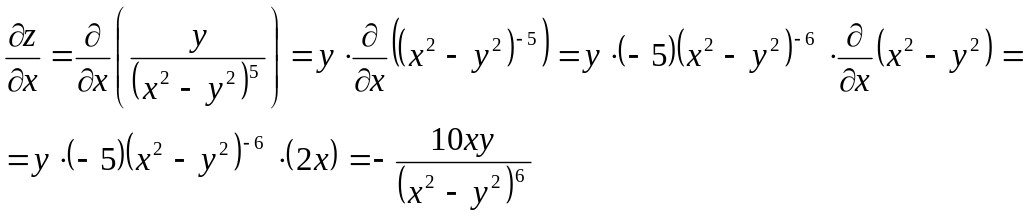
Вычислим
частную производную
![]() ,
считая при этом
постоянной величиной:
,
считая при этом
постоянной величиной:
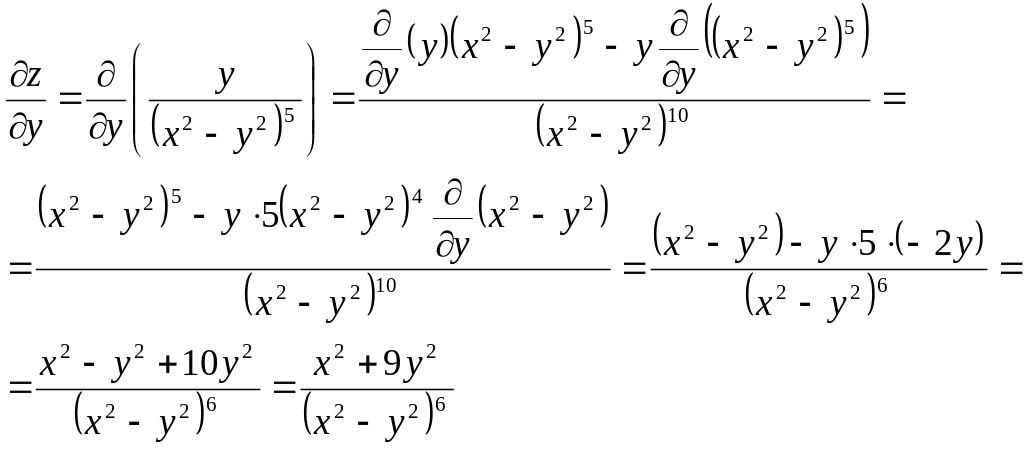
Подставим найденные производные в указанное уравнение:

12. Дана
функция
![]() и две точки
и две точки
![]() и
и
![]() .
Требуется:
.
Требуется:
вычислить значение
 функции в точке
;
функции в точке
;вычислить приближенное значение
 функции в точке
,
исходя из значения
функции в точке
,
исходя из значения
 функции в точке
,
заменив приращение функции при переходе
от точки
к точке
дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции
дифференциалом;
функции в точке
,
заменив приращение функции при переходе
от точки
к точке
дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции
дифференциалом;составить уравнение касательной плоскости к поверхности в точке
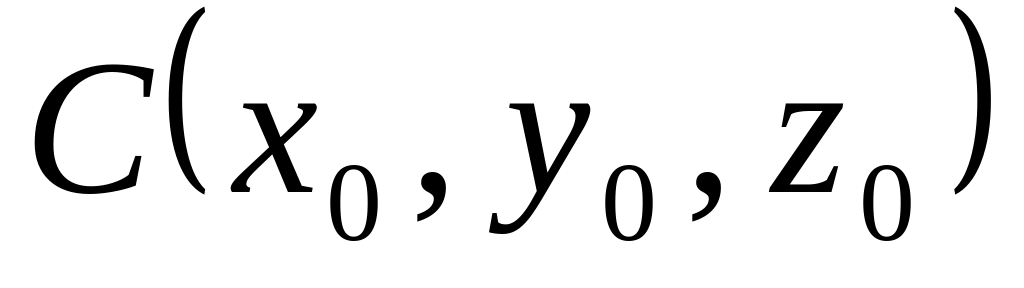 и проверить, лежит ли точка
и проверить, лежит ли точка
 в этой плоскости.
в этой плоскости.
![]() ,
,
![]() ,
,
![]()
Решение:
![]() ,
,
![]()
![]() ,
,
![]() ;
; ![]() ,
,
![]()
Тогда
![]()
Относительная
погрешность
![]()
Составим уравнение касательной плоскости в точке
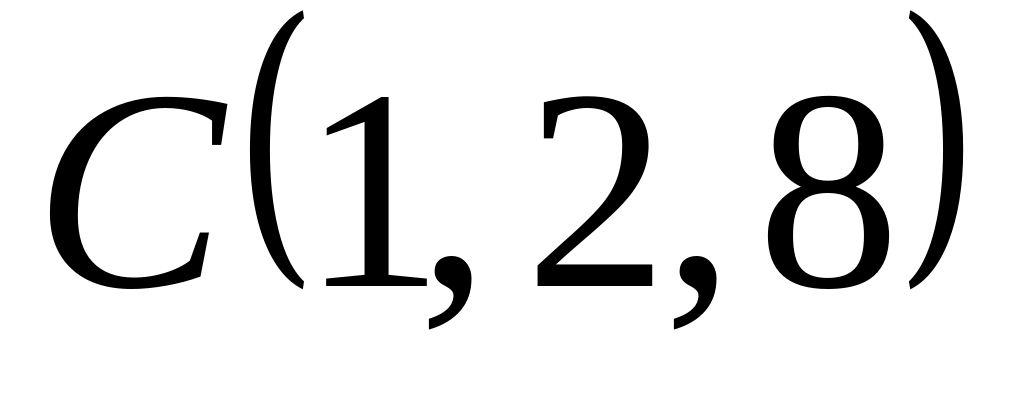 :
:
![]()
![]() – искомое
уравнение касательной плоскости
– искомое
уравнение касательной плоскости
Проверим,
лежит ли в этой плоскости точка
![]() :
:
![]() ,
следовательно, данная точка на принадлежит
касательной плоскости.
,
следовательно, данная точка на принадлежит
касательной плоскости.
21. Найти
наименьшее и наибольшее значения функции
![]() в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми
![]() ,
,
,
,
![]() .
.
Решение:
Построим заданную область:

Найдем экстремумы функции. Для этого воспользуемся необходимым условием экстремума:
![]()
Вычислим частные производные данной функции:
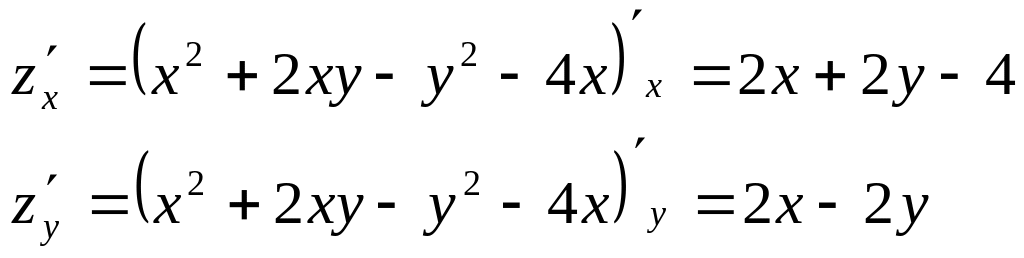
Тогда
![]()
Проверим,
наблюдается ли экстремум в точке
![]() .
Для этого вычислим частные производные
второго порядка:
.
Для этого вычислим частные производные
второго порядка:
![]()
Составим и вычислим определитель:
![]()
Поскольку
![]() ,
то в точке
экстремума нет, поэтому из дальнейшего
рассмотрения ее можно исключить.
,
то в точке
экстремума нет, поэтому из дальнейшего
рассмотрения ее можно исключить.
Рассмотрим границу области.
На
отрезке
:
![]() ,
,
![]() ,
поэтому функция принимает вид:
,
поэтому функция принимает вид:
![]() .
.
Вычислим
производную данной функции:
![]() .
Приравниваем найденную производную к
нулю и находим критические точки:
.
Приравниваем найденную производную к
нулю и находим критические точки:
![]() .
.
Нашли
критическую точку
![]() .
.
На
отрезке
:
![]() ,
,
![]() ,
поэтому функция принимает вид:
,
поэтому функция принимает вид:
![]() .
.
Вычислим
производную данной функции:
![]() .
Приравниваем найденную производную к
нулю и находим критические точки:
.
Приравниваем найденную производную к
нулю и находим критические точки:
![]() .
.
Нашли
критическую точку
![]() .
.
На
отрезке
![]() :
,
:
,
![]() ,
поэтому функция принимает вид:
,
поэтому функция принимает вид:
![]() .
.
Вычислим
производную данной функции:
![]() .
Приравниваем найденную производную к
нулю и находим критические точки:
.
Приравниваем найденную производную к
нулю и находим критические точки:
![]() ,
тогда
,
тогда
![]()
Нашли
критическую точку
![]() .
.
Вычислим значения функции в найденных критических точках и в угловых точках области:

Из найденных значений выбираем наименьшее и наибольшее:
![]() ,
,
![]() .
.
32. Даны:
функция
![]() ,
точка
и вектор
,
точка
и вектор
![]() .
Требуется найти:
.
Требуется найти:
 в
точке
;
в
точке
;производную в точке по направлению вектора .
![]() ,
,
![]() ,
,
![]()
Решение:
Найдем частные производные функции
 :
:

Вычислим значения производных в точке :
![]()
Тогда
![]()
Найдем направляющие косинусы вектора :

Найдем производную в точке по направлению вектора :
![]()
41. Вычислить
двойной интеграл по области
![]() ,
ограниченной указанными линиями.
,
ограниченной указанными линиями.
![]() ,
,
![]()
Решение:
Построим заданную область и определим пределы интегрирования:

Тогда
![]()