Блочный принцип моделирования производственных систем

Независимо от структуры математического описания, в общем случае, стремятся строить сложную модель из элементарных моделей, применяя ранее составленные программные блоки (модули), допускающие их использование в различных моделях. Это способствует экономии средств и времени, затрачиваемых на разработку модели.

При моделировании производственных систем программные модули также могут быть чрезвычайно полезными. Например, модель функционирования сталеплавильного цеха, независимо от того, является он конвертерным, мартеновским или электросталеплавильным, должна включать в свой состав вспомогательные модели таких участков, как шихтовый двор, разливочный пролет, миксер, цех подготовки составов и др.

При моделировании технологического процесса блоками могут быть отдельные уравнения или системы уравнений, являющиеся моделями элементарных процессов. В случае моделирования производственной системы программными модулями служат модели производственных участков, которые, в свою очередь могут включать в себя такие стандартные блоки, как датчики: детерминированных функций, распределенных по различным законам; вычисления средних значений, дисперсий и других характерных распределений.

При блочном моделировании возникает задача стыковки элементарных моделей, которая включает в себя несколько аспектов.

Первый аспект стыковки моделей носит чисто вычислительный характер. Рассмотрим случай, когда элементарными моделями являются алгебраические уравнения. Например, дана следующая система уравнений:

4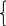 x + y = 33;

x + 3y = 22.

Решать ее будем методом последовательных приближений. Для этого построим итерационный² контур счета. Выберем какое-нибудь значение для y (например, y = 29), подставим его в первое уравнение и получим, что x = 1. Это значение подставим во второе уравнение и получим, что y = 7. Новое значение подставим в первое уравнение и найдем из него x и т.д.

Вычисления внесены в таблицу 1.1. Уже на четвертом шаге мы получили решение системы x = 7; y = 5.

Таблица 1.1

Решение системы уравнений методом последовательных приближений при правильном построении итерационного контура счета

Уравнение	Переменные	Шаг
		1	2	3	4
4x = 33	y	29	7	5,2	5
	x	1	6,5	7	7
4x = 22	x	1	6,5	7	-
	y	7	5,2	5	-

Это оказалось возможным благодаря правильному построению итерационного контура, что обеспечило так называемую устойчивость решения. Если бы итерационный контур был построен другим образом, то мы не получили бы устойчивого решения. Зададим, например, x = 6 и из первого уравнения найдем, что y = 9. Подставим это значение во второе уравнение и установим, что x = - 5. Снова обратимся к первому уравнению и т.д. Вычисления показывают, что мы не приближаемся, а удаляемся от него.

Это явление называют дивергенцией решения. При счете на ЭВМ оно приводит к аварийной остановке вычислительной машины.

Чтобы избежать дивергенции решения в данном примере нужно уравнения решать относительно тех переменных, которые входят в уравнения с наибольшими коэффициентами (первое – относительно x, второе – относительно y).

Другим аспектом проблемы стыковки моделей является конструктивный. Стыковка блоков должна быть конструктивно оформлена таким образом, чтобы модель могла функционировать.

Вернемся к системе:

4 x + y = 33;

x + 3y = 22.

Для того чтобы первый блок (4x + y = 33) мог функционировать, нужно знать y, а для того чтобы второй блок работал, должно быть известно x. Получается порочный круг: для нахождения y нужно знать x, а для нахождения x нужно знать y. Выход из этой ситуации состоит в том, что в модели должен быть еще какой-то блок, который введет в первое уравнение начальное значение y.

Таким образом, обязательным элементом модели должен являться специальный блок, который управлял бы ее работой. Основная задача этого блока состоит в согласовании функций отдельных блоков модели. В данном конкретном примере оказалось достаточным введение начальных условий в первый блок. В общем же случае управляющий блок представляет собой механизм, который осуществляет развитие процесса в модели согласно упорядоченной последовательности вычислений и логических операций. Управляющий блок согласует все операции, происходящие в модели. Каждой такой операции соответствует единственный логический путь функционирования блоков. По окончании этой операции управление моделью снова передается управляющему блоку. Так продолжается до окончания процесса моделирования. Часто роль управляющего блока может играть логическая связь событий, которые происходят случайным или заранее определенным образом.

Наряду с двумя рассмотренными аспектами проблемы стыковки моделей существует еще одна трудность, обусловленная моделированием сложных систем, когда невозможно разместить объединенную модель в вычислительной машине. Тогда процесс моделирования осуществляют по частям, прибегая к так называемой статической стыковке моделей.

Пример, рассмотренный выше, относится к динамической стыковке. При такой стыковке блоки модели функционируют как единое целое, точно так же, как в реальной системе. Выходные параметры одних блоков без предварительной обработки подаются на вход других. При статической стыковке информация о работе каждого блока не только собирается в некотором накопителе, но и статистически обрабатывается там. Сущность обработки сводится к построению различных условных распределений. В этом случае внешняя информация, необходимая для работы какого-либо блока, поступает из накопителя в результате процедуры перебора значений соответствующей случайной величины.

Конечно, лучшим видом стыковки является динамическая. Однако при больших размерах объединенной модели статическая стыковка может оказаться очень полезной, поскольку она позволяет моделировать отдельно работу каждого блока.