Аналіз частотних характеристик кіл

В курсовій роботі в якості прикладу аналізу частотних характеристик кіл розглядаються коефіцієнти передачі по напрузі.

Послідовність аналізу може бути такою:

1. записується вираз операторного коефіцієнта передачі кола по напрузі;

2. Оператор p замінюється на ;

3. Шляхом перетворень вираз для комплексного коефіцієнту передачі K(jω) приводиться до вигляду:

тобто записується в показниковій формі. Тут модуль K(jω) представляє амплітудно-частотну характеристику кола (АЧХ), а аргумент θ(ω) фазочастотну характеристику кола (ФЧХ).

8

За виразом розраховується та будується графік АЧХ кола, визначається аналітично або графічно смуга пропускання кола, граничні частоти якої відповідають

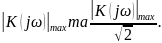
За виразом θ(ω) розраховується та будується ФЧХ кола. Результати розрахунків приводяться в таблицю.

Коефіцієнт передачі К(jω) можна також визначити в загальному вигляді як відношення виразу для комплексної напруги U₂ до напруги U₁.

Енергія сигналу

В загальному випадку енергія визначається як інтеграл від миттєвої потужності Р(t):

де S(t) – напруга, тобто

В теорії сигналів R = 1 Ом, тоді

9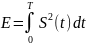

Розкладання періодичної несинусоїдної функції в тригонометричний ряд Фур’є

Відомо, що періодичну функцію, яка задовольняє умовам Дирихле, можна розкласти в ряд Фур’є:

де А₀ - постійна складова;

A_0m, ω₁ = 2π/τ, ψ₁ - амплітуда, кутова частота та початкова фаза першої гармоніки; k-порядковий номер гармоніки.

Ряд Фур’є можна записати і іншій формі, а саме:

9

Перехід до 1-ої форми ряду Фур’є здійснюється за формулами:

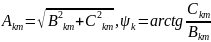
10

Розв’язок завдання 1

	Дано:
Рис.1. Схема електричного кола для розрахунку перехідного процесу класичним методом

11

а) класичний метод

1. Визначаємо НПУ:

2. Визначаємо

3. Визначаємо корені характеристичного рівняння:

4. Отримаємо:

5. 

11

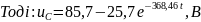
6. Визначимо

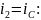
7. Знайдемо :

8. Визначаємо :

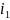9. Протабулюємо та побудуємо графік для шуканої величини:

Таблиця 1. Значення струму

t	0
	2.106	1.677	1.52	1.442

10. Будуємо графік перехідного струму

12

Рис. 2. Графік перехідного струму

б) операторний метод

	НПУ : Примітка: ми поміняли паралельні вітки для спрощення обчислень, тому систему рівнянь контурних струмів розв’яжемо лише для
Рис.3.Схема електричного кола для розрахунку перехідного процесу операторним методом

1. Складаємо систему рівнянь (для контурних струмів):

3. Розв’яжемо методом Крамера:

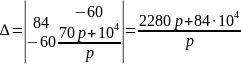
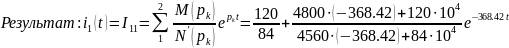
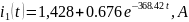
Відповіді обох методів ідентичні, отже розв’язок вірний.

13
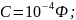