7.6. Идентификация порядка разности модели

На практике для выявления значений параметров p и q АРПСС модели используются автокорреляционные и частные автокорреляционные функции.

Шаг 1. Воспользуемся радом первых разностей (рисунок 7.2) и в окне Transformations of Variables (Преобразование переменной) выберем вкладку Autocorrs (Автокорреляция).

Шаг 2. Для построения автокорреляционной функции необходимо выбрать кнопку Autocorrelations (Автокорреляция), при этом можно регулировать уровень значимости, указывая соответствующее значение в окне p-level for highlighting. В результате проведения процедуры получаем график представленный на рисунке 7.6.

Для расчета частной автокорреляционной функции выберем кнопку Partial autocorrelations, результаты представим на рисунке 7.7.

Рисунок 7.5 – Окно выбора расчета автокорреляционной, частной автокорреляционной функции и кросскорреляции (приведена часть исходного окна)

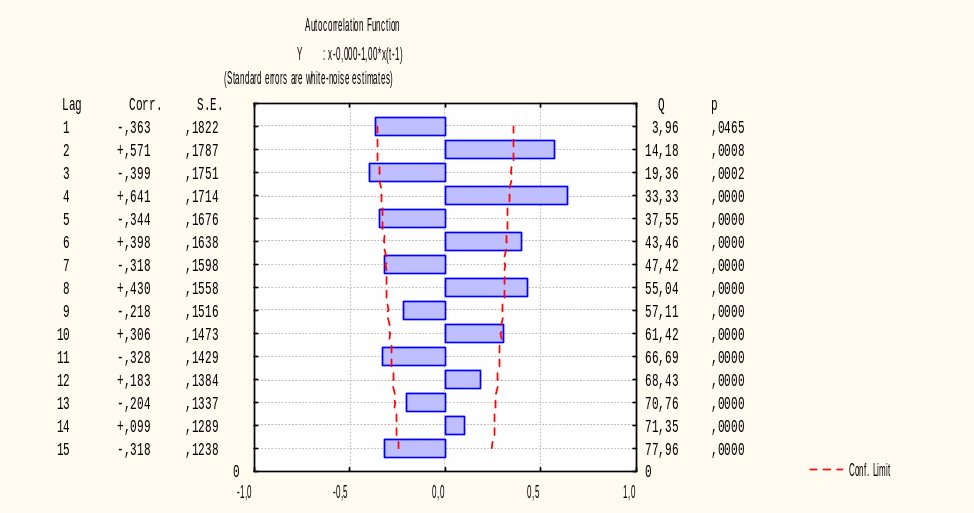
Рисунок 7.6 – Автокорреляционная функция

Рисунок 7.7 – Частная автокорреляционная функция

Обратимся к таблице 7.1 и попытаемся идентифицировать ARMA модель. Поведение автокорреляционной функции (экспоненциально затухает) согласуется с моделью ARMA (1,0) или ARMA (2,0). При этом поведение частной автокорреляционной функции (согласно рисунку 7.7, имеем выбросы на втором и четвертом лаге) не согласуется с данными моделями. Поэтому необходимо рассчитаем вторые разности, для этого во вкладке x=f(x) выбрать Autocorr. (x=x-(a+b*x(lag))), в качестве исходной переменной (в верхней части окна) выберем x-0,000-1,00*x(t-1)

Рисунок 7.8– Окно выбора исходной переменной для расчета (приведена часть исходного окна)

В результате получаем следующие автокорреляционные и частные автокорреляционные функции:

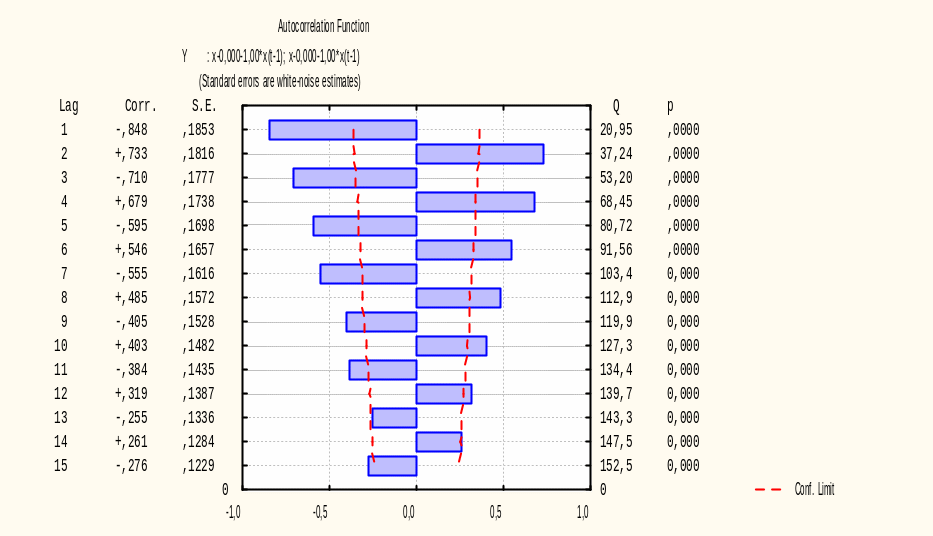
Рисунок 7.9 – Автокорреляционная функция

Рисунок 7.10 – Частная автокорреляционная функция

Полученные данные соответствуют модели ARMA(1,0), так как АКФ - экспоненциально затухает, ЧАКФ - выброс (пик) на лаге 1. После идентификации моделей перейдем к непосредственной оценки ее параметров.

7.7. Построение arma модели

В рассматриваемом пакете программ существует два метода построения авторегрессионных моделей:

1. Построение ARMA модели в модуле Multiple regression

2. Построение ARMA модели в модуле ARIMA & Autocorrelation function

7.7.1. Построение arma модели в модуле Multiple regression

Оценить параметры ARMA модели можно с помощью обычного МНК (но при этом оценки будут смещены). Для реализации этого метода в пакете необходимо:

Шаг 1. Сохранить результаты расчета вторых разностей, для этого в окне Transformations of Variables нажать кнопку Save variables получаем новую таблицу, содержавшую три переменные:

Y – исходный ряд денежного агрегата М0;

Y_1 – ряд первых разностей;

Y_2 – ряд вторых разностей.

Шаг 2. Проведем замену обозначений выведенных переменных: Y_1 засеменим на D’, Y_2 на D’’.

Также необходимо ввести переменную D’’t-1, для этого в главном меню выбираем Insert  Add Variables. В появившемся окне Add Variables в поле Name заменим NewVar на D’’t-1, в поле Long name введем выражение =v3.

Шаг 3. Выбираем в главном меню Date  Shift (Lag) и проводим сдвиг переменной D’’t-1 на один шаг вперед (Forward).

Шаг 4. В главном меню выбираем Statistics  Multiple Regression. В окне Select dependent and independent variable lists (запускается после нажатия кнопки Variables) в качестве зависимой переменной указываем D’’ в качестве не зависимой - D’’t-1.

Шаг 5. Установим галочку возле опции Advanced options (stepwise or ridge regression) в появившемся окне Model Definition в прокрутке Intercept выберем Set to zero (т.е. регрессионное уравнение будет оценено без свободного члена). После оценки получим следующие результаты:

Таблица 7.2 – Результаты оценки модели вида

	Beta	Std.Err. of Betta	B	Std.Err. of B	t(24)	p-level
D''t-1	-0,878	0,098	-0,911	0,101	-8,992	0,000

Согласно результатам построения авторегрессионной модели вида ARMA(1,0), параметр  получен статистически значим. Также необходимо отметить, что модель статистически значима по F-критерию Фишера (F_факт(1,24)=80,86 против F_табл(1,24)= 4,26).

Шаг 6. В окне итогов построения регрессионной модели (Multiple Regression Results) необходимо выбрать вкладку Residuals / assumptions / prediction, далее кнопку .

В появившемся окне Residual Analysis выбираем вкладку Save  Save residuals & predicted, в промежуточном окне Select variables to save with predicted/residual sc… выделим переменную D’’ и нажмем кнопку ОК. Получаем следующую таблицу с результатами:

Рисунок 7.11 – Таблица результат оценки ARMA модели

Шаг 7. На основе полученной таблицы построим график. Выберем в главном меню Graphs  2D Graphs  Line Plots (Variables…). Нажмем кнопку Variables (Переменные) и в появившемся окне укажем переменные D’’ и Predicted. Также в поле Graph type (окно 2D Line Plots –Variables) выделим Multiple (таким образом, на график будет выведены обе переменные одновременно).

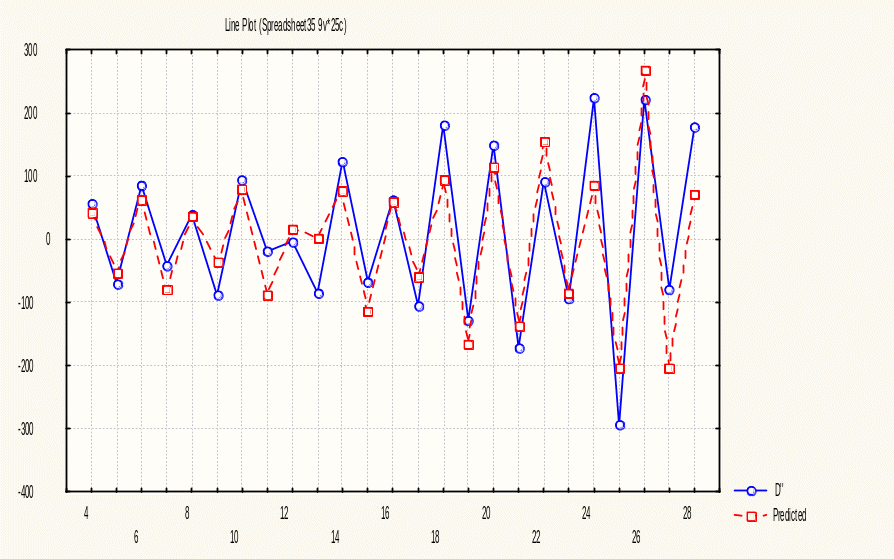
Рисунок 7.12 - Ряд вторых разностей денежного агрегата М0 и модельные данные

Согласно приведенному графику используемая для описания динамики первых разностей авторегрессионная модель ARMA (1,0) очень хорошо описывает анализимруемый ряд.

Шаг 8. Снова обратимся к вкладке Residuals/assumptions/prediction нажмем кнопку Predict dependent variable для прогнозирования уровней исследуемого ряда.

Шаг 9. В окне Specify values for indep. vars укажем последнее значение переменной D’’t-1 равное -79, получим следующий результат:

Таблица 7.3 – Точечный прогноз вторых разностей денежного агрегата М0 на 1 квартал 2006г.

	B-Weight	Value	B-Weight * Value
D''t-1	-0,911	-79,000	71,969
Predicted			71,969
-95,0%CL			55,451
+95,0%CL			88,488

Аналогичным образом рассчитаем значения для 2-4 квартала 2006г. при этом в качестве прогнозного значения будем использовать значение точечного прогноза предыдущего квартала:

Таблица 7.4 - Прогнозные значения вторых разностей денежного агрегата М0 на 2006г.

Квартал/год	Значения показателя для прогноза	Прогноз модели ARMA (1,0)	Нижняя доверительная граница	Верхняя доверительная граница
I/2006	-79,000	71,969	55,451	88,488
II/2006	71,969	-65,564	-80,612	-50,516
III/2006	-65,564	59,729	46,020	73,438
IV/2006	59,729	-54,413	-66,902	-41,924