Примеры для самостоятельного решения

1. Вычислить определители.

1.1. а) б)

1.2. По правилу треугольников:

а) б)

1.3. Разложив по элементам 1-ой строки:

1.4. Разложив по элементам строки (столбца), где больше нулей:

1. Решить системы и сделать проверку.

2.1. По формулам Крамера.

а) б)

2.2. По методу Гаусса.

а) б)

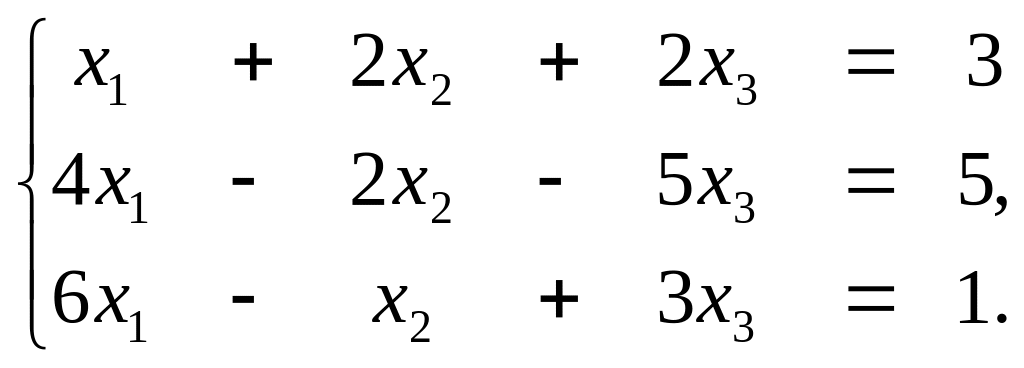
2.3. С помощью обратной матрицы

а) б)

2. Даны точки А(-3, 4, 1), В(2,3,4). Найти разложение вектора по базису векторов , , и длину вектора . Отв.:

3. Даны точки А(0,-2,3), В(2,1,4), С(3,4,5). Найти:

а) координаты (проекции) векторов и

б) координаты вектора

с) длину вектора

4. Даны векторы Найти скалярное произведение векторов .

5. Доказать, что векторы и коллинеарны.

6. Доказать, что векторы ортогональны.

4. Теория пределов и непрерывность

1. Числовая последовательность.

Переменная, пробегающая числовую последовательность

Если каждому натуральному числу n поставлено в соответствие действительное число x_n, т. е.

1, 2, 3, 4, …, n, …

x₁, x₂, x₃, x₄, …, x_n, …

то говорят, что задана числовая последовательность с общим членом x_n. В дальнейшем будем говорить, что задана переменная x, пробегающая числовую последовательность с общим членом x_n. В этом случае эту переменную будем обозначать x_n. Значения переменной x_n изображаются точками на числовой оси.

Например, даны переменные:

: или ;

: 1, 4, 6, …, 2n ..

Число а называется пределом переменной x_n, если для любого сколь угодно малого числа ε > 0 найдется такое натуральное число N, что все значения переменной x_n, у которых номер n больше числа N, удовлетворяют неравенству .

Этот факт символически записывается так:

или

Геометрически это означает, что точки, изображающие значения переменной x_n, сгущаются, накапливаются около точки а.

Отметим, что если переменная имеет предел, то он единственный. Предел постоянной, есть сама постоянная, т.е. , если c=const. Переменная может вовсе не иметь предела.

Например, переменная x_n=(-1)ⁿ не имеет предела, т.е. нет единственного числа, около которого накапливаются значения переменной. Геометрически это очевидно .

2. Ограниченная переменная

Переменная x_n называется ограниченной, если существует такое число M > 0, что |x_n| < M для всех номеров n.

Дана переменная . В качестве числа М можно взять, например, 3. Очевидно, что для всех номеров n. Следовательно, – ограниченная переменная.

Переменная x_n = 2n является неограниченной, т.к. с ростом номера n ее значения увеличиваются и нельзя подобрать такое число M > 0, чтобы |2n| < M для всех номеров n.

Теорема. Если переменная имеет конечный предел, то она ограничена.

Обратная теорема неверна.