Тема 12. Визначений інтеграл.

1. Обчислення визначеного інтеграла

Для неперервної функції на відрізку :

– формула Ньютона Лейбніца

– підінтегральна функція

– підінтегральний вираз

– нижня границя інтегрування

– верхня границя інтегрування

– первісна дія функції

Щоб обчислити визначений інтеграл треба :

1. Знайти первісну для функції ;

2. В отриманий вираз замість змінної спочатку підставити верхню границю інтегрування, а потім нижню границю інтегрування;

3. З першого результату відняти другий результат.

Приклад

2. Основні властивості визначеного інтеграла

1) ;

2) ;

3) ;

4) ;

5) .

3. Геометричний зміст визначеного інтеграла

Криволінійною трапецією називають фігуру, обмеженої графіком функції , прямими і віссю абсцис.

Геометричний зміст визначеного інтеграла полягає у тому , що визначений інтеграл дорівнює площі криволінійної трапеції.

Площа криволінійної трапеції обчислюється за формулою:

Я

кщо площі тоді для знаходження можна скористатися формулою:

Якщо фігура обмежена графіками неперервних функції таких, що для будь-якого , де абсциси точок перетину, тоді для знаходження її площі можна скористатися формулою

4. Фізичний зміст інтеграла

Під час прямолінійного руху переміщення чисельно дорівнює де швидкість руху

5. Обчислення об’ємів тіл

Нехай криволінійна трапеція опирається на відрізок осі абсцис та обмежена зверху графіком функції , невід’ємної та неперервної на відрізку .

Унаслідок обертання цієї криволінійної трапеції навколо осі абсцис утворюється тіло , об'єм якого можна знайти за формулою:

Приклад 1. Обчислити за допомогою формули Ньютона Лейбніца інтеграли.

Приклад 2.

Обчислити площу фігури, обмеженої лініями

Розв’язання

На координатній площині зображаємо задані лінії. Графіком функції є парабола, вітки якої направлені вгору.

s

0

Відповідь: 9( кв. од.)

Приклад 3.

Обчислити площу фігури, обмеженої лініями та віссю

Розв’язання

1. На координатній площині зображаємо задані лінії . Графіком функції є парабола, вітки якої направлені вгору.

2. Знайдемо координати вершини параболи:

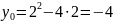
3. Знайдемо абсциси точок перетину параболи

Отже, числа 0 та 4 – границі інтегрування.

На відрізку функція від’ємна. Знайдемо площу фігури.

Відповідь: (кв. од.)

П

риклад 4.

О

бчислити площу фігури, обмеженої лініями

Р

озв’язання

Н

а координатній площині зображаємо задані лінії:

1. Г

   рафіком є парабола, вітки якої направлені в гору. Знайдемо координати вершини параболи.

Отже (0;2) – координати вершини

2. Знайдемо абсциси точок перетину параболи з прямою

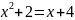
Отже, числа 1 та 2 – границі інтегрування.

3. Графіком є пряма, що проходить через точки

	0	-1	2
	4	3	6

Відповідь: (кв. од.)