§ 12. Циркуляция и ротор электростатического поля

В § 6 мы выяснили, что силы, действующие на заряд q в электро­статическом поле, являются консервативными. Следовательно, ра­бота этих сил на любом замкнутом пути Г равна нулю:

Сократив на q, получим соотношение

(12.1)

Рис. 12.1.

(ср. с (8.7)).

Интеграл, стоящий в левой части формулы (12.1), представляет собой циркуляцию вектора Е.по контуру Г (см. (11.16)). Таким образом, характерным для электростатического поля является то обстоятельство, что циркуляция вектора напряженности этого по­ля по любому замкнутому контуру равна нулю.

Возьмем произвольную поверхность S, опирающуюся на кон­тур Г. для которого вычисляется циркуляция (рис. 12.1). Согласно теореме Стокса (см. (11.42)) интеграл от ротора Е, взятый по этой поверхности, равен циркуляции вектора по контуру Г:

(12.2)

52 Гл. I. Электрическое поле в вакууме

Поскольку циркуляция равна нулю, мы приходим к выводу, что

Полученное условие должно выполняться для любой поверхности S, опирающейся на произвольный контур Г. Это возможно лишь в том случае, если ротор вектора в каждой точке поля равен нулю:

. (12.3)

По аналогии с крыльчаткой, изображенной на рис. 11.12, пред­ставим себе электрическую «крыльчатку» в виде легкой втулки со спицами, на концах которых помещаются одинаковые по величине положительные заряды q (рис. 12.2; все устройство должно быть малых размеров). В тех местах электрического поля, где ротор Е отличен от нуля, такая крыльчатка вращалась бы с тем большим

Рис. .12.2. Рис. 12.3. Рис. 12.4.

ускорением, чем больше проекция ротора на ось крыльчатки. В случае электростатического поля такое воображаемое устройст­во не пришло бы во вращение при любой ориентации его оси.

Итак, отличительной особенностью электростатического поля является то, что оно безвихревое. В предыдущем параграфе мы выяснили, что ротор градиента скалярной функции равен нулю (см. формулу (11.38)). Поэтому равенство нулю ротора Е в каж­дой точке поля делает возможным представление Е в виде градиен­та скалярной функции , называемой потенциалом. Такое пред­ставление уже было рассмотрено в§8 (см. формулу (8.2); знак ми­нус в этой формуле взят из физических соображений).

Из необходимости соблюдения условия (12.1) можно сразу за­ключить, что существование элекростатического поля вида, пока­занного на рис. 12.3, невозможно. Действительно, для такого поля циркуляция по контуру, изображенному пунктиром, была бы от­лична от нуля, что противоречит условию (12.1). Точно так же невозможно, чтобы поле, отличное от нуля в ограниченном объеме, было во всем этом объеме однородным (рис. 12.4). В этом случае циркуляция по контуру, показанному пунктиром, была бы отлична от нуля.

§ 13. Теорема Гаусса

В предыдущем параграфе мы выяснили, чему равен ротор элек­тростатического поля. Теперь найдем дивергенцию поля. С этой целью рассмотрим поле точечного заряда q и вычислим поток век­тора Е через замкнутую поверхность S, заключающую в себе заряд (рис. 13.1). В § 5 мы показали, что количество линий вектора Е, начинающихся на точечном заряде + q или заканчивающихся на заряде —q, численно равно q/₀.

Согласно формуле (11.10) поток вектора Е через любую замкну­тую поверхность равен числу линий, выходящих наружу, т. е. начинающихся на заряде, если он поло­жителен, и числу линий, входящих внутрь, т. е, оканчивающихся на заряде, если он отрицателен. Учтя, что количе­ство начинающихся или оканчивающихся на точечном заряде линий численно равно q/₀., можно написать,что

,

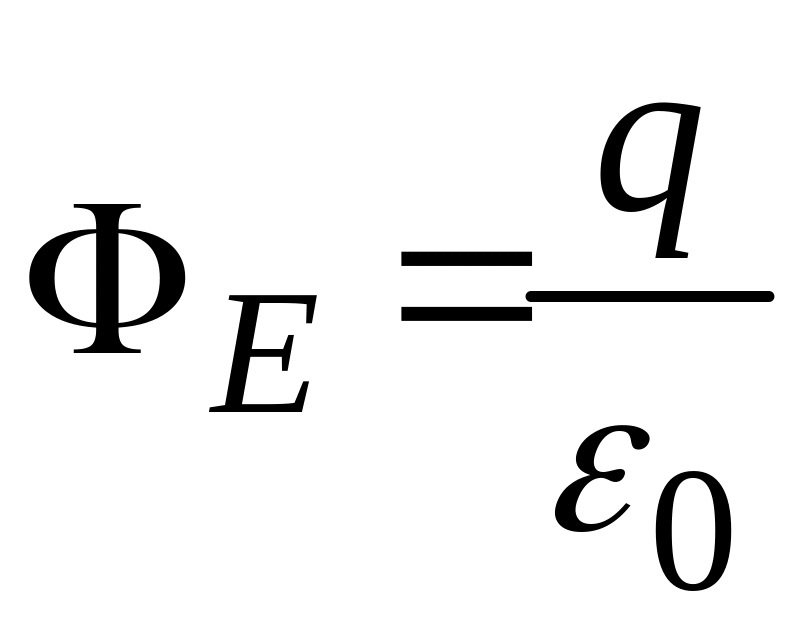(13.1)

З нак потока совпадает со знаком заряда q. Размерность обеих частей равенства (13.1) одинакова. ^Рис' ¹³¹'

Теперь допустим, что внутри замкнутой поверхности находятся

N точечных зарядов q₁, q2…..qn. В силу принципа суперпозиции

напряженность Е поля, создаваемого всеми зарядами, равна сум­ме напряженностей Еi .создаваемых каждым зарядом в отдельно­сти: Поэтому

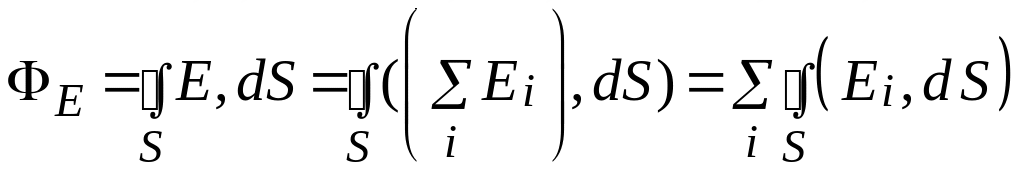
Каждый из интегралов, стоящих под знаком суммы равен qi/₀ EdS = -isV

(13.2)

Доказанное нами утверждение носит название теоремы Гаусса. Эта теорема гласит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраи­ческой сумме заключенных внутри этой поверхности зарядов, де­ленной на .

При рассмотрении полей, создаваемых макроскопическими за­рядами (т. е. зарядами, образованными огромным числом элемен­тарных зарядов), отвлекаются от дискретной (прерывистой) структуры этих зарядов и считают их распределенными в пространстве непрерывным образом с конечной всюду плотностью. Объем­ная плотность заряда р определяется по аналогии с плотностью массы как отношение заряда dq к физически беско­нечно малому объему dV, в котором заключен этот заряд:

В данном случае под физически бесконечно малым объемом нужно понимать такой объем, который, с одной стороны, достаточно мал для того, чтобы плотность в пределах его можно было считать оди­наковой, а с другой стороны, достаточно велик для того, чтобы не могла проявиться дискретность заряда.

Зная плотность заряда в каждой точке пространства, можно найти суммарный заряд, заключенный внутри замкнутой поверхности S. Для этого нужно вычислить интеграл от р по объему, ограниченному поверхностью:

Таким образом, формуле (13.2) можно придать вид

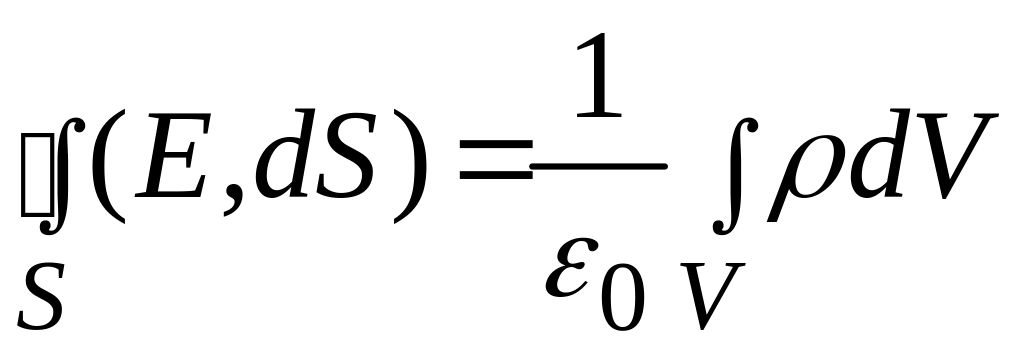(13.4)

Заменив в соответствии с (11.41) поверхностный интеграл объемным, получим

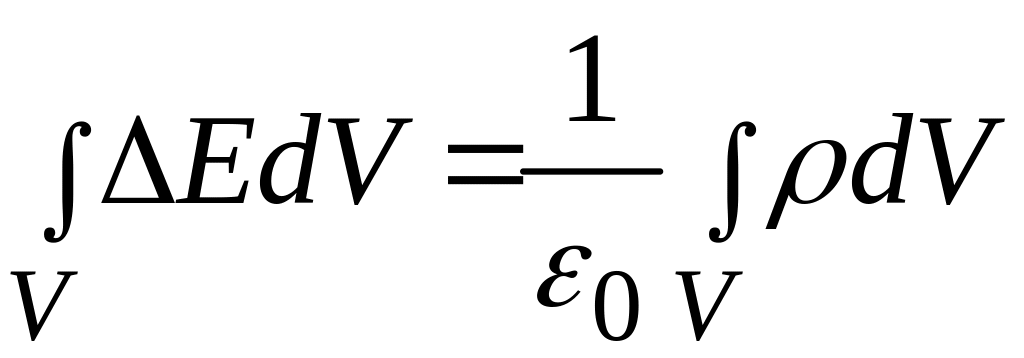
Соотношение, к которому мы пришли, должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора Е связана с плотностью заряда в той же точке равенством

(13.5)

Это равенство выражает теорему Гаусса в дифференциальной форме. В случае текущей жидкости V дает удельную мощность источ­ников жидкости в данной точке. По аналогии говорят, что заряды являются источниками электрического поля.