Лабораторная работа 3 решение систем линейных уравнений

Цель работы: научиться решать системы линейных уравнений различными способами с помощью таблиц EXCEL.

Задание. Решить систему линейных уравнений с использованием таблиц EXCEL

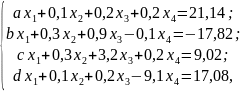
где , , , ,

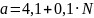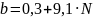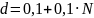N-номер варианта

1. матричным способом;

2. по правилу Крамера.

Пример выполнения лабораторной работы

1) Решим систему линейных уравнений

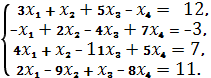
матричным методом.

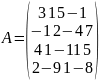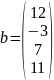
Для решения воспользуемся электронными таблицами EXCEL. Введем элементы матрицы системы уравнений и столбец свободных членов 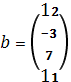в соответствующие ячейки таблицы (рис. 19) и выделим поле ячеек 4×4 для вывода обратной матрицы .

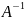Рис. 19.

Далее, воспользуемся командой «Вставить функцию» , выберем функцию вычисления обратной матрицы «МОБР» (рис. 20) и нажмем клавишу «ОК».

Рис. 20

Отметим в качестве массива матрицу (Рис. 21).

Рис. 21

Для вычисления обратной матрицы нажимаем комбинацию клавиш

« Ctrl-Shift-Enter».

Рис. 22

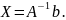
Найдем теперь решение системы Отметим ячейки для вывода решения и воспользуемся встроенной функцией умножения матриц «МУМНОЖ» (рис. 23).

Рис. 23

Нажимая кнопку «ОК» и отмечая соответственно массивы , получим

Рис. 24

Для нахождения решения нажимаем комбинацию клавиш « Ctrl-Shift-Enter».

Рис. 25

2) Решим теперь эту же систему линейных уравнений методом Крамера. Для этого введем матрицу и отметим ячейку (например, В7) для вывода значения определителя Δ матрицы (рис. 26).

Рис. 26

Далее, воспользуемся командой «Вставить функцию» , выберем функцию вычисления определителя «МОПРЕД» (рис. 27) и нажмем клавишу «ОК» (рис. 28).

Рис. 27

Отметим в качестве массива матрицу (рис. 28) и нажмем «ОК».

Рис. 28

В результате найдем определитель Δ (рис. 29).

Рис. 29

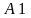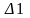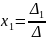
Затем вводим матрицу , полученной из матрицы заменой первого столбца матрицы на столбец свободных членов. Вычислим определитель матрицы и значение неизвестной (рис. 30).

Рис. 30

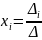
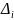
Нажимая клавишу «ENTER», получим, что Аналогичным образом находим остальные неизвестные , где − определитель матрицы, полученной из матрицы путем замены i – го столбца на столбец свободных членов (i=2,3,4) .

Лабораторная работа 4 решение задач линейной алгебры

Цель работы: научить студентов решать задачи линейной алгебры с использованием прикладных математических пакетов MAPLE.

Задания

1. Найти ранг матрицы .

2. Вычислить определитель матрицы B и найти ей обратную. Сделать проверку.

3. Решить систему уравнений двумя способами. Результаты сравнить.

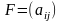4. Предприятие производит 4 вида продукции, используя при этом 4 вида сырья. Для производства одной тонны j – ой продукции расходуется тонн i - го вида сырья . Запасы i - го вида сырья на складе составляют тонн. Определить такой объем выпуска продукции каждого вида, чтобы полностью израсходовать все сырье, имеющееся на складе (нормы расхода задаются матрицей , запасы сырья – вектором ).