
- •Производная функции: определение, геометрический и механический смыслы.
- •Основные правила дифференцирования. Производные основных элементарных функций.
- •3. Производные высших порядков
- •Дифференциал функции. Дифференциалы высших порядков.
- •Дифференциалы высших порядков.
- •Правило Лопиталя и его применение к вычислению пределов.
- •Экстремумы функции
- •8.Первообразная. Неопределенный интеграл
- •9. Основные свойства неопределенного интеграла
- •10. Интегралы от основных элементарных функций.
- •11. Методы интегрирования (метод замены переменой и интегрирование по частям).
- •12. Задачи, приводящие к понятию определенного интеграла (задача о вычислении площади криволинейной трапеции).
- •13.Определенный интеграл: определение, свойства, геометрический смысл.
- •Вопрос 14 Вычисление определенного интеграла: формула Ньютона-Лейбница.
- •15.Приложения определенного интеграла.
- •16.Методы интегрирования в опреленном интеграле.
- •17.Основные понятия теории вероятностей: случайные события - понятие, виды случайных событий; вероятность случайного события. Основные аксиомы теории вероятностей.
- •18. Способы непосредственного вычисления вероятности: классическая, статистическая, геометрическая вероятности.
- •19. Основные элементы комбинаторики: перестановки, размещения, сочетания.
- •20. Операции с событиями: сумма и произведение событий.
- •21. Теорема сложения вероятностей для несовместных событий
- •22. Теорема сложения вероятностей для совместных событий
- •23. Условная вероятность. Теорема умножения вероятностей для зависимых событий
- •Вопрос 24 Условие независимости событий. Теорема умножения вероятностей для независимых событий.
- •26)Формула Байенса(теорема гипотез)
- •27. Формула Бернулли и следствия из нее
- •28. Случайная величина. Дискретные и непрерывные случайные величины
- •29. Закон распределения вероятностей дискретной случайной величины: ряд распределения,
- •30. Биномиальное распределение.
- •31. Распределение Пуассона
- •Вопрос 32 Геометрическое распределение
- •33. Числовые характеристики положения дискретной случайной величины: мода, медиана, математическое ожидание и его свойства.
- •Числовые характеристики рассеивания дискретной случайной величины: дисперсия и ее свойства, среднее квадратическое отклонение.
- •Вопрос 35 Функция распределения случайной величины
- •36.Непрерывная случайная величина и ее законы распределения. Плотность распределения вероятностей, ее свойства.
- •Свойства:
- •37.Закон равномерного распределения вероятностей.
- •Вопрос 38 Показательный закон распределения
- •39. Нормальное распределение
- •Правило 3 сигм:
- •40. Числовые характеристики нсв
8.Первообразная. Неопределенный интеграл
9. Основные свойства неопределенного интеграла

10. Интегралы от основных элементарных функций.
В приведенной ниже таблице основных интегралов u может обозначать
как независимую переменную, так и функцию от независимой переменной
u = φ (x) , т. е. таблица написана с учетом свойства инвариантности (9).
Таблица основных интегралов
Таблица неопределённых интегралов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила интегрирования
|
Если
|
|
|
11. Методы интегрирования (метод замены переменой и интегрирование по частям).
Метод замены переменной
Наиболее общим приемом интегрирования функций является метод
замены переменной (метод подстановки), который применяется тогда, когда
искомый интеграл ∫ f (x)dx не является табличным, но путем ряда преобразо-
ваний он может быть сведен к табличному интегралу.
Способ подстановки основан на применении следующей формулы:

где для перехода от переменной x к переменной t используются формулы:
![]()
Часто употребляется обратная замена переменной, т.е. подстановка
![]()
Интегрирование по частям
Пусть u = u(x) и v = v(x)– две дифференцируемые функции от x .
Дифференциал произведения двух функций uv вычисляется по формуле
d(uv)= udv + vdu .
Интегрируя, получаем uv = ∫udv + ∫vdu , или
∫udv = uv - ∫vdu (13)
Формула (13) называется формулой интегрирования по частям. Этой
формулой пользуются тогда, когда интеграл ∫udv невозможно свести к таб-
личному интегралу с помощью подстановки или труднее найти, чем интеграл
∫ vdu .
Метод интегрирования по частям применяют при вычислении интегра-
лов вида:



12. Задачи, приводящие к понятию определенного интеграла (задача о вычислении площади криволинейной трапеции).
(см. тетрадь)
13.Определенный интеграл: определение, свойства, геометрический смысл.
Определение. Определенным интегралом от функции f (x) на отрез-
ке [a,b] называется конечный предел ее энной интегральной суммы, когда
число элементарных отрезков неограниченно возрастает, а длина наи-
большего из них стремится к нулю.

Из определения следует, что определенный интеграл зависит только
от вида функции f (x) и пределов интегрирования, но не зависит от пере-
менной интегрирования, которую можно обозначить любой буквой, т.е.:

Функция, для которой существует предел (2), называется интегри-
руемой на отрезке [a,b].

Основные свойства определенного интеграла


Это понятно и с геометрической точки зрения: основание криволинейной трапеции имеет длину, равную нулю, следовательно, и площадь ее
рана
нулю.







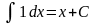





 при
при


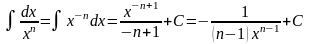






















 ,
то
,
то


