26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга.

Матрица смежности вершин — это квадратная матрица B n-го порядка, элементы которой определяются для неориентированного графа следующим образом:

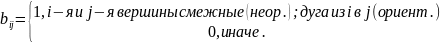
Замечание: в k-ой строке матрицы орграфа количество единиц равно полустепени исхода 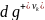вершины 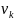, а количество единиц в k-ом столбце — полустепени захода . Для неорграфа матрица смежности вершин симметрична.

Граф (неориентированный и ориентированный) может быть представлен в виде матрицы инциденций размера nm, где n — число вершин, а m — число рёбер (или дуг): 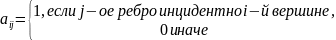(неориентированный граф); 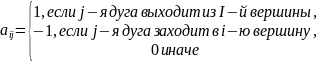(ориентированный граф). Матрица Кирхгофа —

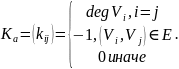
Ранг графа, или циклический ранг, это m-n+k, где n — число вершин, k — число компонент связности, m — число рёбер. Коранг графа, или коциклический ранг, это n-k.

Ранг равен числу фундаментальных циклов, находимому алгоритмом поиска в глубину, т.е. размерности линейного пространства циклов и не зависит от выбора начальной вершины, поскольку все базисы конечномерного линейного пространства состоят из одного и того же числа векторов .

Проверка корректности определения ранга. rkG= rkAc Ac-матрица смежности.

● Пусть G-матрица смежности с заменой элементов главной диагонали на 0. 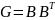,где B-матрица инцндентности. P- матрица перестановки. Положим 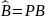– матрица с изм. Нумерацией вершин. Тогда: ; 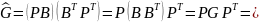G перестановочно подобна. 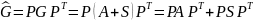, т.е. матрица и диагональ матрицы G меняются по одному закону => .●

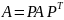27. Деревья. Связь количества вершин и рёбер (неориентированного) де­рева.

Неориентированным деревом называется связный и ациклический граф. Ориентированным деревом называется бесконтурный ориентированный граф, у которого полустепень захода не больше 1и существует только одна вершина (корень ориентированного дерева), полустепень захода которой равна 0.

Теорема. G=(V,E); |V|=n; |E|=m 1. Граф G – дерево 2. Граф G – связан и m=n-1 |E|=|V|-1. 3. Граф G – ацикличен (не содержит цикла) и |E|=|V|-1. 4.  две различные вершины соединяют единственный простой путь в G. 5. G – ацикличен;  V₁, V₂ (не смежные) {V₁V₂}E. Все эти утверждения эквивалентны и могут служить определением дерева.

⊲1.2. Индукция по количеству вершин n=|V| n=1  m=0. G=(V,E) с n вершинами. Рассмотрим — состоит из 2-х связанных компонент, а сам не связан. Т.к. цикла нет, то при исключении e получится не связный граф. 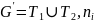— количество вершин в 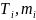— количество рёбер в 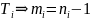(по предположению индукции).

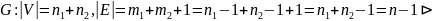
⊲2.3. Пусть G содержит цикл, тогда, выбросив из этого цикла ребро, получим связный граф, где |V|=n, |E|=n-2. Докажем, что такого не бывает.

Лемма: k — количество компонент связанности графа , тогда 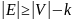. Проведем индукцию по количеству ребер m. m=0 k=|V|00 – верно. Рассмотрим граф с |E|=n. Выбросим из него ребро G\{e}. У него или k, или k+1 компонента связности, а количество рёбер n-1. m-1|V|-k, тогда m|V|-k+1|V|-k; m-1|V|-k-1m|V|-k.⊳ ⊲3.4. G — цикл m=n-1. Предположим, что G состоит из k компонент связности. 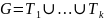— каждая из них дерево. 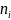— количество вершин — количество рёбер в . ; . 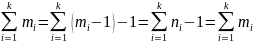Есть хотя бы один путь. И такой путь один, иначе был бы узел⊳