Криволинейный интеграл первого рода

Рассмотрим в плоскости Оху кривую АВ длины l . Пусть - непрерывная в точках дуги АВ функция. Разобьем АВ произвольным образом на n частей с длинами . Выберем на каждой из них произвольным образом по точке M_i , найдем значения функции в этих точках и составим сумму вида (интегральную сумму).

Если существует предел этой суммы при и не зависит от способа разбиения области на элементарные части, от выбора точек M_i , то он называется криволинейным интегралом I рода или по длине дуги.

Вычисление криволинейного интеграла I рода

1. Если линия задана параметрическими уравнениями x=x(t), y=y(t), ( ), то криволинейный интеграл I рода сводится к определенному интегралу по формуле

.

2. Если линия задана уравнением y=y(x), , то справедлива формула

.

Замечание.

Анализируя определения двойного, тройного, криволинейных интегралов, замечаем общность их конструкции. Сделаем общую схему их определения

1. Выбираем точку
2. Составляем произведение
3. Составляем интегральную сумму
4. Переходим к пределу при

Приложения криволинейных интегралов

1. Длина дуги кривой .

2. Масса материальной кривой с - линейной плоскостью

.

3. Работа силы при перемещении материальной точки вдоль дуги кривой L:

.

4. Площадь фигуры, лежащей в плоскости Оху и ограниченной замкнутой линией L:

или или ,

где - интеграл по замкнутому контуру L.

5. Координаты центра тяжести дуги с линейной плотностью

; .

Пример 11.

Вычислить криволинейный интеграл , где L – отрезок прямой, заключенный между точками А(0,-4) и В(2,0)

Решение

Уравнение прямой, соединяющей точки А и В :

, , ,

Так как кривая L задана уравнением, то криволинейный интеграл I рода, взятый по этой кривой, сводится к определенному интегралу по формуле

Найдем .

Значит

.

Пример 12.

Вычислить криволинейный интеграл ,

где L – первая арка циклоиды x=a(t-sint)

y=a(1-cost) .

Решение

Так как кривая задана параметрическими уравнениями, то криволинейный интеграл в этом случае сводим к определенному интегралу по формуле

Вычисляя дифференциалы

, ,

находим дифференциал дуги

.

Тогда

.

Пример 13.

Вычислить криволинейный интеграл взятый вдоль пространственной кривой L - части винтовой линии

x=4cost, y=4sint, z=3t .

Решение

В этом случае криволинейный интеграл сводится к определенному по формуле

.

Вычисляя дифференциалы

; ; .

получаем дифференциал дуги

.

Тогда

.

Пример 14.

При помощи криволинейного интеграла найти длину дуги кривой

, между точками пересечения ее с осями координат.

Решение

Для этого воспользуемся формулой .

Найдем точки пресечения кривой с осями координат:

Таким образом, t изменяется от 0 до

Пример 15.

Пользуясь криволинейным интегралом, найти площадь, ограниченную кривой

Решение

Воспользуемся формулой для вычисления площади фигуры, расположенной в плоскости хОу и ограниченной замкнутой линией L:

Данная кривая

- это эллипс с полуосями a=2, b=3.

Переходя к параметрическим уравнениям эллипса

x=2cost, y=3sint, ,

преобразуем криволинейный интеграл к определенному так:

.

Пример 16.

Найти массу дуги кривой x=8t, y=4t², ( ),

если плотность в каждой точке кривой пропорциональна корню квадратному из ординаты этой точки (коэффициент пропорциональности к=1/2).

Решение

Воспользуемся в этом случае формулой

, где - плотность. В нашем случае

Найдем

, .

Тогда

(ед).

Пример 17.

Вычислить работу, совершаемую силой при перемещении материальной точки по дуге кривой от точки О(0,0) до точки А(2,10).

Решение

Воспользуемся формулой

.

Подставляем данные задачи в эту формулу

.

Найдем

.

Тогда

(ед).

Индивидуальные задания для самостоятельной работы.

I. Изменить порядок интегрирования в двойном интеграле. Область интегрирования изобразить на чертеже.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

1.11.

1.12.

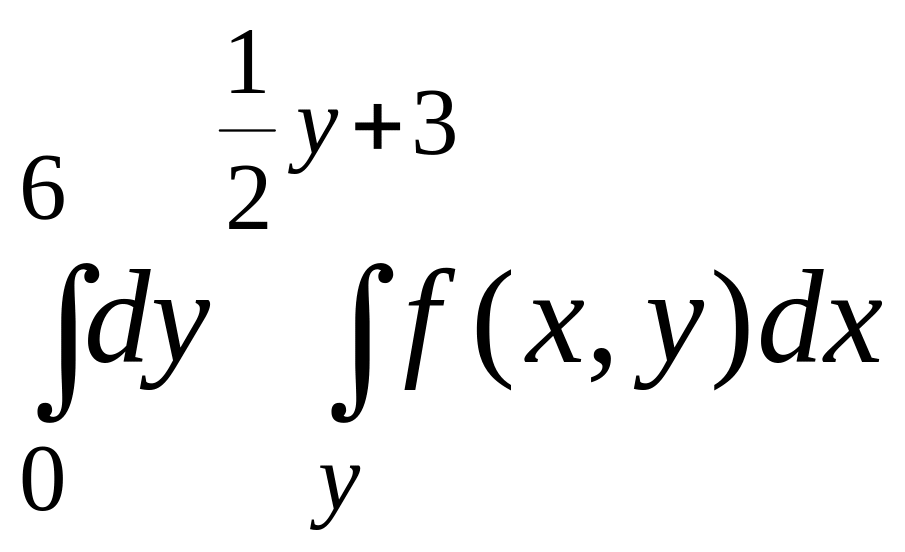
1.13.

1.14.

1.15.

1.16.

1.17.

1.18.

1.19.

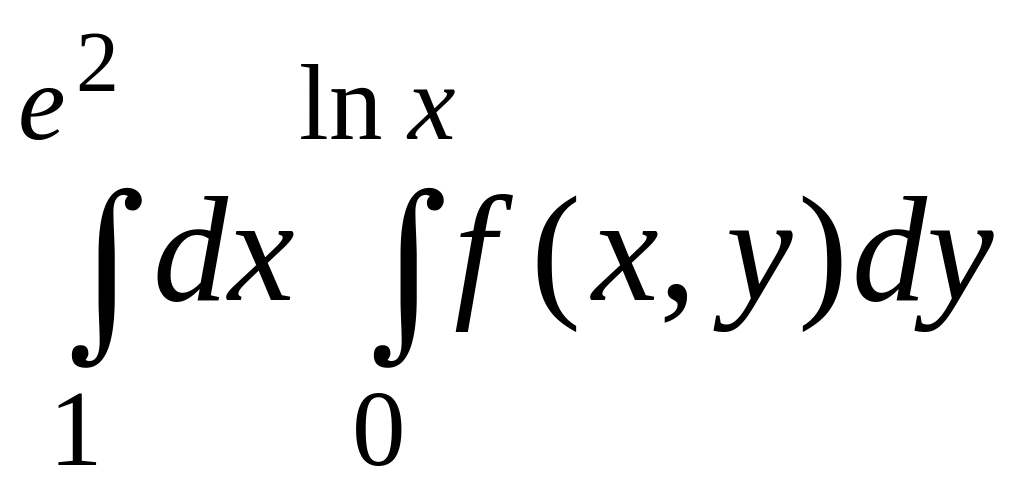
1.20.

II. Пользуясь двойным интегралом, найти площадь фигуры, ограниченной линиями. Сделать чертеж.

2.1. y = x, x = 2, xy = 1

2.2. xy = 6, x+y = 7

2.3. y = -x²+4x-1, y = -x-1

2.4. y = x²+2x, x-y = -2

2.5. y = x, y = 2x, x+y = 6

2.6. y² = x, x+y = 2

2.7. y = x², y = 4-x²

2.8. x = 4

2.9. ,

2.10. x = y², 4x-6y+2 = 0

2.11. x = 9

2.12. y² = 2x+1, y = x-1

2.13. y = x², x+y = 2, x = 2

2.14. y = x², y = 3-2x

2.15. y = 2x-2, x+y = 7, y = 0, y = 2

2.16. y-x = 0, 2x-y = 6, y = 0

2.17. x+y = 2, y = 0

2.18. y = x², y = 2x

2.19. , x = 0, y = 0

2.20. x = y², y = x³

III. С помощью тройного интеграла вычислить объем тела, ограниченного данными поверхностями. Область интегрирования изобразить на чертеже.

3.1. z = 4-y², z = y²+2, x = -1, x = 2

3.2. z = x²-y², z = 0, x = 3

3.3. z = x²+y², z = x²+2y², y = x, y = 2x, x = 1

3.4. z = x, z = 0, x²+y² = 4,

3.5. z = y-x², 4 x² = y, y = 1, z = 0

3.6. z = x²+y²+1, x = 2, y = 3, x = 0, y = 0, z = 0

3.7. z = x²+y², x+y = 1, x = 0, y = 0, z = 0

3.8. z = 2x²+y², x+y = 2, x = 0, y = 0, z = 0

3.9. z = x²+y², y = x², y = 1, z = 0

3.10. z = 4-x², , x = 0, y = 0, z = 0

3.11 z = x² + y², y = , x + y =2, z = 0, x =0

3.12 z = 9-y², 3x+4y = 12, x = 0, y = 0, z = 0, y 0

3.13 z = 4-x, y = 4x², y = 0, z = 0

3.14 z = 4-y², , z = 0

3.15 z=x²+y², , x+y = 2, z = 0, y = 0

3.16. z = 3y, z = 0, x+y = 4,

3.17 x = 15-z-y, z = 0, x = 5, y = 5

3.18. z = x², z = 0, 2x-y = 0, x+y = 9

3.19 z = y²-x², z = 0, y = 3

3.20 z = x²+y²+1, x = 4, y = 4, x = 0, y = 0

IV. Вычислить криволинейные интегралы вдоль заданных контуров.

4.1 , где L – отрезок прямой от точки О(0,0) до точки B (4,3)

4.2 , где L – отрезок прямой от точкиA(-1,1) до точки B (1,1)

4.3 , где L – дуга параболы y = x² от A(-1,1) до B(1,1)

4.4 , где L – отрезок прямой от A(1,2) до B(2,4)

4.5 , где L – отрезок прямой от A(0.-2) до B(4,0)

4.6 , где L – дуга циклоиды

4.7 , где L – отрезок прямой, соединяющей точки M(2,0) и N(4,2)

4.8 , где L – отрезок прямой, соединяющей точки O(0,0) и A(4,3)

4.9 , где L – отрезок прямой, соединяющей точки O(0,0) и A(1,2)

4.10 , где L – дуга кривой

4.11 , где L – окружность x² + y² = 4

4.12 , где L – отрезок прямой от точки A(0,0) до B(1,2)

4.13 , где L – отрезок прямой от точки M(0,1) до B(2,3)

4.14 , где L - отрезок прямой y = x от точки O(0,0) до B(2,1)

4.15 , где L – отрезок прямой от точки A(4,0) до точки B(4,2)

4.16 , где L – дуга параболы y=x² от точки А(0,0) до точки B (2,4)

4.17 , где L – отрезок прямой, соединяющей точки О(0,0) и А(0,2)

4.18 , где L – отрезок прямой от точки А(3,2) до точки B(4,4)

4.19 , где L – отрезок прямой от точки А(0,2) до точки B(2,0)

4.20 , где L – отрезок прямой от точки А (1,0) до точки B(0,1)

V. Вычислить криволинейные интегралы вдоль заданных контуров.

5.1 вдоль дуги L окружности

от точки A(5,0) до B(0,5)

5.2 вдоль дуги L кривой y = lnx от точки A(1,0) до B(e,1)

5.3 вдоль отрезка прямой L=AB, где A(2,0), B(4,5)

5.4 вдоль дуги L кривой y = 2x² от точки A(0,0) до B(1,2)

5.5 вдоль дуги L кривой y=x² от точки A(-1,1) до B(1,1)

5.6 вдоль дуги L кривой y = e^-x. От точки A(0,1) до B(-1,e)

5.7 вдоль отрезка L=AB от точки A(1,2) до B(2,4)

5.8 , где L – дуга окружности x =2cos t, y =2sin t, расположенная в первой четверти.

5.9 , вдоль дуги L кривой y=x² от точки A(1,-1) до B(1,1)

5.10 , где L – контур треугольника, образованного осями координат и прямой 3x + 2y = 6 /по ходу часовой стрелки/

5.11 , где L – дуга кривой y=x² от точки О(0,0) до B (2,4)

5.12 вдоль контура четырёхугольника ABCD с вершинами A(0,0), B(2,0), C(4,4), D(0,4), обходя его против часовой стрелки

5.13 вдоль отрезка L=AB от точки A(0,0) до B(2,3)

5.14 вдоль ломаной L=OAB, где O(0,0), A(2,2), B(2,0)

5.15 -xdy вдоль ломаной L=OAB, где O(0,0), A(4,2), B(4,4)

5.16 где L - отрезок прямой AB от точки A(0,0) до B(3,6)

5.17 вдоль отрезка прямой линии от точки М(0, ) до

N ( ,0)

5.18 вдоль ломаной L=OAB, где O(-1,1), A(0,0), B(2,2)

5.19 вдоль ломаной L=ABC, где A(1,2), В(1,5), С(3,5)

5.20 вдоль кривой y=x² от точкиO(0,0) до A(1,1)