2.Стационарное магнитное поле постоянных токов. Основные уравнения. Общая задача расчета.

Постоянное (или стационарное) магнитное поле - это магнитное поле, неизменяющееся во времени .

1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.

2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.

3. Магнитное поле вихревое, т.е. не имеет источника.

Основные уравнения стационарного электромагнитного поля.

Стационарным называют неизменное во времени электромагнитное поле, создаваемое постоянным током. Оно описывается системой дифференциальных уравнений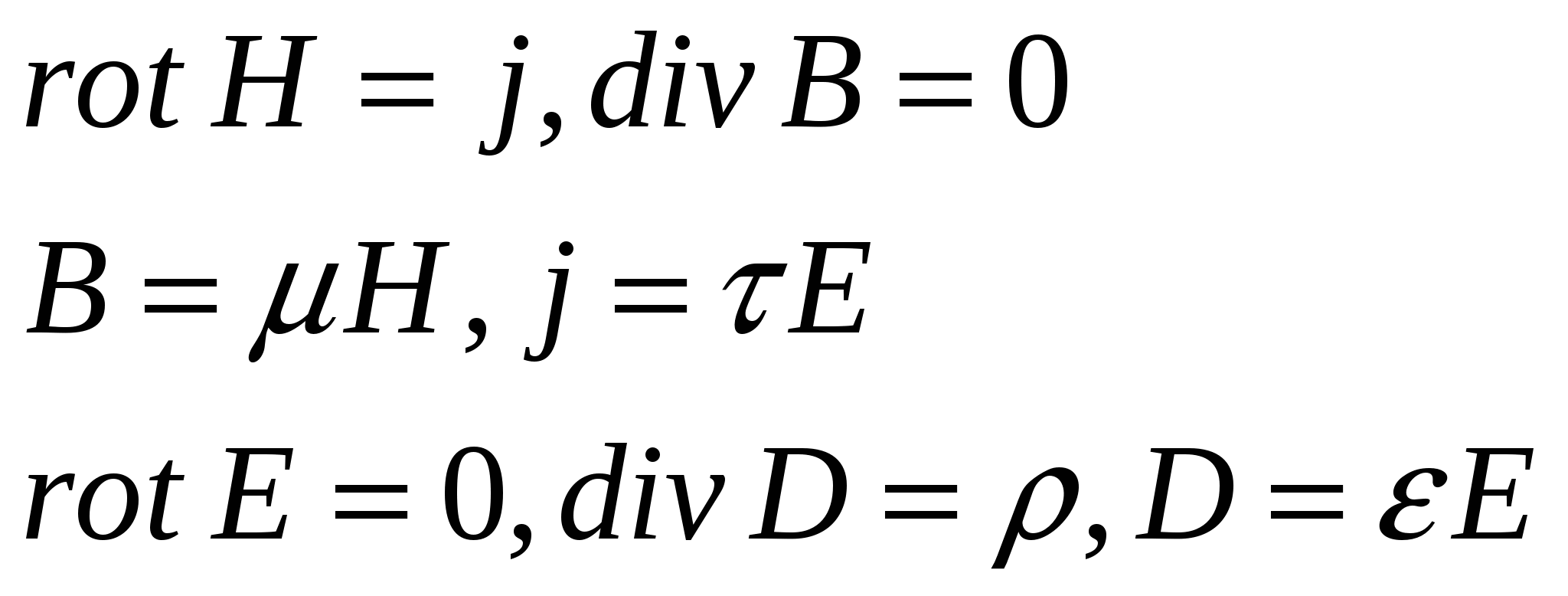

В системе можно выделить две группы уравнений  ,одна из которых  содержит только векторы электрического поля  , 

а другая  только магнитного поля  . При наличии постоянного тока эти группы уравнений связаны соотношением  . Из уравнений группы   

следует, что электрическое поле постоянного тока, как и электростатическое, является потенциальным, а из уравнений группы а следует, что магнитное поле постоянного тока является вихревым.

Общей задачей расчета магнитного поля постоянных токов является определение вектора напряженности магнитного поля или вектора магнитной индукции в каждой точке пространства по заданному распределению тока. Эта задача решается определением векторного потенциала как функции координат.

Билет №10

1. Теорема Остроградского. Теорема Стокса.

Формула Остроградского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

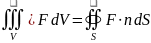
то есть интеграл от дивергенции векторного поля F {\displaystyle \mathbf {F} }, распространённый по некоторому объёму V {\displaystyle V}, равен потоку вектора через поверхность S {\displaystyle S}, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

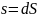где  {\displaystyle \omega } и  {\displaystyle s} — дифференциалы объёма и поверхности соответственно. В современной записи  {\displaystyle \omega =d\Omega } — элемент объёма,  {\displaystyle s=dS} — элемент поверхности. P=P(x, y, z),Q=Q(x, y, z), R=R(x, y, z){\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)} — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

Обобщением формулы Остроградского является формула Стокса.

Теорема Стокса.

Теорема Стокса является одной из важных теорем векторного анализа. Она устанавливает связь между циркуляцией поля по любому контуру L и потоком вихря поля через любую поверхность, натянутую на контур L.

Теорема. Циркуляция поля  по контуру L равна потоку вихря поля через любую поверхность S, лежащую в векторном поле и имеющую своей границей контур L:

                                                  

При этом предполагается, что на поверхности S все частные производные первого порядка от функции   – непрерывны. Нормаль  выбрана к поверхности S так, что бы циркуляция рассматривалась в положительном направлении.