- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§4 Определённый интеграл.
Определение определённого интеграла. Пусть функция определена на отрезке
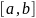 ,
.
Разобьём этот отрехок на n
произвольных частей точками a=
,
.
Разобьём этот отрехок на n
произвольных частей точками a= .
В каждом из полученных частичных
отрезков [
.
В каждом из полученных частичных
отрезков [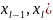 выберем произвольную точку
выберем произвольную точку
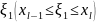 и составим сумму (1)
и составим сумму (1)
|
(1) |
где
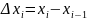 .
Сумма вида (1) называется интегральной
суммой для функции
на
.
Сумма вида (1) называется интегральной
суммой для функции
на
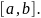
Обозначим
через
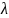 длину наибольшего частичного отрезка
разбиения:
длину наибольшего частичного отрезка
разбиения:
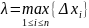 .
.
Определение. Если существует конечный предел I интегральной суммы (1) при 𝜆→0, то этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается следующим образом:
I=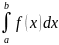 или
или
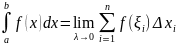
В этом случае функция называется интегрируемой на Числа a и b нахываются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, х – переменной интегрирования.
Для интегрируемой функции достаточно её непрерывности на отрезке
Пример
1. Используя
определение, вычислить интеграл
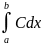 ,
где С
– некоторое число.
,
где С
– некоторое число.
Решение.
Разобьём отрезок [a,b]
на n
произвольных частей точками a= и составим соответствующую интегральную
сумму (1). Так как подынтегральная функция
и составим соответствующую интегральную
сумму (1). Так как подынтегральная функция
 постоянна, то для любого выборв
промежуточных точек
постоянна, то для любого выборв
промежуточных точек
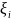 получим интегральную сумму вида
получим интегральную сумму вида
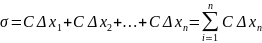 .
Далее имеем
.
Далее имеем
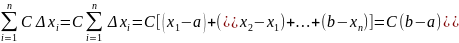
Видим
что интегральная сумма для данной
функции не зависит ни от разбиения, ни
от выбора точек
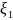 и равна
и равна
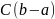 .
Следовательно, и её предел при
.
Следовательно, и её предел при
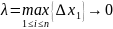 равен
той же
равен
той же
величине.
Таким образом, по определению,
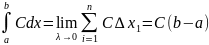
2.Основные свойства определенного интеграла.
10.
По
определению,

20.
По
определению,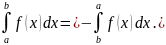
30.
Каковы
бы ни были числа
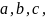 всегда имеет место равенство
всегда имеет место равенство
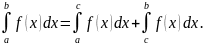
40.Постоянный множитель можно выносить за знак определенного интеграла, т.е.

50.Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.

3. Формула Ньютона-Лейбница. Если функция непрерывна на отрезке и функция является некоторой её первообразной на этом отрезке, то имеет место формула Ньютона-Лейбница

Пример
2.
Вычислить интеграл
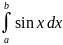
Решение.
Так как одной из первообразных для
функции
 является функция
является функция
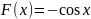 ,
то, применяя формулу Ньютона- Лейбница,
получаем
,
то, применяя формулу Ньютона- Лейбница,
получаем
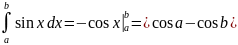
Вычислить интегралы:
254.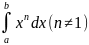
255.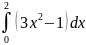
256.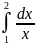
257.
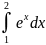
258.
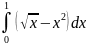
259.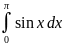
260.

261.
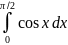
262.
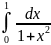
263.
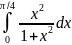
264.
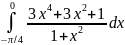
265.
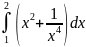
266.
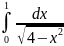
267.

268.

269.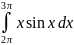
270.

271.
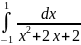
272.
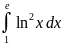
273.
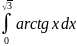
274.
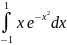
275.
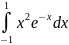
276.
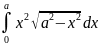
277.
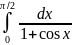
278.

279.
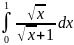
280.
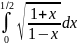
281.
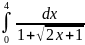
282.
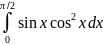
283.
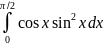
284.
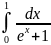
285.

286.
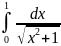
287.
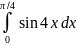
288.
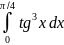
289.

Глава 7.
ЭЛЕМЕНТЫ ВЫСШЕЙ АЛГЕБРЫ
§ 1. Определители
1.
Определители второго порядка. Определение
1.
Определителем
второго порядка называется число,
обозначаемое символом
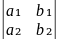 и
определяемое равенством
и
определяемое равенством
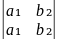 =
1b1-
2b2.
=
1b1-
2b2.
Числа 1, 2, b1, b2 называются элементами определителя.
Вычислить определители:
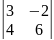 2.
2.
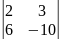 3.
3.
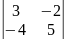 4.
4.

5. 6.
6.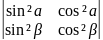 7.
7.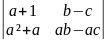
2. Определители третьего порядка. Определение 2. Определителем третьего порядка называется число, обозначаемое символом.
Δ
=

и определяемое равенством
Δ=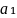 b₂c₃+
b₁c₂
₃
+
c₁b₂
₃
-
c₁b₂
₃
-
b₁
₂c₃
-
₁c₂b₃. (1)
b₂c₃+
b₁c₂
₃
+
c₁b₂
₃
-
c₁b₂
₃
-
b₁
₂c₃
-
₁c₂b₃. (1)
Чтобы запомнить, какие произведения в правой части равенства (1) берутся со знаком «+», а какие со знаком «-», полезно использовать следующее правило треугольников:


Это правило позволяет легко записать формулу (1) и вычислить данный определитель.
Вычислить определители:
8.
 .
9.
.
9.
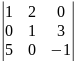 . 10.
. 10.
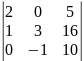 .
.
11.
 .
12.
.
12.
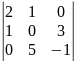 . 13.
. 13.
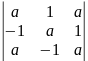 .
.