
- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§3. Сравнение бесконечно малых
Функция
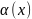 называется бесконечно малой при
называется бесконечно малой при
 (или в точке
˳),
если
(или в точке
˳),
если
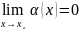 .
Пусть α(x) и
(x)
– две бесконечно малые функции при
.
Пусть α(x) и
(x)
– две бесконечно малые функции при
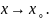 Тогда:
Тогда:
Если
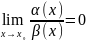 ,
то α(x) называется бесконечно
малой более высокого порядка,
чем
(x);
,
то α(x) называется бесконечно
малой более высокого порядка,
чем
(x);Если
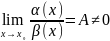 (А
– число), то
и
(x)
называется бесконечно
малой одного порядка;
(А
– число), то
и
(x)
называется бесконечно
малой одного порядка;Если
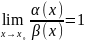 ,
то
и
(x)
называются эквивалентными
бесконечно малыми.
Эквивалентность обозначается так:
,
то
и
(x)
называются эквивалентными
бесконечно малыми.
Эквивалентность обозначается так:
 (x)
при
(x)
при
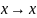 ˳;
˳;Если
 = A
= A
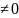 ,
то α(x) называется бесконечно
малой n-го порядка относительно
(x).
,
то α(x) называется бесконечно
малой n-го порядка относительно
(x).
Аналогичные
определения имеют место для случаев
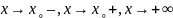 и
и
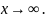
При
сравнении бесконечно малых функций
часто используют символ ο («ο
малое»).
Если функция
в точке
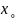 - бесконечно малая более высокого
порядка, чем бесконечно малая
(x)
в этой же точке, то это условно записывается
- бесконечно малая более высокого
порядка, чем бесконечно малая
(x)
в этой же точке, то это условно записывается
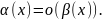 Например,
Например,
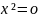 (x) при
(x) при

Пример
1. Доказать, что при
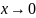 функции
функции
 – бесконечно малая более высокого
порядка, чем
– бесконечно малая более высокого
порядка, чем
Решение.
Действительно,
 ,
так как, по условию, k-1>0.
,
так как, по условию, k-1>0.
Пример
2. Доказать, что при x→0 функции
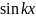 и
и
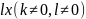 — бесконечно малые одного порядка.
— бесконечно малые одного порядка.
Решение.
В
самом деле,
 .
.
Пример
3. Доказать, что при
функции
и
— эквивалентные бесконечно малые (
при
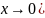
Решение.
Действительно,
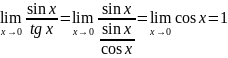 .
.
Пример
4. Определить при
порядок бесконечной малой функции
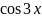 -
-
 относительно
бесконечно малой
.
относительно
бесконечно малой
.
Решение.
Требуется
найти число
такое, чтобы
 был конечным и не равным нулю. Имеем
был конечным и не равным нулю. Имеем
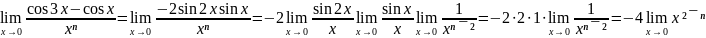 .
.
При
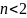
 ,
что не подходит, при
,
что не подходит, при
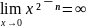 ,
что также не годится. Только при
,
что также не годится. Только при
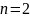
 и искомый предел равен -4, т.е. конечен и
отличен от нуля. Итак,
и функция
и искомый предел равен -4, т.е. конечен и
отличен от нуля. Итак,
и функция
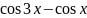 – бесконечно малая второго порядка
относительно бесконечно малой
при
.
– бесконечно малая второго порядка
относительно бесконечно малой
при
.
Глава 5
ДИФФЕРЕНЦИРОВАНИЕ
§ 1. Понятие производной
Определение.
Производной
функции y
= f(x)
в точке xₒ
называется предел при Δx 0
отношения приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
0
отношения приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
Производная обозначается y′ (xₒ) или f′ (xₒ).
Итак, по определению,
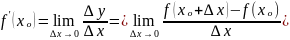
Нахождение производной называется дифференцированием функции.
Пример.
Используя определение производной,
найти производную функции
 в точке
в точке
 .
.
Решение.
Придавая аргументу x
в точке
 приращение
приращение
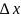 ,
найдем соответствующее приращение
функции:
,
найдем соответствующее приращение
функции:


Составим отношение:
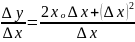
Найдем
предел этого отношения при
 0:
0:
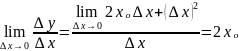
Следовательно,
производная функции
в точке
равна числу
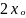 ,
что в принятых обозначениях можно
записать так:
,
что в принятых обозначениях можно
записать так:
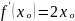
Используя определение производной, найти производные функций в точке
 2.
2.

3.
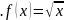 4.
4.
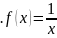
5.
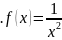 6.
6.

7.
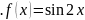 8.
8.
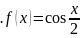
9.
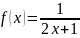 10.
10.
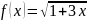
§2. Вычисление производных
I. Правила дифференцирования:
1)
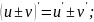
2)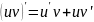 ;
;
3)
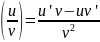
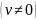 ;
;
4)
если функция
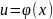 дифференцируема в точке
,
а функция
дифференцируема в точке
,
а функция
 дифференцируема в точке
дифференцируема в точке
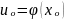 ,
то сложная функция
,
то сложная функция
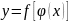 дифференцируема в точке
дифференцируема в точке
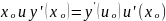 .
.
II. Формулы дифференцирования:
1)
(C)' = 0; 2)
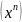 =
=
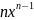 ;
;
3)
 , в частности,
, в частности,
 ;
;
4)
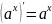 ,
в частности,
,
в частности,
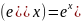 ;
;
5) ; 6) ;
7)
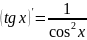 ; 8)
; 8)
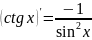 ;
;
9) ; 10) ;
11)
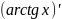 =
=
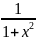 ; 12)
; 12)
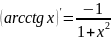 .
.
Пример. Используя правила и формулы дифференцирования, найти производные функций:
1)
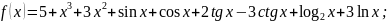
2)
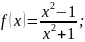
3)
 ;
;
4)
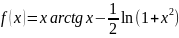 .
.
Решение.
1)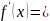
2)
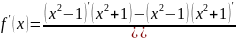 ;
;
3)
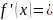 ;
;
4)
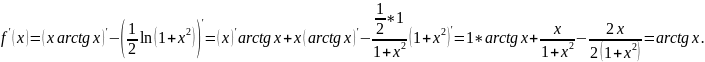
Найти производные функций:
11.
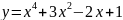 ; 12.
; 12.
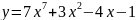 ;
;
13.
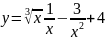 ; 14.
; 14.
 ;
;
15.
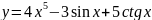 ; 16.
; 16.
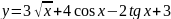 ;
;
17.
 ;
;
18.
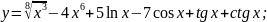
19.
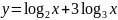 ; 20.
; 20.
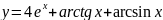 ;
;
21.
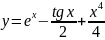 ; 22.
; 22.
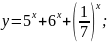
23.
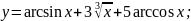 24.
24.
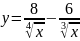 ;
;
25.
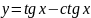 ; 26.
; 26.
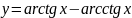 ;
;
27.
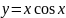 ; 28.
; 28.
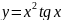 ;
;
29.
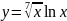 ; 30.
; 30.
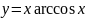 ;
;
31.
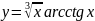 ; 32.
; 32.
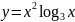 ;
;
33.
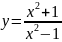 ; 34.
; 34.
 .
.
