
- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§ 2. Предел и непрерывность функции
Определение предела функции. Пусть функция определена на некотором промежутке
 и пусть точка
и пусть точка
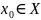 или
или
 .
.
Определение
1.
Число
А называется пределом функции
в точке
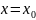 ,
если для любого числа
существует число
,
если для любого числа
существует число
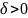 такое, что для всех
такое, что для всех
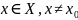 удовлетворяющих неравенству
удовлетворяющих неравенству
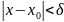 ,
выполняется неравенство
,
выполняется неравенство
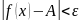 .
.
*Здесь
X
может быть любым промежутком вида
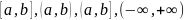 и т.д.
и т.д.
Пример
1.
Используя определение, доказать, что
функция
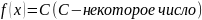 в точке
в точке
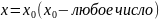 имеет предел, равный С, т.е.
имеет предел, равный С, т.е.
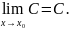
Решение.
Возьмём любое
Тогда для любого числа
выполняется требуемое неравенство
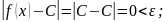 следовательно,
следовательно,
Пример
2.
Используя определение, доказать, что
функция
 в точке
имеет предел, равный
в точке
имеет предел, равный
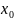 ,
т.е.
,
т.е.
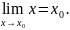
Решение.
Возьмём любое
Тогда если взять
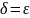 ,
то для всех
,
удовлетворяющих неравенству
,
то для всех
,
удовлетворяющих неравенству
 ;
следовательно,
;
следовательно,
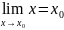 .
.
Пример
3.
Используя определение, доказать, что
функция
 в точке
в точке
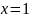 имеет предел, равный единице, т.е.
имеет предел, равный единице, т.е.
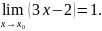
Решение.
Возьмём любое
Задача состоит в том, чтобы по этому
найти такое
,
при котором из неравенства
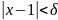 следовало бы неравенство
следовало бы неравенство
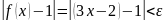 .
Преобразуя последнее неравенство,
получаем
.
Преобразуя последнее неравенство,
получаем
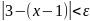 ,
или
,
или
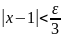 .
Отсюда видно, что если взять
.
Отсюда видно, что если взять
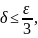 то для всех
,
удовлетворяющих неравенству
,
выполняется требуемое неравенство
то для всех
,
удовлетворяющих неравенству
,
выполняется требуемое неравенство
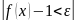 .
Это и означает, что
.
Это и означает, что
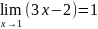 .
В частности, если
.
В частности, если
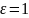 ,
то
,
то
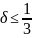 ,
если
,
если
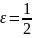 ,
то
,
то
 и т.д.
и т.д.
Свойства пределов.
Теорема
1.
Пусть
функции
 имеют в точке
пределы B
и C.Тогда
функции
имеют в точке
пределы B
и C.Тогда
функции
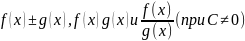 имеют в точке
пределы, равные соответственно
имеют в точке
пределы, равные соответственно
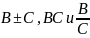 ,
т.е.
,
т.е.
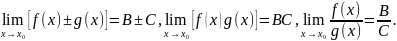
Замечание.
Теорема 1 верна также и в случае, когда
является одним из символов
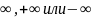 .
.
Пример
4. Найти

Решение.
На основании теоремы 1 (предел суммы и
произведения) имеет
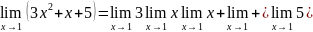 =3*1*1+1+5=9,
так как
=3*1*1+1+5=9,
так как
 (см. примеры 1 и 2).
(см. примеры 1 и 2).
Определение
2.
Функция
называется непрерывной в точке
, если предел функции и её значение в
этой точке равны, т.е.
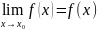 .
.
Пример
5.
Используя определение, доказать
непрерывность функции
 в точке
в точке
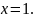
Решение.
Сначала найдём предел данной функции
при
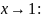
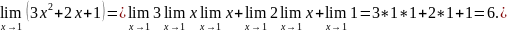
Затем
вычислим значение функции в точке
равны, т.е.
 ;
следовательно, функция непрерывна в
точке
.
;
следовательно, функция непрерывна в
точке
.
Теорема
2. Пусть
функция
непрерывны в точке
.
Тогда функция
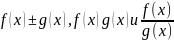 также непрерывны в этой точке (частное
при
также непрерывны в этой точке (частное
при
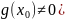 .
.
Пример 6. Найти
 .
.
Решение.
Так как в точке
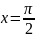 функции
функции
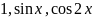 непрерывны, то, по теореме 2, функция
непрерывны, то, по теореме 2, функция
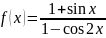 непрерывна в точке
, т.е. предел функции и её значение в этой
точке равны, тогда, переходя к пределу,
получаем
непрерывна в точке
, т.е. предел функции и её значение в этой
точке равны, тогда, переходя к пределу,
получаем
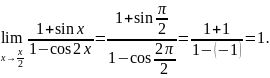
3.
Раскрытие неопределенностей вида
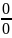 и
и
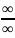 .
.
Пример
7. Найти
 .
.
Решение.
Имеем неопределенность вида
.
Непосредственно теорему 1 (предел
частичного) применить нельзя. Необходимо,
как говорят, раскрыть эту неопределенность.
Для этого разложим числитель на множители
и сократим на общий множитель
 ,
который обращает в нуль знаменатель и
числитель дроби. Получаем
,
который обращает в нуль знаменатель и
числитель дроби. Получаем
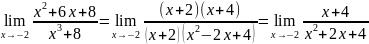
Так
как знаменатель теперь равен нулю, то
неопределенность
раскрыта. Применяя теорему 1, окончательно
находим

Пример
8. Найти
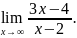
Решение. Имеем неопределенность вида . Разделим на x числитель и знаменатель дроби, а затем применив теорему 1, получим
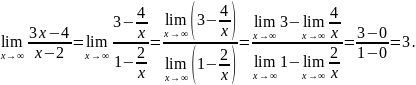
Найти пределы:
234. |
|
235. |
|
236. |
|
237. |
|
238. |
|
239. |
|
240. |
|
241. |
|
242. |
|
243. |
|
244. |
|
245. |
|
246. |
|
247. |
|
248. |
|
249. |
|
250. |
|
251. |
|
252. |
|
253. |
|
254 |
|
255. |
|
256. |
|
257. |
|
258. |
|
259. |
|
260. |
|
261. |
|
262. |
|
263. |
|

 .
.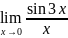 .
.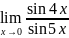 .
.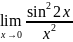 .
. .
. .
.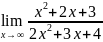 .
.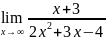 .
.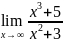 .
.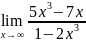 .
.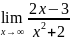 .
. .
.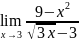 .
.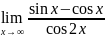 .
.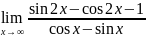 .
.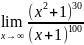 .
.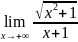 .
.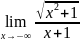 .
.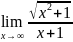 .
.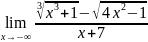 .
. .
.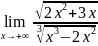 .
.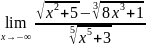 .
.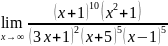 .
.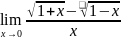 .
. .
.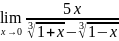 .
.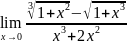 .
.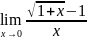 .
. .
.