
- •© Д.А. Захарчук, ю.В. Коваль, 2015
- •Передмова Основні вимоги до підготовки, виконання лабораторних робіт та оформлення звітів
- •Після виконання лабораторної роботи студент повинен:
- •При оформленні звіту студенту необхідно:
- •Для захисту лабораторної роботи студенту потрібно:
- •Похибки прямих та непрямих вимірювань в лабораторних роботах
- •1. Похибки прямих вимірювань
- •1.1. Абсолютні та відносні похибки
- •1.2. Обчислення похибки при непрямих вимірюваннях величин
- •Покажемо підхід Гауса на прикладі функції:
- •Лабораторна робота №41 Визначення декремента згасання коливної системи
- •Теоретичні відомості
- •1. Незгасаючі коливання.
- •2. Згасаючі коливання.
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №42 Визначення швидкості поширення звуку методом стоячих хвиль
- •Теоретичні відомості
- •1. Поширення пружних хвиль
- •2. Акустика
- •3. Інтерференція. Стоячі хвилі
- •Контрольні запитання
- •Лабораторна робота №43 визначення швидкості звуку методом фігур ліссажу
- •Теоретичні відомості
- •1. Звукові хвилі
- •2. Залежність швидкості звуку від температури
- •3. Фігури Ліссажу
- •4 . Опис лабораторного пристрою
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №44 перевірка закону ома для кіл змінного струму
- •Теоретичні відомості
- •Активний та реактивний опори
- •2 . Активна та реактивна потужності
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №45 Дослідження властивостей електромагнітних хвиль
- •Теоретичні відомості
- •1. Шкала електромагнітних хвиль
- •Рівняння Максвелла.
- •3. Опис лабораторного устаткування
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №46 Дослідження перехідних процесів в електричному контурі
- •Теоретичні відомості
- •1. Контур Томсона
- •2. Декремент згасання
- •3. Опис лабораторної установки
- •1. Напруга на конденсаторі
- •2. Градуювання екрану осцилографа.
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 47 Дослідження встановлених процесів у коливальному контурі
- •Теоретичні відомості
- •Вимушені коливання в коливальному контурі
- •2. Амплітудно-частотна характеристика
- •3. Добротність коливального контуру
- •Порядок виконання роботи
- •Контрольні запитання
- •Довідкові таблиці Префікси до одиниць вимірювання
- •Основні фізичні константи
- •Густини деяких твердих тіл
- •Магнітна сприйнятливість та проникність для деяких матеріалів
- •Допоміжна література
- •43018 М. Луцьк, вул. Львівська, 75
Покажемо підхід Гауса на прикладі функції:
![]() . (2.2)
. (2.2)
Лінеаризуючи
![]() в
околі значень
в
околі значень
![]() отримаємо вираз для обчислення повного
диференціала:
отримаємо вираз для обчислення повного
диференціала:
 (2.3)
(2.3)
Значення часткових похідних, взятих по модулю,
 (2.4)
(2.4)
в
теорії похибок називають чутливостями
функції
відповідно до змін величин
![]() .
.
Для визначення абсолютної похибки непрямого вимірювання користуються формулою:
 (2.5)
(2.5)
тобто, похибку непрямого вимірювання шукають згідно з тими ж правилами, що й повний диференціал цієї величини. Формальна відмінність полягає в тому, що всі арифметичні знаки ± при чутливостях змінюються на знаки +, а знаки диференціалів d – на значки похибок Δ.
Наведемо формули для обчислення абсолютних і відносних похибок:
суми:
 , (2.6)
, (2.6)
різниці:
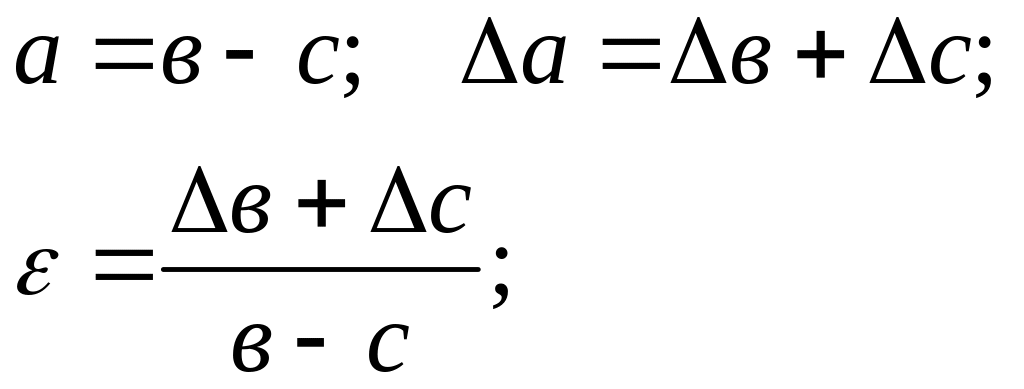 (2.7)
(2.7)
добутку:
 (2.8)
(2.8)
степеня:
![]() ; (2.9)
; (2.9)
дробу:
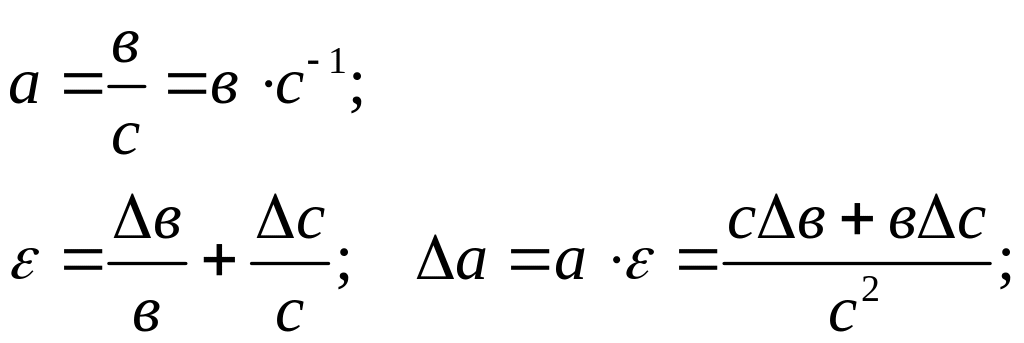 (3.0)
(3.0)
кореня:
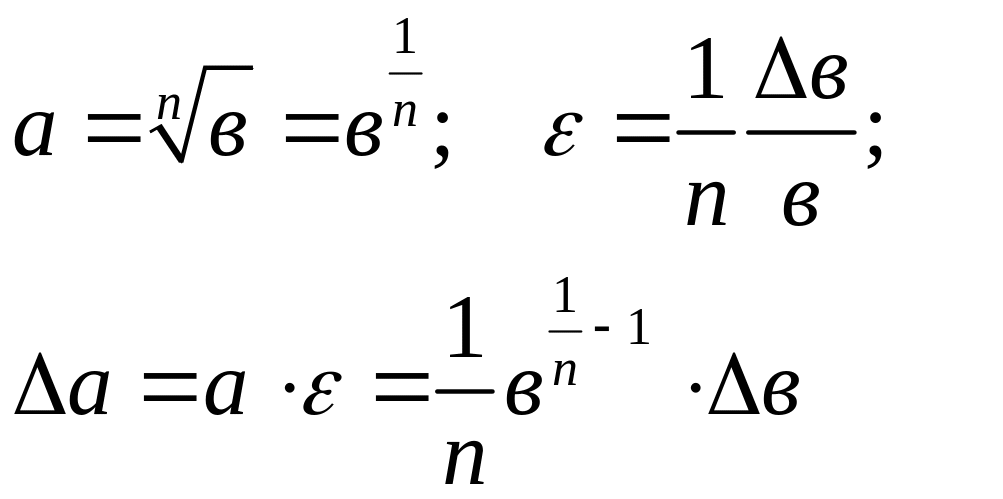 (3.1)
(3.1)
Якщо вираз для шуканої величини не містить значків ”+”чи “-“ (є термом), зручніше спочатку знаходити відносну похибку відповідно до правила: відносна похибка результату дорівнює сумі відносних похибок окремих змінних, взятих із такими коефіцієнтами, в якому степені вони входять у терм.
Наприклад, якщо шукана величина задана виразом:
![]() ,
,
то відносна похибка визначатиметься співвідношенням:
 .
.
Лабораторна робота №41 Визначення декремента згасання коливної системи
МЕТА РОБОТИ: |
навчитись визначати параметри коливної системи. |
ОБЛАДНАННЯ: |
маятник, секундомір. |
Теоретичні відомості
1. Незгасаючі коливання.
Коливанням називається всякий рух або зміна стану тіла, що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, що визначають цей рух або стан тіла. Коливання називають вільними, якщо вони здійснюються за рахунок енергії, яка була надана, за відсутності в наступному зовнішніх впливів на коливну систему. Незважаючи на різну природу коливань, останні можуть бути періодичними, тобто повторюватись через однакові проміжки часу, чи неперіодичними. Форма коливань також може бути різною. Для вивчення та математичного опису найпростішими є гармонічні коливання.
Гармонічні
коливання – це такі
періодичні зміни фізичної величини
![]() ,
при яких її миттєві значення змінюються
в часі за гармонічним законом косинуса
(синуса):
,
при яких її миттєві значення змінюються
в часі за гармонічним законом косинуса
(синуса):
![]() . (1)
. (1)
Аргумент
![]() функції
функції
![]() називають фазою коливань.
Максимальне відхилення
називають фазою коливань.
Максимальне відхилення
![]() від положення рівноваги називають
амплітудою,
коефіцієнт
від положення рівноваги називають
амплітудою,
коефіцієнт
![]() біля часу
біля часу
![]() – циклічною частотою,
а
– циклічною частотою,
а
![]() – початковою фазою
коливань.
– початковою фазою
коливань.
Найменший
проміжок часу
![]() ,
після проходження якого повторюються
значення всіх фізичних величин, що
характеризують коливання, називається
періодом коливання.
,
після проходження якого повторюються
значення всіх фізичних величин, що
характеризують коливання, називається
періодом коливання.
Частотою
коливань
![]() називається кількість повних коливань,
що здійснюються за одиницю часу. Частота
коливань – величина, яка обернена до
періоду коливань:
називається кількість повних коливань,
що здійснюються за одиницю часу. Частота
коливань – величина, яка обернена до
періоду коливань:
![]() .
.
Фізична система, яка моделює гармонічний коливний процес, називається гармонічним осцилятором. Осциляторами є фізичний та математичний маятники, балансир, коливальний контур та інше.
 Математичним
маятником називають
точкове тіло, підвішене на невагомій
нерозтяжній нитці, яке може коливатись
у вертикальній площині під дією сили
тяжіння (див. рис.1). Зважаючи, що довжина
Математичним
маятником називають
точкове тіло, підвішене на невагомій
нерозтяжній нитці, яке може коливатись
у вертикальній площині під дією сили
тяжіння (див. рис.1). Зважаючи, що довжина
![]() дуги кола дорівнює добутку радіуса
дуги кола дорівнює добутку радіуса
![]() на кут
на кут
![]() ,
на який спирається дуга, відповідно до
ІІ закону Ньютона рівняння руху тіла
масою
,
на який спирається дуга, відповідно до
ІІ закону Ньютона рівняння руху тіла
масою
![]() запишемо:
запишемо:
 . (2)
. (2)
Увівши позначення:
![]() , (3)
, (3)
рівняння (2) набуде вигляду:
 . (4)
. (4)
Рівняння (4) нелінійне, тому для його розв’язку необхідно застосовувати спеціальні методи. Однак, при невеликих відхиленнях , коли виконується умова
![]() , (5)
, (5)
рівняння математичного маятника зводиться до диференціального рівняння гармонічного осцилятора:
 .
(6)
.
(6)
Розв’язком
(6) є функція вигляду (1). Період
![]() малих коливань математичного маятника
пов’язаний із циклічною частотою
малих коливань математичного маятника
пов’язаний із циклічною частотою
![]() співвідношенням
співвідношенням
 , (7)
, (7)
отже його визначають за формулою:
 . (8)
. (8)
Якщо
амплітуда коливань велика, період
коливань
![]() відрізнятиметься від
.
Уже при
відрізнятиметься від
.
Уже при
![]() похибка визначення періоду
коливань математичного маятника за
формулою (8) відрізняється від істинного
значення на 2%. Збільшення амплітуди
призводить до зростання похибки.
похибка визначення періоду
коливань математичного маятника за
формулою (8) відрізняється від істинного
значення на 2%. Збільшення амплітуди
призводить до зростання похибки.
Фізичним маятником називають довільне тверде тіло, яке може коливатись у полі тяжіння навколо горизонтальної осі, що не проходить через центр маси цього тіла.
Крутильний маятник (балансир) – тіло, яке може коливатись навколо осі вільного обертання під дією пружини. Фізичний маятник та балансир – основні регулятори ходу в механічних годинниках.
