Метод контурных токов
В основе этого метода лежат законы Кирхгофа и два предположения: в каждом контуре протекают независимые друг от друга расчетные токи, называемые контурными, а ток каждой ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь.
При этих предположениях, вместо уравнений, составленных при непосредственном применении законов Кирхгофа достаточно составить уравнений, т.е. ограничиться составлением уравнений только по второму закону Кирхгофа, так как первый закон выполняется автоматически.
Подробно данный метод рассмотрен в примере выполнения домашнего задания.
Метод двух узлов
Этот
метод применяется для расчета электрических
цепей с двумя узлами (рис.5), между которыми
включены активные и пассивные ветви.
Идея метода состоит в том, что по расчетной
формуле определяется напряжение между
узлами, называемое узловым напряжением
,
а затем по обобщенному закону Ома
рассчитываются токи в ветвях.
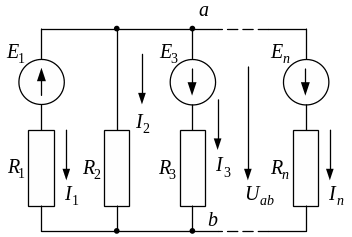
Рис.5. К пояснению метода двух узлов
Выведем
формулу для расчета узлового напряжения.
Положительные направления токов в
ветвях выберем от узла
к узлу
.
Напряжение
– узловое напряжение, общее для всех
ветвей схемы.
Токи в ветвях по закону Ома будут:
;
;
;
…;
Запишем первый закон Кирхгофа для узла . Подставляя значения токов в ветвях, имеем
или
.
Напряжение между узлами
или в общем виде
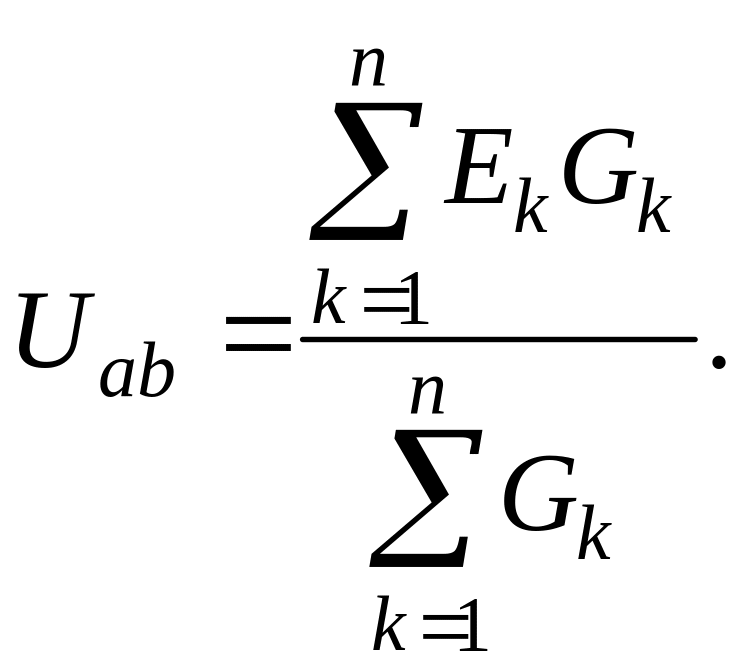
Если
ЭДС направлена к узлу, обозначенному
первым индексом
,
то произведение
записывается со знаком «+», если от узла
– со знаком «
»
независимо от положительных направлений
токов. Если в ветви нет ЭДС, то произведение
.
Токи в ветвях вычисляются по формуле
где со знаком «+» берутся токи и ЭДС, направленные к узлу , а со знаком « » от узла .
Подробно данный метод рассмотрен в примере выполнения домашнего задания.
Энергия и мощность в электрической цепи
Из
определения ЭДС следует, что работа,
совершаемая источником электрической
энергии за время
,
т. е. работа сторонних сил в источнике
по разделению зарядов, равна
На
пассивном участке цепи, т. е. в сопротивлении
нагрузки или, как говорят, в приемнике
электрической энергии, при напряжении
и токе
расходуется энергия
Мощность
характеризует интенсивность преобразования
энергии из одного вида в другой в единицу
времени.
Для цепи постоянного тока мощность источника
а приемника
В
системе СИ единицами измерения энергии
и мощности соответственно являются 1
джоуль (
)
и 1 ватт (
);
1 джоуль равен 1 ватт – секунде (1
).
Баланс мощностей
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии:
где
– сумма мощностей, развиваемых
источниками;
– сумма мощностей всех приемников и
необратимых преобразований энергии
внутри источников (потери из-за внутренних
сопротивлений).
Равенство называется балансом мощности электрической цепи.
Если
положительное направление тока совпадает
с направлением ЭДС и в результате расчета
получено положительное значение тока,
то источник работает в режиме генератора.
Если же получено отрицательное значение
тока, то произведение
отрицательно, т. е. источник работает в
режиме потребителя и является приемником
электрической энергии (например,
электрический двигатель, аккумулятор
в режиме зарядки).