5. Задание к лабораторной работе

Постройте графики функций заданных в соответствии с вашим вариантом.

№ Варианта	Функция
	На плоскости		В пространстве
1
2
3
4
5
6
7
8	Линия задана параметрическими уравнениями ,
9
10
11
12
13
14
15
16
17
18
19
20

Контрольные вопросы

1. Каково основное назначение среды автоматического проектирования MathCad?

2. Какую последовательность действий необходимо выполнить, что бы построить график функции в среде MathCad?

3. Что понимается под форматированием графика?

4. Какие параметры графиков функции можно настроить при помощи панели форматирования?

5. Какие манипуляции можно выполнять с графиками трехмерных функций?

6. Каким образом задается диапазон изменения аргумента функции?

Лабораторная работа № 2 Решение систем уравнений, нелинейных и дифференциальных уравнений в системе MathCad

Цель работы: Научиться в системе MathCad решать системы линейных уравнений, а также нелинейных и дифференциальных уравнений.

1. Решение систем линейных уравнений

1.1. Решение систем линейных уравнений матричным способом

Векторные и матричные операторы и функции системы Mathcad позволяют решать широкий круг задач линейной алгебры. Рассмотрим задачу решения системы из n линейных уравнений матричным способом. Пусть нам дана система уравнений:

Решить систему – значит найти такие числа, при подстановке которых в данную систему получим все n верных равенств. Для этого сначала составляем матрицу A, состоящую из коэффициентов при переменных (размерность ) и матрицу B, состоящую из свободных членов уравнений (размерность ). Перепишем и исходную систему в матричном виде: . Вектор решения можно получить из следующего выражения: . Остается только сделать проверку простой подстановкой корней в уравнения, чтобы убедиться в правильности решения задачи Рассмотрим задание матриц и операции над ними.

Рис. 1.

Для того, чтобы задать матрицу щелкаем мышью ВИД, затем ПАНЕЛИ ИНСТРУМЕНТОВ, далее МАТЕМАТИКА.

Появляется панель МАТЕМАТИКА с различными шаблонами.

Щелкаем на шаблоне матрицы, и появляется панель МАТРИЦЫ с математическими операциями над ними. При помощи мыши выбираем нужную операцию.

Рассмотрим примеры:

Пример 1: Умножить две матрицы.

Задаем матрицы А и В нужного размера

Находим на панели шаблон скалярного произведения

Пример 2: Найти обратную матрицу.

Задаем матрицу А

Матрице В присваиваем обратное значение матрицы А (находим на панели шаблон инверсии )

Находим матрицу B

Пример для самостоятельного решения

Умножить две матрицы и найти обратную для первой матрицы

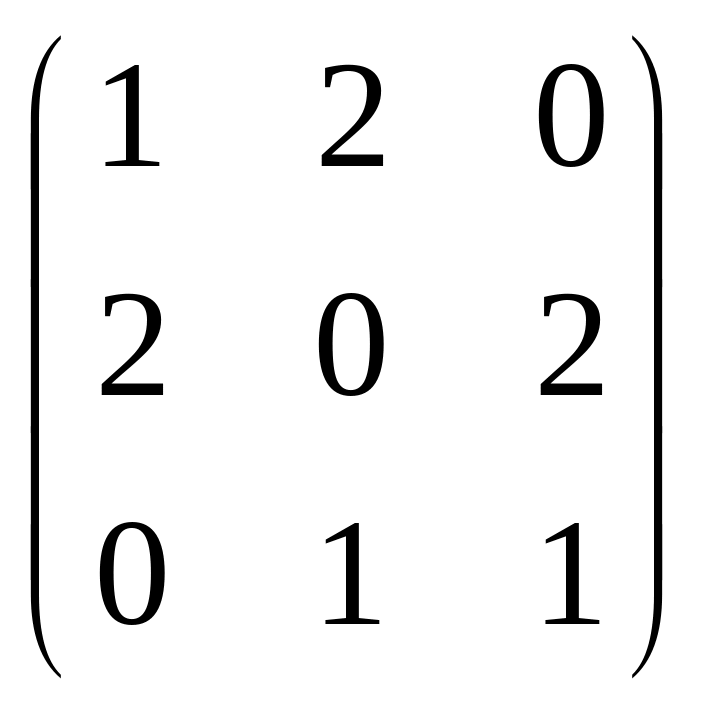
Используя примеры 1 и 2, решим систему уравнений матричным способом.

Присвоение переменной А матрицы, состоящей из коэффициентов при переменных в системе

Присвоение переменной В матрицы, состоящей из столбца свободных членов системы

Матричное решение X, выраженное в матричном виде

Корни системы

Проверка