4 Дослідження лінійних сау з запізненням
4.1 Мета роботи
Метою роботи є дослідження впливу величини запізнювання на якість перехідного процесу і стійкість лінійних САУ.
4.2 Методичні вказівки з організації самостійної роботи студентів
Під час підготовки до лабораторної роботи студенти повинні повторити відповідний лекційний матеріал і дані практичних занять. Ознайомитися з матеріалами що наведені у літературі [3-9], а саме: елементарні ланки "чистого" запізнення, їх часові та частотні характеристики; побудова АФЧХ ланок із запізнення; стійкість і якість систем із запізнення.
Програмою досліджень лабораторної роботи є:
– побудова заданої структурної схеми САУ;
– побудова ЛАЧХ і ЛФЧХ системи без ланки "чистого" запізнення.;
– визначення критичного значення запізнення;
– моделювання системи при заданих значеннях запізнення;
– визначення прямих та частотні показників якості.
Перед виконанням роботи студенти повинні знати визначення критичного значення запізнення і вміти розраховувати показники якості в перехідному режимі.
Лінійними системами з запізненням називають такі системи, які в одній або в декількох ланках мають запізнення в часі зміни вихідної величини стосовно зміни вхідної на постійну величину, що зветься часом запізнення. Ланку з запізненням звичайно можна представити у вигляді послідовно включених звичайної ланки без запізнення і ланки з "чистим" запізненням. Ланка з "чистим" запізненням описується рівнянням виду:
,
(4.1)
де
та
– відповідно величини на вході і виході
ланки,
-
час запізнення.
Передавальна функція такої ланки має вид:
(4.2)
Часові характеристики ланки "чистого" запізнення мають вид
,
(4.3)
Частотна передавальна функція ланки з запізненням дорівнює:
(4.4)
Прикладами ланки "чистого" запізнення є акустична лінія зв'язку (час проходження звуку), також це може бути система автоматичного дозування якої-небудь речовини, переміщуваної за допомогою стрічкового транспортера (час руху стрічки на визначеній ділянці) та ін.
Часові характеристики будь-якої ланки з запізненням будуть такі самі, як і у відповідної ланки, але тільки зрушені по осі часу на величину запізнення. Розглянемо систему з запізненням, структурна схема якої подана на рис. 4.1.
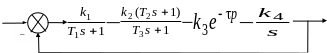
Рисунок 4.1– Структурна схема САУ з запізненням
Передавальна функція розімкнутої системи дорівнює:
, (4.5)
де
– передавальна функція розімкнутої
системи без запізнення;
– коефіцієнт
підсилення розімкнутої системи,
.
Характеристичне рівняння замкнутої системи з запізненням є трансцендентним, тому алгебраїчні критерії стійкості (Гурвиця, Л'єнара-Шипара) у даному випадку незастосовні.
Для дослідження систем із запізнюванням на стійкість використовують частотні методи. Особливо зручні метод Найквіста і його різновид - використання логарифмічних частотних характеристик.
Частотна передавальна функція розімкненої системи:
,
(4.6)
де
–- частотна передавальна функція системи
без запізнення;
– частотна
передавальна функція ланки з "чистим"
запізненням.
Можна
переконатися, що модуль
дорівнює модулю
,
тобто амплітудно-частотні характеристики
системи без запізнення і системи з
запізненням збігаються. Фазочастотна
характеристика системи з запізненням
відрізняється від фазочастотної
характеристики системи без запізнення
на величину
.
(4.7)
ЛАЧХ системи з запізненням цілком збігається з ЛАЧХ тієї ж системи, але без запізнення.
Для
побудови АФЧХ будь-якої лінійної САУ з
запізненням потрібно побудувати
характеристику відповідної звичайної
системи, а потім кожну її точку зрушити
уздовж окружності за годинниковою
стрілкою на кут
,
де
-
значення частоти коливань у даній точці
характеристики. Оскільки на початку
АФЧХ
,
а наприкінці
,
тому початкова точка залишається без
змін, а кінець характеристики асимптотично
навивається на початок координат.
Критичне значення запізнення визначається за формулою:
,
де
- частота зрізу розімкнутої системи без
ланки "чистого" запізнення,
– запас
стійкості по фазі розімкнутої системи
без ланки "чистого" запізнення.
4.3 Опис лабораторної установки
Лабораторна робота виконується в середовище Matlab за допомогою пакету моделювання динамічних систем Simulink. Опис лабораторної установки наведений в пункті 1.3.
4.4 Порядок виконання роботи та методичні вказівки щодо її виконання
Для заданого варіанта (табл. 4.1) побудувати ЛАЧХ і ЛФЧХ системи без ланки "чистого" запізнення, структурна схема якої зображена на рис. 4.1. а побудована Simulink-модель на рис. 4.2.
До складу віртуального лабораторного макету входять наступні блоки:
блок Step (з бібліотеки simulink/Sources) – генератор одиничного ступінчастого сигналу;
блок TransferFunction (з бібліотеки simulink/Continuous) – передавальна функція;
блок Gain (з бібліотеки simulink/Continuous) – задає коефіцієнт підсилення системи;
блок Subtract (з бібліотеки simulink/Math Operations) –для створення від’ємний зв’язку;
блок Scope (з бібліотеки simulink /Sinks) – осцилограф для візуалізації процесу моделювання.
Рисунок 4.2 – Simulink-модель САУ без ланки "чистого" запізнення
З'ясувати, чи буде система стійкою при заданих значеннях параметрів. Для цього провести моделювання та проаналізувати перехідну характеристику САУ.
Визначити критичне значення запізнення. Для цього знайти запас стійкості по фазі та частоту зрізу (рис. 4.3). Для побудови частотних характеристик можна скористуватись графічним інтерфейсом Simulink LTI-Viewer.
Рисунок 4.3 – ЛАЧХ та ЛФЧХ системи без ланки "чистого" запізнення
Додати ланку запізнення в модель – блок Transport Delay з бібліотеки simulink/Continuous (рис. 4.4). Для зміни значення запізнення необхідно відкрити блок для редагування (два рази натиснувши на ньому лівою кнопкою миші) та змінити значення Time Delay на розраховане критичне значення запізнення.
Рисунок 4.4 – Simulink-модель САУ з ланкою "чистого" запізнення
Провести моделювання системи при наступних значеннях запізнення:
,
,
,
,
.
Таблиця 4.1- Вихідні дані для виконання роботи
-
№вар.
К
Т1
Т2
Т3
1
100
2,4
0,8
0,10
2
90
2,6
1,0
0,15
3
80
2,8
1,2
0,20
4
100
3,2
1,4
0,20
5
90
2,8
1,4
0,20
6
80
3,2
1,8
0,25
7
70
1,0
І,6
1,20
8
100
1,4
0,8
0,1
4.5 Зміст звіту
Загальні правила оформлення матеріалів звіту оговорюються у вступі до методичних вказівок.
В теоретичній частині треба привести навести часові та частотні характеристики ланки чистого запізнювання.
В експериментальній частині привести графіки перехідного процесу при різних значеннях величини запізнювання, розрахунок показників якості системи.
У висновках проаналізувати, як впливає величина запізнення на якість перехідного процесу і стійкість системи.
4.6 Контрольні запитання та завдання
1. Що таке "чисте запізнення"? Приклади реальних систем із запізненням.
2. Тимчасові і частотні характеристики систем із запізненням.
3. Як впливає на частотні характеристики лінійної системи введення ланки з запізненням?
4. Як впливає збільшення величини запізнення на прямі і частотні показники якості?
5.Як оцінити стійкість систем із запізненням.
6. Як будується АФЧХ систем із запізненням?