Производные высших порядков
Пусть f(x)
– дифференцируема в интервале
.
Если ее производная
- тоже дифференцируема в интервале (a,
b), то можно рассмотреть
функцию
,
которая называется второй производной
функции f(x).
Аналогично можно
рассмотреть
- третья производная функции f(x)
и т.д.
Для n
– ой производной: 
Теорема: Для функции f(x), имеющей производные вплоть до n– го порядка в точке x0 справедлива формула Тейлора:
где 0((x-x
)n - бесконечно
малая относительно
.
Пример: Разложить
функцию
с
помощью формулы Тейлора, принимая
.
Если взять х=1, то можно вычислять число e со сколь угодно большой точностью.
Признак экстремума (через знак второй производной)
Теорема: Если для функции f(x) в некоторой точке
,
,
то в точке x0
имеется экстремум , причем если
- точка минимума
функции
- точка максимума
функции.
Пусть
если
(f(x)
справа от
возрастает)
если
(f(x)
слева от
убывает)
точка
минимума функции f(x).
Исследование функций
График функции y
= f(x)
называется выпуклым (вогнутым)
в области D
R,
если соответствующий отрезок кривой y
= f(x)
расположен ниже (соответственно выше)
касательной в каждой точке области D.
Мнемоническое правило:
Знак
“+” – вода из “чашки” не выливается
– функция вогнута,
Знак
“-” – вода из “чашки” выливается –
функция выпукла.
Примем без доказательства.
Точка на графике
кривой
,при
переходе через которую кривая из выпуклой
становится вогнутой (или наоборот)
называется точкой перегиба кривой.
Очевидно, что точки
перегиба, это точки на кривой, где
Асимптота – это прямая, лучом которой в окрестности бесконечно удаленной точки можно приближенно заменить соответствующий участок кривой.
Если прямая
- асимптота кривой
при
(бесконечно малая)
Деля на x:
Пример:
Исследовать функцию
и построить ее график.
Область определения:
функция непрерывна в области определения.
Поведение на границах области:
-
вертикальная асимптота.
Пересечение с осями:
Экстремумы функции:
Точки перегиба:
Асимптоты:
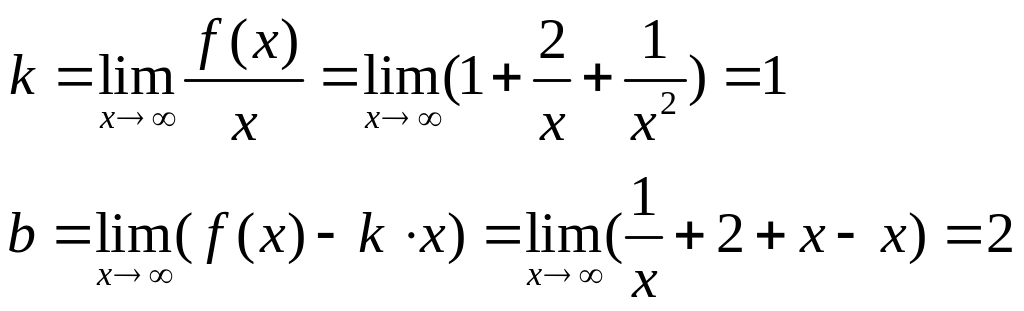
Асимптота:
Теорема Ролля
: Если функция f(x)
непрерывна на
,
дифференцируема на (a,
b) и
то существует хотя бы одна точка
Если
Если
найдется хотя бы одна точка
,в
которой достигается локальный экстремум.
Очевидно,
.
Теорема Коши:
Если функции f(x)
и
:
непрерывны на отрезке
,
дифференцируемы на интервале (a,
b),
,
тогда найдется такая точка
в которой выполняется
-
(1)
Введем вспомогательную функцию
Не трудно убедиться, что она удовлетворяет всем условиям теоремы Ролля.
Значит найдется
Теорема Лагранжа:
Если функция f(x)
непрерывна на отрезке
,
дифференцируема на интервале(a,
b), тогда найдется
такая точка
(2)
Эта теорема –
частный случай теоремы Коши, если взять
Так как
Задача:
С помощью формулы Лагранжа (2) найти
приближенное значение
Возьмем
.
Условия теоремы Лагранжа выполняются,
значит существует
Так как
