Аппроксимация биномиального распределения нормальным

Давайте вспомним: биномиальное распределение описывает количество наступлений некоторого события в п независимых попытках. Биномиальное распределение никогда не может в точности совпадать с нормальным в силу двух причин. Во-первых, любое нормальное распределение может давать наблюдаемые результаты в виде чисел с дробной частью (например, 7,11327), в то время как биномиально распределенная величина X может принимать только целые значения (допустимым является, например, число 7). Кроме того, биномиальное распределение при π, отличном от 0,5, всегда асимметрично, в то время как нормальное распределение во всех случаях сохраняет идеальную симметрию.

Однако биномиальное распределение можно хорошо аппроксимировать с помощью нормального распределения, если п достаточно велико, а вероятность π не слишком близка к 0 или 1.

(Если π близко к 0 или 1, приближение к нормальному распределению с ростом n оказывается более медленным, что обусловлено асимметрией биномиального распределения с редкими или почти определенными событиями. Хорошим приближением для биномиального распределения при больших n и близких к 0 значениях π оказывается распределение Пуассона, которое будет рассмотрено в следующем разделе. Центральная предельная теорема, которую мы рассмотрим в главе 8, поясняет возникновение нормального распределения при объединении результатов большого числа независимых случайных попыток).

Это помогает вычислять вероятности (того, что некоторая величина меньше определенного значения, превышает его, находится между двумя значениями или вне интервала между двумя значениями) для биномиального распределения путем замены многих сложных и трудоемких вычислений (по рассмотренной ранее формуле для вычисления вероятностей, имеющих бино­миальное распределение величин) на более простые вычисления (с использованием формул для нормального распределения).

Как, однако, выбрать такое нормальное распределение, которое, достаточно близко к данному биномиальному распределению? Хорошим выбором будет использование нормального распределения с такими же значениям среднего и стандартного отклонения, как и у подлежащего аппроксимации биномиального распределения. Поскольку мы уже знаем, как вычислять среднее значение и стандартное отклонение для биномиального распределения (этот вопрос рассмотрен ранее), а также как вычислять вероятности для нормального распределения с известными средним и стандартным отклонениями (см. раздел выше), вычисление приближенных значений вероятности для имеющих биномиальное распределение величин уже не должно представлять особых сложностей.

Рассмотрим пример аппроксимации биномиального распределения нормальным. Предположим, что п равно 100 и π равно 0,10. Распределение вероятностей, вычисленных с использованием формулы для биномиального распределения, показано на рис. 7.4.1.

Распределение достаточно явно имеет присущую нормальному распределению колоколообразную форму. Несмотря на то, что распределение все еще остается дискретным, достаточно очевидно, что эта дискретность не является его главным свойством.

Для того чтобы аппроксимировать биномиальное распределение (с дискретными целочисленными значениями) с помощью нормально распределенной случайной величины (непрерывной), отложим от каждого значения вправо и влево 1/2, чтобы включить в рассмотрение все числа, расположенные вокруг целых чисел.

Здесь предполагается поиск вероятностей для имеющего биномиальное распределение количества X наступлений события. Если необходимо вычислить вероятности биномиальной доли, или процента, р, следует сначала перейти к количеству X. Например, вероятность наблюдения “по меньшей мере 20% из 261” — это то же, что и наблюдение “по меньшей мере 53 из 261”, поскольку в этом случае требуется, по меньшей мере 0,20 * 261 = 52,2 наблюдений, причем возможны только целые значения.

Например, для аппроксимации вероятности того, что некоторая биномиально распределенная величина X равна 3, необходимо найти вероятность того, что нормально распределенная (с теми же значениями среднего и стандартного отклонения) величина попадает в интервал от 2,5 до 3,5. Такое расширение необходимо в связи с тем, что для любой нормально распределенной случайной величины вероятность ее точного равенства числу 3 равна нулю, и в то же время все значения нормально распределенной случайной величины в интервале от 2,5 до 3,5 округляются до целого числа 3. Аналогичным образом вероятность того, что биномиально распределенная случайная величина примет значение в интервале от 6 до 9, соответствует вероятности того, что нормально распределенная (с тем же значениями среднего и стандартного отклонения) величина попадает в промежуток от 5,5 до 9,5. Вероятность того, что значение окажется вне ограниченного двумя числами интервала, равна, как обычно, единице минус вероятность попадания в этот интервал.

Сравните графики, показанные на рис. 7.4.1 (n = 100) и рис. 7.4.2 (n = 10). Из них видно, что при меньших значениях п распределение менее похоже на нормальное. Кроме того, при меньших п больше сказывается дискретность распределения.

Пример. Быстрые и медленные микропроцессоры

Производственный процесс часто контролируется не так хорошо, как хотелось бы. Это утверждение относится и к производству используемых в микрокомпьютерах сложных микропроцессорных интегральных микросхем, в которых более 1 000 000 транзисторов размещаются на кремниевой подложке площадью в 1/4 квадратного дюйма. Несмотря на тщательный контроль, получаемые микросхемы отличаются друг от друга: одни оказываются более быстродействующими, чем другие.

В традициях программного обеспечения предыдущих поколений, когда утверждалось: "Это не ошибка, это такая особенность!", произведенные микросхемы сортируются по быстродействию и цены на них устанавливаются соответствующим образом (более быстрые схемы дороже и стоят). В каталоге указывают два типа изделий: со скоростью 300 мегагерц (более медленные) и 500 мегагерц (более быстрые).

Используемое некоторой компанией оборудование в 80% случаев производит медленные микросхемы, а быстрые микросхемы составляют остальные 20% объема выпускаемой продукции. Каждая схема оказывается быстрой или медленной независимо от свойств схем, произведенных до и после нее. Представим себе, что сегодня нужно отгрузить 1000 медленных микросхем и 300 быстрых микросхем; возможно, при этом какие-то микросхемы останутся в избытке. Выпуск какого количества микросхем необходимо запланировать?

Если в производственный план внести выпуск 1300 микросхем, следует ожидать, что 80% (1040 микросхем) окажутся медленными, а 20% (260 микросхем) будут быстродействующими. Медленных схем окажется достаточно, однако, в среднем быстродействующих будет мало.

Поскольку очевидно, что минимально необходимый объем плана выпуска определяется быстродействующими микросхемами, на их количестве и следует основывать расчеты. Сначала находим 300/0,20 = 1500. Отсюда следует, что если в план внести выпуск 1500 микросхем, можно ожидать, что 20% из них (300 штук) окажутся быстродействующими. Это позволит в среднем достичь соответствия поставленной цели. Однако, к сожалению, при этом вероятность выполнения поставленной задачи по выпуску быстродействующих микросхем составит только около 50%!

Предположим теперь, что запланирован выпуск 1650 микросхем. Чему равна вероятность того, что цель будет достигнута? Для получения ответа на этот вопрос прежде всего сформулируем его как задачу на вычисление вероятности.

Дана биномиально распределенная случайная величина (количество выпущенных быстродействующих микросхем) с общим количеством микросхем n = 1650 и вероятностью того, что микросхема окажется быстродействующей, π = 0,20. Необходимо найти вероятность того, что эта случайная величина примет значение, равное по меньшей мере 300, но не превышающее 650.

(Это ограничение обусловлено тем, что выпуск более чем 1650 - 1000 = 650 быстрых микросхем означает, что выпущено менее чем 1000 медленных микросхем; в этом случае не удастся достичь поставленной цели с точки зрения количества медленных микросхем).

Если решать эту задачу, непосредственно вычисляя вероятность для биномиального распределения, придется рассчитывать вероятности для 300, 301, 302 и т.д. схем. Аппроксимирование биномиального распределения нормальным позволяет получить ответ значительно быстрее с помощью таблицы стандартного нормального распределения. При этом необходимо знать среднее значение и стандартное отклонение для количества произведенных быстрых микросхем.

µ = n*π = 1650*0.20 = 330

σ = = = 16,25.

Необходимо также нормировать предельные значения для количества требуемых быстрых микросхем, 300 и 650 (после расширения интервала на 0,5 получаем 299,5 и 650,5). Нормирование проводится с использованием уже найденных среднего значения и стандартного отклонения:

z₁ = (299.5-330)/16.25 = -1,88

z₂ = (650.5-330)/16.25 = 19,73.

Соответствующие этим нормированным величинам значения вероятности находим в таблице стандартного нормального распределения. Для z₁ = -1,88 это 0,030. Поскольку число z₂ = 19,73 лежит за пределами таблицы, соответствующую ему вероятность принимаем равной 1. Вычитая меньшую вероятность из большей, находим вероятность того, что случайная величина будет лежать в указанных пределах, и таким образом получаем необходимый ответ: 1 - 0,030 = 0,970. Отсюда можно сделать вывод о том, что если в производственный план включить выпуск 1650 микросхем, то с вероятностью 97% цель отгрузить 300 быстродействующих микросхем и 1000 медленных микросхем будет достигнута.

Пример. Социологический опрос избирателей

Вероятности помогают также понять, что происходит “за кулисами” действия, разворачивающегося в реальной жизни. Попробуем разобраться, что может происходить при проведении социологического исследования. Воспользуемся для этого анализом сценариев вида что если.... .

Фирма, специализирующаяся на социологических исследованиях и проведении опросов по телефону, получила заказ на опрос общественного мнения для выяснения того, будет ли новая инициатива местных властей поддержана при голосовании во время следующих выборов. Фирма принимает решение опросить 800 выбранных случайным образом человек, которые, видимо, примут участие в голосовании. В результате опроса установлено, что 437 человек собираются голосовать "за". Вот теперь и возникает вопрос "Что если?", который в данном случае формулируется так: если бы мнения всех избирателей разделились поровну между "за" и "против", с какой вероятностью можно было бы ожидать, что именно столько или более людей, попавших в выборку для опроса, ответили бы, что они собираются голосоватъ "за"? Вы ищете ответ, на этот вопрос вместе со своим сотрудником!

• Ваш сотрудник: "Эти доли, похоже, достаточно близки: 437 из 800 очень близко к распределению голосов 50 на 50, что соответствовало бы 400 из 800".

• Вы: "А мне кажется, что 437 гораздо больше, чем 400. Нужно попробовать выяснить, можно ли дополнительные 37 голосов "за" объяснить только случайностью".

• Ваш сотрудник: "Хорошо. Можно предположить, что каждый из опрошенных с одинаковой вероятностью может быть "за" или "против". Тогда можно рассчитать вероятность того, что результат "за" составит 437 или более".

• Вы: "Это можно. Если вероятность окажется больше 5 или 10%, дополнительные 37 ответов "за" можно будет считать случайными. Но если вероятность будет мала, например меньше 5% или даже меньше 1%, то, видимо, здесь присутствует нечто большее, чем просто случайность".

Для того чтобы произвести соответствующие вычисления, предположим, что некоторая величина X описывает следующую биномиально распределенную случайную величину: количество людей (из 800 опрошенных), сказавших, что они собираются голосовать "за". Если предположить, что мнения по этому вопросу разделились поровну, вероятность того, что каждый из опрошенных ответит "я — за", равна π = 0,50. Найдем теперь среднее значение и стандартное отклонение величины X, воспользовавшись для этого соответствующими формулами для биномиального распределения:

µ_х = nπ = 800*0,50 = 400

σ_х = = 14,14.

Теперь, чтобы найти вероятность того, что Х принимает значение, равное по меньшей мере 437, увеличим пределы на 1/2 — при этом надо будет найти вероятность того, что X составляет по меньшей мере 436,5, и можно будет воспользоваться тем, что распределение X приблизительно нормальное. Итак, нужно найти вероятность того, что нормально распределенная случайная величина со средним значением 400 и стандартным отклонением 14,14 превышает значение 436,5. Для этого нормируем значения:

z = (436.5-400)/14.14 = 2,58

В таблице нормального распределения находим, что в предположении равного распределения мнений среди населения вероятность того, что интересующая нас величина достигает для рассматриваемой выборки граничного значения (или превышает его); равна 1 - 0,995 = 0,005. Правдоподобие получения такого результата очень мало, вероятность составляет всего лишь половину процента, что соответствует 1 шансу из 200.

Вы задали вопрос, что будет, если мнения по интересующей вас проблеме разделились среди населения поровну, и получили на него ответ: "В таком случае получить в выборке результат 54,6% (это 437/800) или более, очень маловероятно". Таким образом, использование сценария Что если? дало возможность опровергнуть предположение о равном распределении голосов "за" и "против" среди избирателей. Это неплохо для начала!

Распределение Пуассона и экспоненциальное распределение

Существует много других распределений вероятности, которые полезны в статистических исследованиях. В этом разделе кратко описаны два таких распределения и показано, как их можно применять в конкретных ситуациях деловой жизни.

Распределение Пуассона

Распределение Пуассона, подобно биномиальному распределению, связано с подсчетом количества наступления некоторого события. Отличие состоит в том, что в случае распределения Пуассона нет заданного числа возможных попыток п. Вот один из примеров возникновения такой случайной величины. Если некоторое событие происходит случайно и независимо в каждой из попыток и среднее число наступлений события с ростом числа попыток не изменяется, то коли­чество наступлений события в фиксированном количестве попыток будет подчиняться распределению Пуассона. Распределение Пуассона — это распределение дискретной величины, которое зависит только от ожидаемого среднего количества наступлений события.

Приведем примеры некоторых случайных величин, которые могут иметь распределение Пуассона.

1. Количество заказов, которые фирма получит завтра.

2. Количество людей, которые обратятся завтра в отдел кадров компании.

3. Количество дефектов в произведенной продукции.

4. Количество звонков в фирму в течение следующей недели с просьбой помочь разобраться с “простой в сборке” игрушкой.

5. Биномиально распределенная величина X при больших п и малых π.

На приведенных ниже рисунках показано, распределение вероятностей случайных величин, имеющих распределение Пуассона, при ожидании в среднем 0,5 наступлений соответствующего случайной величине события (рис. 7.5.1), ожидании 2 наступлений событий (рис. 7.5.2) и ожидании 20 наступлений события (рис. 7.5.3). Обратите внимание на то, что форма распределения Пуассона, показанная на рис 7.5.3, подобна колоколообразной форме нормального распределения. Это свидетельствует о том, что в случае ожидания наступления большого количества событий распределение Пуассона приближается к нормальному.

Распределение Пуассона имеет три существенные особенности, знание которых позволяет находить вероятности, если известно только среднее значение случайной величины.

Для распределения Пуассона:

1. Стандартное отклонение всегда равно корню квадратному из среднего значения σ =

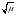
2. Вероятность того, что имеющая распределение Пуассона случайная величина Х со средним значением µ равна а, выражается формулой

Р(Х=а) = , е = 2,71828…..

3. При больших средних значениях распределение Пуассона близко к нормальному распределению.

Пример. Количество возвратов товара по гарантии

Фирма работает с товарами очень высокого качества, благодаря чему каждый день ожидается возврат на гарантийный ремонт (в среднем) только 1,3 единицы товара. С какой вероятностью завтра в гарантийный ремонт не поступит ни одного изделия? Какова вероятность возврата одного изделия? Двух? Трех? Поскольку среднее значение (1,3) очень мало, вероятности необходимо вычислять с использованием точной формулы для распределения Пуассона. Вот эти вычисления:

Р(Х = 0) = е^-1,3 * 1,3⁰/0! = 0,27253 * 1/1 = 0,27253;

Р(Х = 1) = е^-1,3 * 1,3¹/1! = 0,27253 * 1,3/1 = 0,35429;

Р(Х = 2) = е^-1,3 * 1,3²/2! = 0,27253 * 1,69/2 = 0,23029;

Р(Х = 3) = е^-1,3 * 1,3³/3! = 0,27253 * 2,197/6 = 0,09979;

Зная эти основные вероятности, можно сложить вероятности возврата 0, 1 и 2 изделий, чтобы вычислить вероятность того, что в гарантийный ремонт поступят 2 или менее изделий. Вероятность такого события равна: 0,27253 + 0,35429 + 0,23029 = 0,857, или 85,7%.

Для вычисления этих вероятностей с использованием Excel применяется функция- =ПУАССОН.РАСП(значение; среднее; ложь), которая вычисляет вероятность того, что случайная переменная, имеющая распределение Пуассона со средним значением µ, принимает некоторое конкретное значение а , а также функция =ПУАССОН.РАСП(значение; среднее; истина), вычисляющая вероятность того, что значение имеющей распределение Пуассона случайной переменной будет меньше или равно значению а.

Пример. Количество телефонных звонков

В среднем в фирму поступает в день 460 телефонных звонков. В предположении, что количество звонков подчиняется распределению Пуассона, найдем вероятность того, что завтрашний день окажется перегруженным, т.е. телефонных звонков окажется 500 или более.

Среднее значение дано в условии. Стандартное отклонение составляет 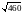= 21,44761. Поскольку среднее значение достаточно велико, для данного распределения можно в качестве приближения использовать нормальное распределение. Нормальное распределение — непрерывное, любое значение, превышающее 499,5, — будет округляться до числа 500 и более. Нормированное количество обращений равно:

z = (499,5 - 460)/21,44761 = 1,84.

Воспользовавшись таблицей стандартного нормального распределения вычисляем искомую вероятность: 1 - 0,967 =0,033. Таким образом, вероятность того, что завтрашний день окажется перегруженным, составляет всего лишь около 3% (т.е. такое событие не очень правдоподобно).