3.4.7. Обчислення об'єму тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями:

а) 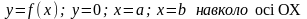б)

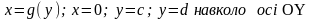
y y y=f(x) x=g(y) d a b x

с х

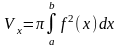
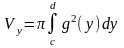
Приклад 3.

Обчислити об'єм тіла, отриманого обертанням довкола осі Ох фігури, обмеженої лініями:

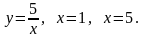
Рішення

Змалюємо на кресленні фігуру, об'єм якої потрібно знайти.

Оскільки отримана фігура обертається довкола осі Ох, то скористаємося формулою

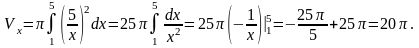
Приклад 3.

Обчислити об'єм тіла, отриманого обертанням довкола осі Ох фігури, обмеженої лініями

Рішення

Змалюємо на кресленні фігуру, об'єм якої потрібно знайти.

Оскільки отримана фігура обертається довкола осі Оу, то запишемо рівняння лінії у²=4-х у вигляді х = 4-у² і скористаємося формулою

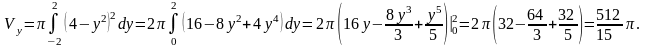
Змістовний модуль 4 Диференційні рівняння

Тема 4.1 Диференційні рівняння

1. Задачі які приводять до диференційних рівнянь.

Диференціальні рівняння виникли із задач механіки, в яких брали участь координати тіл, їх швидкості та прискорення, розглянуті як функції від часу.

Задача. Швидкість тіла, яке кинули вгору з початковою швидкістю 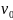дізнається із рівності 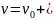, де t – час, q - прискорення руху тіла. Знайти рівняння руху тіла.

Рішення. Так як 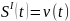, а 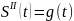тоді підставив в рівняння швидкості отримуємо:

Отже щоб знайти рівняння руху тіла потрібно розв'язати отримане рівняння відносно функції S(t) . Таке рівняння зветься диференційним, тому що містить похідні або диференціали шуканих функцій.

2. Основні поняття диференціальних рівнянь

Рівняння вигляду ,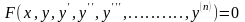

що зв'язує незалежну змінну х, шукану функцію і її похідні різних порядків, називається звичайним диференціальним рівнянням. Порядок n старшої похідної, що входить в запис рівняння називається порядком диференціального рівняння.

Приклад. xdy=ydx,

Рівняння, що містить похідні або диференціали не вище за перший порядок, називається диференціальним рівнянням першого порядку.

Вирішенням диференціального рівняння називається функція, яка, будучи підставлена в рівняння, обертає його в тотожність.

Процес знаходження вирішення деякого диференціального рівняння називається інтегруванням даного диференціального рівняння.

Загальним вирішенням диференціального рівняння n-ого порядку називається таке його рішення

яке є функцією змінної х і n довільних незалежних постійних . (Незалежність постійних означає відсутність яких-небудь співвідношень між ними).

Приватним вирішенням диференціального рівняння називається рішення, що отримується із загального рішення при деяких конкретних числових значеннях постійних . Задача знаходження приватного рішення диференційного рівняння зветься задача Коши, задача Коши окрім диференційного рівняння повинна мати початкові умови.

Приклад . Розв'язати рівняння xdy=ydx, якщо при х=0 у=1