Тема 3.4 Знакочередующиеся ряды.

Под знакочередующимся рядом понимают ряд, в котором члены попеременно то положительны, то отрицательны:

u₁-u₂+u₃-u₄+_…+(-1)^n-1u_n+_{… ,} u_n>0.

Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине u₁>u₂…>u_n>_… и предел его общего члена при n равен нулю, т.е , то ряд сходиться, а его сумма не превосходит первого члена S≤u₁.

Пример. Исследовать сходимость ряда

Решение :

Так как члены знакочередующегося ряда убывают по абсолютной величине и предел общего члена , то по признаку Лейбница ряд сходиться.

Определение 1. Ряд называется условно сходящимся, если сходиться как сам ряд , так и ряд, составленный из абсолютных величин его членов.

Определение 2. ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Упражнения:

I. Установить сходимость или расходимость ряда с помощью признаков сравнения:

1) ; 2) ; 3) ;

4) ; 5)

6)

II. Исследовать сходимость ряда с помощью признака Даламбера:

1) 2) ; 3) ; 4)

5)

Тема 3.5 Степенные ряды.

Перейдем к рассмотрению рядов членами, которых являются функции, в частности степенные функции

с₀+с₁х+с₂х²+_....+c_nxⁿ+_{… .}

Такие ряды называются степенными, а числа с₀,с₁,с₂,…,c_n – коэффициентами степенного ряда.

Пример: найти область сходимости степенного ряда

1+х+х²+_…+xⁿ+… .

Решение:

Данный ряд можно рассматривать как геометрический ряд со знаменателем q=x, который сходиться при │q│=│x│<1. Отсюда

-1<x<1, т.е. областью сходимости является интервал (-1;1).

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Теорема Абеля. 1) Если степенной ряд сходится при значении х=х₀≠0(отличном от нуля) , то он сходится и, притом абсолютно, при всех значениях х таких, что │х│<│х₀│. 2) Если степенной ряд расходится при х=х₁, то он расходится при всех значениях х таких, что │х│>│х₁│.

Из теоремы Абеля следует , что существует такое число R ≥0, что при │х│<R ряд сходится, а при │x│>R-расходится.

Число R получило название радиуса сходимости, а интервал (-R; R) –интервалом сходимости степенного ряда. На концах интервала сходимости, т.е. при х=- R и х= R, ряд может как сходится, так и расходится.

данное выражение позволяет вычислить радиус сходимости числового ряда через его коэффициенты.

Замечание . Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку (R=0) , у других охватывает всю ось Ох (R=∞) .

Пример. Найти область сходимости степенного ряда

Решение :

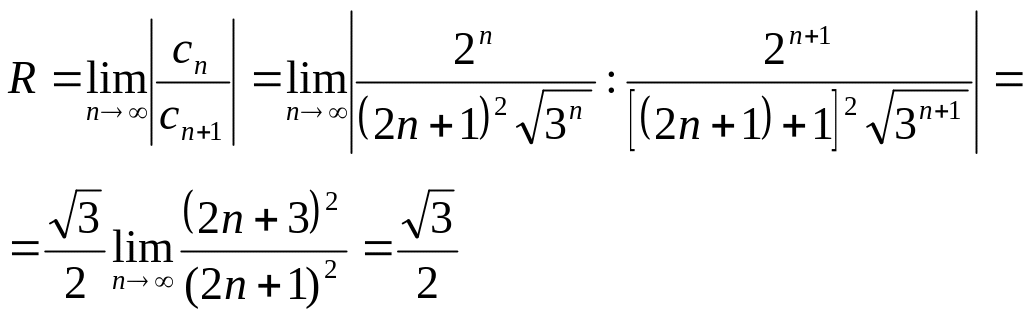
т.е. интервал сходимости ряда .

Ответ: R= .

Сумма функционального ряда представляет собой функцию, определенную в области его сходимости. Про эту функцию говорят, что она разлагается в данный функциональный ряд. Для степенного ряда сумма обязательно будет бесконечно дифференцируемой функцией внутри интервала сходимости, поскольку степенной ряд можно почленно дифференцировать, т.е.

S(x) = , то существует S^/(x) и верно равенство

.

Это одно из замечательных свойств степенных рядов. Из этого свойства, в частности, вытекает, что при фиксированном х₀ разложение функции в степенной ряд единственно и имеет вид

Указанный ряд называется рядом Тейлора.

При х₀=0, рассматривается частный случай ряда Тейлора- ряд Маклорена:

Элементарные функции е^х, sin x, cos x, ln(1+x), (1+x)^α разлагаются в ряды Маклорена в интервалах

e^x=