5.2.2. Эластичность функции

При исследовании паутинной модели рыночного равновесия одной из главных является задача о том, насколько сильно изменяются спрос и предложение при изменении цены. Другими словами, требуется оценить чувствительность спроса и предложения к изменению цены. Для измерения чувствительности одного экономического показателя к изменению другого показателя используют относительные изменения переменных и .

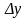Пусть величина непрерывно зависит от , и эта зависимость описывается функцией . Изменение независимой переменной ( ) приводит к изменению переменной ( ). Предел отношения относительных изменений переменных и называют эластичностью функции . Обозначим эластичность изменения переменной при изменении переменной , тогда, используя определение производной, получаем

,

где – предельное значение функции в точке , 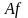– среднее значение функции в точке . Эту эластичность называют так же предельной или точечной эластичностью.

Замечание. В экономике под эластичностью понимают отношение относительных изменений переменных и : .

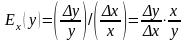Свойства эластичности

1. Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины и : .

2. Эластичности взаимно обратных функций – взаимно обратные величины:

.

3. Эластичность произведения двух функций и , зависящих от одного и того же аргумента , равна сумме эластичностей этих функций:

.

4. Эластичность частного двух функций и , зависящих от одного и того же аргумента , равна разности эластичностей этих функций:

.

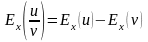5. Эластичность суммы двух функций и , зависящих от одного и того же аргумента , вычисляется по формуле

.

5.2.3. Использование эластичности в анализе экономических показателей

Пусть – функция экономического показателя от экономического показателя (или фактора) . Различают три вида экономического показателя в зависимости от величины :

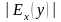а) если 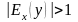, то экономический показатель называют эластичным по ;

б) если , то экономический показатель называют нейтральным по ;

в) если , то экономический показатель называют неэластичным по .

Эластичность функции показывает приближенно, на сколько процентов изменится функция при изменении независимой переменной на 1%. Если экономический показатель эластичен по , то при изменении величины , величина меняется сильно, а если неэластичен, то слабо.

В качестве классического примера абсолютно неэластичного спроса ( ) рассматривается спрос на инсулин, неэластичного спроса (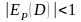 ) – спрос на товары первой необходимости (хлеб, молоко и т.п.).

Найдем изменение дохода (в процентах) при увеличении цены на . Величина спроса численно равна количеству проданных единиц продукции, то есть . Тогда доход (выручку) производителя от продажи единиц товара можно вычислить по формуле . Используя формулу для эластичности произведения функций и учитывая, что эластичность спроса по цене всегда отрицательна (зависимость спроса от цены – убывающая функция), а , получаем

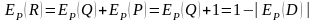. (5.1)

Из формулы видно, что эластичность выручки по цене отрицательна для товаров, спрос на которые эластичен ( ), и положительна для товаров, спрос на которые неэластичен ( ). Это означает, что если спрос неэластичен, то изменение цены вызывает изменение выручки в том же направлении. Продавцам выгодно повышать цену, так как повышение цены увеличивает выручку. Если же спрос эластичен, то увеличение цены вызывает изменение выручки в противоположном направлении. В этом случае продавцам выгоднее снижать цену на товар.

Пример 1. Пусть опытным путем установлены функции спроса и предложения от цены товара : , . Найти: 1) равновесную цену; 2) эластичность спроса и предложения при равновесной цене; 3) изменение спроса (в процентах) и изменение дохода (в процентах) при увеличении цены на 10 %.

Решение. 1) Равновесная цена определяется равенством или 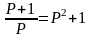 . Решая это уравнение, получаем, что равновесная цена 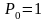(денежных единиц).

2) Найдем эластичность спроса по цене:

.

При . Так как , то спрос является неэластичным по цене.

Найдем эластичность предложения по цене:

.

При . То есть предложение по цене нейтрально.

3) Найдем изменение спроса (в процентах) при увеличении цены на 10 %. Так как эластичность спроса показывает приближенно, на сколько процентов изменится спрос при изменении цены на 1 %, то при увеличении цены на спрос изменится на величину . При получаем , то есть спрос уменьшится на 5 %.

Найдем изменение дохода (в процентах) при увеличении цены на 10 %. Согласно формуле (5.1) имеем 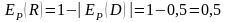, тогда , то есть доход увеличится на 5 %.

Ответ: 1) равновесная цена (денежных единиц); 2) при равновесной цене , ; 3) при увеличении цены на 10 % спрос уменьшится на 5 %, а доход увеличится на 5 %.

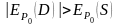Замечание. Используя значения эластичностей спроса и предложения по цене в точке , можно выяснить, сходится ли последовательность цен к равновесному значению. В частности, если , то последовательность цен сходится. Если же , то расходится.